Distinguishing Risks of Modes of Cardiac Death in Heart Failure with Machine Learning

In medical fields like cardiology, the Wolfram Language continues to help researchers make discoveries and predictions. I recently coauthored a study that uses the machine learning functionality of the Wolfram Language to predict risks of deaths due to heart failure. In it, we aimed to build a classifier that is capable of distinguishing the probabilities of cardiac death caused by end-stage heart failure (HFD) and severe arrhythmic events/sudden death (ArE). What follows is a summary of the paper we published earlier this year.
Reliable risk stratification models are coveted for selecting appropriate therapies in the treatment of chronic heart failure, a serious health problem in current aging societies. Despite the substantial progress in pharmacological treatment and various devices, the mortality rate is still high. The therapeutic management of high-risk patients is also very difficult and costly, involving implantable cardioverter defibrillators and resynchronization therapy. With these concerns in mind, we studied the applicability of machine learning techniques, with the help of the Wolfram Language, to distinguish the risks of HFD and ArE in patients with chronic heart failure.
Significance of Each Outcome and Important Parameters
In the supervised learning we have implemented, the inputs are comprised of 13 clinical variables, such as age, sex, severity of heart failure (functional class defined by the New York Heart Association), etc., and the output has three classes, namely: (1) heart failure death (HFD); (2) fatal arrhythmic events (ArE); and (3) survival (alive) during a two-year period of follow-up.
When a patient with chronic end-stage heart failure dies, it is classified as HFD. In such patients who are typically elderly and/or associated with heart diseases, the pumping ability is deteriorating and the ventricular ejection fraction is low. Deaths due to ArE consist of sudden cardiac arrests and deaths, and also include appropriate functioning of a defibrillator against life-threatening arrhythmic events, because an irremediable consequence must have been inevitable without the therapy by defibrillator.
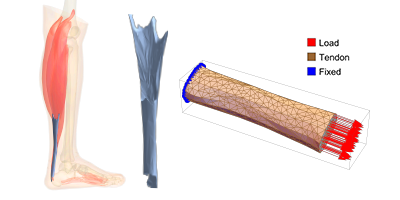
Let us briefly describe 123I-metaiodobenzylguanidine (MIBG) scintigraphy and an index obtainable thereby before showing the result. It is one of the diagnostic tests in which radioisotopes are labeled to substances that accumulate in a specific organ and the distribution of gamma ray radiation is detected to form an image, i.e. a scintigram. Among other things, it has been found that the heart-to-mediastinum ratio (HMR) calculated from 123I-MIBG can be a useful indicator for cardiac mortality risk, when combined with other clinical parameters. Therefore, we want our classifier to be able to show distinct probabilities for the three classes, i.e. HFD, ArE and Survival, as a function of 123I-MIBG HMR. Nevertheless, the HMR alone is not very useful for our purpose, thus 12 other parameters are incorporated into the set of predictor variables.
The HMR is calculated as the ratio Ch/Cm, where Ch and Cm are the mean pixel values of areas corresponding to the heart and the upper part of the mediastinum, respectively, in the 123I-MIBG image. The mediastinum is, roughly speaking, the area surrounded by the two lungs. Since the edges of organs in scintigrams are rather blurred, it is in general hard to select the relevant regions and compute the pixel values systematically. Following is a quick Wolfram Language app to facilitate the region selection and automatic evaluation of the HMR as well as other indices. This may be widely welcomed once further improvements, such as automatic region selection, are implemented.
This sample app provides a GUI, with which one can select the regions corresponding to the heart (circle) and mediastinum (rectangle) in the given DICOM image, and the results of calculations using pixel values in those regions are simultaneously displayed:
 Engage with the code in this post by downloading the Wolfram Notebook
Engage with the code in this post by downloading the Wolfram Notebook

✕
img = \!\(\*
GraphicsBox[
TagBox[RasterBox[CompressedData["
1:eJztvdmSI1mSJaZYDQZbsAO+u8eWsWRm5L5VZVZ2VS81PS9kD4UfMBQ2h3xp
ivRQhMK/p91zjppeeNZbomVe7LpEOByAA3BTvbocPar3xf/2f/+X/2NsZv99
0f33X/7r//vnf//3//r//S+b7of/9d/++//13/7tX//3f/63/+df/9u//vtX
3/+f6Xk20r9hDWtYwxrWsIY1rGENa1jDGtawhjWsYQ1rWMMa1rCGNaxhDWtY
wxrWsIY1rGENa1jDGtawhjWsYQ1rWMMa1rCGNaxhDWtYwxrWsIY1rGENa1jD
GtawhjWsYQ1rWMMa1rCGNaxhDWtYwxrWsIY1rGENa1jDGtawhjWsYQ1rWMMa
1v+ANfobt/xnDpQf65b1P/Mr3Tvpvk/1/9hmus3H+Mw5/p90X6Pseel7+ppZ
gd+ad//PdN8EX+n7XPdMu2ct8PNM75J+a47fn+o3Z3qNsb4Xumfe3eI9M/12
eix9ogU+z0ifaKR3LvRp07vxsTk+Tfp/pr9hgt/wTznBs87/zXAvv+b6Hb5a
uiq8knGdnn9Z/6z8yl96jTOZxn0jvbdrAOU/yeRu+ivm+CtLXOP0Ny9xT6nr
NcP1mug68aqna7HsnlFY3X3NrLKmuyf9X3Vfq+77Uq+QrvQMEqJW1N3jZffV
dPctrcWt2ta2725tun+77va6u2+D12j695h3r7rtvjfd79Td7WX3L+nDGq9W
SzPK7ucpPt+i+7/t3muOd6rxqebQoQkeT59+Io0tIf0KP1X629PVqHEFSvxW
gb9v1r0K32sJ/XJNmPbSHWdScB0Z91IZ6bpfdk177cr1wD/LONMCflaDTNJ1
sH4vcC+Nu2vlu6vq7lni+lSQ3ELyXOLapCtUQXcW3b+6u7eC3lS43pRIi5/X
em6FZyRpLiDRNWRSdlJN95+672vJ96jnTPGcdHtnh+52uvZt94yVdDVpT5Jz
hZ9n3SPj7tYSf0sDS1NAV2rpY4v359cC0ixwzxz6yb+KdmsE7Vx0n2mB59T6
i2k7Ftonbjlc9rkUwjK4/XVN+I+wAP4O3OXTM/vjj4edn/RWfIJdMJUNmMsW
z3Gr0I6i7qcdM9EjU+ys0I4FrvoC8thmO9t1YoqrvMQ9Je5pINckmx12+arb
/8fu9gZ7fIVrvYXEajyzgU1pcavCTzUknPZri2cX0EH3QCU+QYFP0OATUtYN
ZMZPk/zGQraOf1WSVgENn0sraEna7nMV0I90DUtZGPoDXsVxf33/1jU3G5/J
6ZIrbH/cDr/k97s+jLN/hs+dfONcf/cEf/dUe3zaX4ESV6OA7Siw53gFCvkA
l2yNq73U1a9lF2r5iDmua9pTJbyFP1Z1ct9DA3a40hUkm15th+ue5J5+5wHP
X3ZfG3iI9Lvc+wtp1Rzv0fafaA75p8cb2JYSf2WB/csoYqn7JnhHPlrCR8yk
CYUiEeoDPUWB/6kxpngjpM59Psluh/+99O7PbX3+PZf/BP/P+mfk/9ObTxTZ
uTXnjqCUK+ymmTRgLvnP5QloT2vskQZSbWQLanj0QrJs8BpLXf20Zxd4tIIn
38P2p12aLH+yAa0k3MCj03snW1F1jy7x8xb+ZCErv4A9avH50q7eSFNpHWrZ
jBY+vVAsWeF/t3pzfO5k0Rr8hQt82jVer4asS8UP/A2TXkz6OPI8xst3WW4V
zC5pBf7WK+cR56jXzKnlNmrSf7qxYro5rk0FG7DsLTav0RJ/a4urUilCYkzf
aI/x6vNKr/Gd8dMaj7WQxRLX3vcYo8YaO3PXef8ru8buP3bakHb9Bp9g20kt
xYbp3wE+IFmDPeQ5lWyK3gLQr6+hj2tIn3FIg+8L2P8Cf88S775QVFAoM2Ek
SB8zw7WpoOslfMW8z0DC8vNK8/u833Ehk/MdH/nX+GIa8NtoMyKNPCaZ9Fox
xk8T7fd5n5+NZPMKXFtq/BTXiHtlin1NG8F8YQn76Za8gO1dwX9vEMeX8AYr
7OSFvEmBa1dgX5fYz8kCHLt7D/itTacHlfQsxWu8dwcrkTSlxuvtZfsrvPsU
Oljg+WX3+EI2p4DkS/g3ynAp31PiM8wU7ywURc6lQ4yBGBuW+NyLPvebK1Mc
IW4eZxLPpR0RQG6JPT57Hin+fg0Y9bfGsjfc+aZoPzRzAs12bfD8eqTcjlnQ
vPfvHvMWioDpD3jtC+jBoo/+CmnEGlJPV3PTSaSFbyhwH73tGvvS84Q18r6V
3XSyPUJrttj79AEb6NS2u3/bPXrsbh8QYSYtmEHvml5fqYUNrLxnHKV0o9Jn
qvVXzfF4ev5Ynm6m3b7Qnl/ir2OWu5DnK5Q/mqJ+z6OnvU0dZdKY9HKO6Cu3
zJeU/9jOdW0ki5S/n2d+zPhMmjLWXudfUiryWSjeZd5XSbb0EO75V31EN8UV
b7RvPcPnFd4qz6shbe7pBR5dS59a7PCU9V13XmDT+YKkDxXiwRQNXkOy6d49
9KCWJ2LEUWpnL3C7BSqwlCTnsAYrSdxju7Uy1lb2YqF4n39vAa82U25JFMGR
rYWu1Ej2P13PWX/9I9Z3XZj093gkENpxGRQgNGxi4V38vfLsM2KD8Pvj/nsh
lIyxL216ozi3kuWuITnuigo60ECilOYMtoBaUBqxl0r7rFSOlsdPtSxr0otV
J+ObTvYP3b+T3fbZftv9vOte8YDbu+6Rq05L1pDbHL/PPKPGKxNfoEa20IEZ
nlVA5iVQjGXvAWjpqe2e61Xa/QvtgVLR0AKfuxFGMpU+jIWCzjPr6x74HPvz
fWmWx4WXWuf+5DnK6PGfa6X1noH6Sw1wBHcCzZ5LVkvdP5bmM8abK8pe6kqE
D62kE3PY9C1iwQb7b40MrlS0VsJKlL00NrABydqn30p+/gSrn5DAJfY9vcAd
okGP/ZdCHZdCdxaK8so+rpwjFpgBVwwLvlAsQ/Spli1YyM5R8hNJvuhR7LFy
nhzbnuuqhrynWabv/z/H3UM/LrfOUehzvIH3zCz3Q7ReI9l9RnOO3dOjc5dP
tYOnyvBn2A1LXPM54vumz6GnsLaUJ23CFvpyRDzY4ncmtpSFZma+gmSX2O1H
+PYb5IAphqefJ4K7QjZZIztcQ7JV/xpL4YlL+IBaP1O7iN41kCxtVqWopRbC
x1xlob9sbVFj4L18naWin3SdRpK/mVdMclQl/PBzmY/7fXdZuT+/RX30CC+y
fsf7PW6x/nn+txTC/pgNMyteCIElXsbsiR6zwbVaysJX8B5LZfxzWPUWfrwW
YrOQT2gQadV9ZNAI9dl28r/p9vhO6F6LGCB5gtvu/xbRP/f2Kqsz0Ku3+rQb
m8ur18Yqw1Z54lz+hnt6IWtALLBWjL/QM2vFAIWwj4WiiWTpF7L5k14PznHe
HHkN2zC28ZlmXFb+tEYu+7A2ue/JkajwTI5fMhvid4/3ZpD7Qlekkv1eKDtY
YCcnvKDukbZCPqEAAkPcjv6dOH+jWHwplKZWrr1GJL6Gr/f4v9ZeZqXn2Hn+
BvqwxTvXeJ2ZfA13sX+CBq9XKNNo8a61fDq9D/XXtSDpwEgx/gLxTnqtsXLb
heKZUjjJTN5gatYjv4G1nGO+k14KcdVz63wpDYjd7O87yX4OeYddOtfUsXY/
//qF9nmleLlULl31e2Sm+Ivya/B4KxmspREtrnmFvDFJg3vW5cL8YoX92eA5
xP53kH0jjaDG7BCpJ6/C6k/dZ4+sCjD23/bWnM+qpFcNkJ6pPDzth1fzdspA
KmWFE1v2dY6i12TiX3PI23fJ1KbK+yKWcgzV7x31j4RPzmPxS0k/XuscaSTq
53Z/bKaYlZ9kJj31mjtRoJns4gpXaWGO3xL7XvTasZJtXML2trD1yWdPrFTF
Zqqd3/Q7u4GUavl04i0V5DZVPriS568VcWyV321RC1gDBarljQp5m6Uy9Uqf
h7WnRrIj0t/g56VyxKU8lMeJjv64j58p4omMv8Sn8Xo2rf4UGjHPdplbefex
sQfzWPDya5x9AteD3Co99/6hiePegk2l0wvZxKmi/EJyZw28FpY76+OiQIHq
HjdYZDlfi924wU4r5ZUb7OpJ75Mr6AnR2YX+1ard04bMIX9KtpIONsLpK8io
7X18gdyD/qvp93IlJGqB92PESRbADEgSkd25spk5IswSu4NY4VTR8VI+oLCJ
Yv3nUdbIohrgezR//LL4T55LnteC8pxjpB0f9n7UW6sRsv+5/lbGd+R9eD2M
EuWu8arYHLaV9R/KY6m8bo49z73XKldYyCMvkIltFJ/PJc3WnD/gFmYtnUu+
fqesctl7jEqIBHPJWu9On75V/knseQH70vT5gDNPWNmplDvSjkzMccFCNmGp
3V5K2lPz6ugcOVOBa+Z5NK/sJJOCV1n8ds64uew6j/oCfwwvNO0RKUetyegJ
BtgSV4D+eab9OdMObSVPr5pM+kyZdpPxIX0646jGKuV2NaRWa18vgQPsseML
xWul4oymt8PUHOb5KbKY9j57jleZ9vma53ULeYJSyB0f3UK2Uz2zUi1ojmfW
+gsikyyQqVLbvco5g3bOZfMrYeTzPp4fP9vZLvFxL2dKfZLtd+rJpfC/iZ0j
ixHtOQvEzj4F431+n/axycjI5SuU25TKARkdO0pHXL3AKzjiT3+5g5RpWVfC
+tOtia51JbS1RpxQ6t41NKfE79K/LBQlNorwC1gB1vRpKyrZorW8tUd1jfY3
PcxK7zJXJlpAp9xWFNr3xHyminfWsm61MCKvVxfy9uk1ptA1w89jCzZNnvl7
NO5ReI7L5BpwmeVoTo4tBc4wkWePOMTjQJf/RPo9FhbqbE7iuDNF9QtZy1Ie
32upjqPMtI9q7M5Su72BN1jZopfbBvey8rrGtWVtdi4tKWHDaQdq5AkL7MCV
sZbje3VmjvwuFK+t5LlYBVjidzaIOEt5qRpasRSzoJDmUgc2xorgHH8f7c3c
nJNKbWBsv1AGEAhajqznPj5HfvwZUQm8zMoZP7+NLPyT5PzAqbTVNWGiv5Ks
XCK6biOXipG9dkv+o8tgLjxtalNd4UZ1nkLZ+ULZ+Qw7h8wext4b7V164ErW
glXCJI+xVars1crVS1mPUt5/pnihUMxYKyKogQWRbbiT9lTCBwvoDGsELbSJ
foua7h6G+u2ckMZm5jwo0+4IrzmRX48rHLKeZPvQ5ZL75EusvJoULB5HIyba
6a55s7PP5zUjR/29/uXZ3lIxG6Oe0or+Wq1gt8mn4hfrqnvk3IVqfM75Sjpy
NFbmiSrV+m3nhHrtYNXHXvQLNXBjZxestV+3eM2dNfIXE2hKLXvg/KK5ZL4x
r0bydVfKD1jdcK4qYx5amEK3PJohYsyq90QR1AzXLXhfeYXdZT61fNdPelld
GvuP/G/8zA441+Nc/0Ifnbs0VVTrFQBnSDFDGiOScyy4VdTNvcJc3Tlfix7P
Wxi5n2s90uDa0+ey5kN7scE/r9mxwjSVP2nMq/FLyYuxxbSPBgrhQAtlhAXs
O5HnxrxGVMFX7BT5O1JJlulSOkU+WqmYZq5stsnuWwj7Y77EqrmZ9Qgqr/vU
LNv1415C8X3Wy+xS0o9dn9cYXcK5PniuOsn0ZaLcwHcy/d3SvO9hgevt3Cqy
PWvl7a3kOJMsdkbEr9Q15m7eCidcyJ6QXTXD9Z8qeyyB7jXK6iewIss+dixk
azy6q2TFS7zz3NgPwKhuryzmYAtFnJ6X0hNM9IpE+IlUFDaX5pZW9brMmvUS
V8B7UWhTyfwby6J6dpXvqhxvzfs/fhsb/N6Ve4B43XP8Nyo+Hpn6bzmOORf6
4Zn7FDGZZ0fcca2x38Jz+uCBtbq2jax2rcx+JYtAGZCXV2pHb4HvbhGfUb5T
xGHuoRvZ+Tle37O7pdCDLTKAVlZmh99xNLLobQ4R/KU5bsm/ZqZolf8a5ZL0
9IwTiR55BOBIyFReIhDASZ95u50N9u3EzqM8asI0++kSa3wm6dzPRH1nas99
BGPCsWwX9dn7rkyWlrkAa2OVJOhZ90y+YKEMgdEgsRfP5Zm7JXt9kARocVsh
R61Vqu7X5tXamRGhXWnH1ooa5sjQGG14BrIUjkg7PVdsmGz/VBZiowxwKjuw
wLs3tuxtS6OMl1hPpeiP/HbPjWbSclZHZz1SOlEkfZ53m50zLX7r7S/N/uA7
jnuNy2OQ8AI5Ozw8hne/OfJL+8Zerbn2d4mrxryIjIha/rU29l8Qc2nkX7fm
mD5ztq0RGVopFqsVA7ASnJg+9M9bY/XI84vkkfewIa28gGOA2z7iqGFVNtrd
Ln9qRmIMtPI3Sz0yV5xPm04uEn2d1yCSl6DUi17XS3PWEiuG3DPeZZizvvIK
YG7zz5F415pLrNjreUzxHBHOn+lIZLDAnPs8RVwTuTyZfenKjbUbaanprxvz
PqqVReV8C+9dd/F+CV1gFW+u2GzRR/8b5RHEY9nxRzZPqb26kD0vpQ2sCays
6rNRosK1stJG+M5cWMAaOrXA7xCBrBXH0nospIUeZzoDYKp8glFfKd9I78Tn
eM43y65waEBwgHJvHFL6Wzbh98jf/59kWhaPBg+I2Wv+iUfKXB33Y6w3632l
93yw/tnIPs6E5yyU/W+wP3bCCVrdWwsBXijuK5Wt0S4nuV3DojTq6qzkzymV
WpIl22upyHCmyCAksVAs572iK1iDK9irBtXkFT7vCn8LEYJS2UPZ57kr5T1T
xTreSTA37ykqlMsS9x8LAXBrarKiZoGw5l1WgRSbXRr/yXPK39b2ohrltj/P
SD1uHfcYEKM5ZjpT+XWPiWaKkZkBjGXFWSHm1S+E2bK3c4qdR5SXESEtRYXM
fWG19mQDGa8R+TV6NfJseN2XfcTP9/Zcj9YhxfMtNGdllXxMA4nvrexjQ+b4
KysVfy6FEi56e1P3mIdLvZXuN8r9iffObGaO7bjHdR71eX0v9mfs0ed79lI6
kPd75PWA0L/oRBoL9Xf/PwbuSfav5/2mCMj7YudCbYnpVUBilrpW9MKbni/t
EQNrhAW6eVbSkR3ycEpr27PDGkmwRfZGm0HMuZXFWJuzyltVlBb4namqSK2Q
v4Oyhz10bgU+KfFl7/Lh/i+FVFJrV+b94B4VbLETGC/WuBKeD/hcgql53+95
lTUQ3lzSYQX80emF8P+wJrmlcQZAXgeOSDC0YpppL2s6RPRZJXNEJN0/EYLj
3VaM0Q6Ivyp1aTA6IM+XNRpa3AUitlaSqMHgXktqrBgRFyLj21kGZA4UkBxz
yUqvOxIKVSsLqbrPcYDst9j5S/CFK/QKLHBfleFBbZ/Tl/JI7CQnp6E2r29M
lW9U5pXm8IYTcxw9Mn3PrXKsP/Rj0mdhl2Z/5ahz+B2PUXLs51wz3GZQq30u
RiH8ixYgeuXZW90qs2OdjajcRvJeYbdzN5fY3432N+1D1fuGlBE2kPYWFmEF
hsgKMWArq1JITitjdxe9QaVMz+sC7AtfCkdg5yi1K3WTn8w7z0poKCsWXsdi
LWCGbHEqpMA7QSvltsSAeR3Y90v7GJNR8n2VSyCPxfLMMOz+1C6zvLrH1/Rp
FOEBXB9GFrw0rwDzPrdoc2FBrHey293xU4/wp+YdlK0tFemxUnMwdoNUssE7
2IIaUp6B1V+hf+uoXq4K1jk9fgUrveiR443sfWHOvCxg6/fSP7INyd8jj3gl
C7HB176TPCdJcGYINWOhCKLtmUBe74lZJgvJ3rvH5siIyHiM/oG5ef0/UF/H
WUbmPnhypgHn+eDl+z+oCeeVpvMoJJf71Ga9/M/72Wey+nNzfkdjrA157ddR
ALL5W91LjvTWfEIHfTy5Oyv44626vJaw0RW8B/tDtqoK7807QhiT+TwZ+u9G
OEAhu9JAnzZ4xwPec4tuoZ28/wHWgDa9wfN8cggjhrkwpFIYQJnhnYE+sQY2
sZn2g1dMHHePHe7WNpCWvB/weY3mUhpwPnnIkafzTHMq3zM++zxeG2QcM+rt
21Q67zNwVoqYaYFb2WHfE3Wfc7fa+eT7Ma9L1zxJdQ8Zt7D5B/yUosDU57FD
vFDrXVby/nW/+7yq5HM8mt4fLzU5pMGe91dLscBRrOCkYSe82s68W6A2Z3yx
VuGd6mQJV8ID5ooC1hacdrJ+fFKVR9LR6+c7zO2v/U3ZX7oGmEca53WfPPbI
sb9AqaZZLmDGWQZz8/6fUijvRBbSmRIxQYM1u7l2WG3O5l9Cuit0bB4gn4P2
eAUvf0Knz8mu1dtdmteDmalzN67kTwpo0kZRYCW/v4ccGSXSdhzQP3LEu27w
jBSB3MAf7KVlzgkjDlWqWsgI1dnDhXnvd7JtY/OpR+SHj8xn5ORTPiZnezqX
/vk/78i+nPU/zzpz9Ne532GlItYPnMrnFzHuGZlz6SrzuS6lpE+kv7C6x/yY
A0xkK9lt0aCr5wpX9mQPnUR22PEHPJI6fNOshx3mPKzwtUXHPz2G2xPPIGtg
icwbIm531kAjndrgVdbQrOQDVsgi13iXU6cBB1gF4g3sXp9Zzhtd2UIIJSMa
xhb8y2nb2Pdf4NOQK8ErN7fY8+cs7N/2fbpH/o+Y/xU2xev7zgiZWM77G0sn
HL2mHsQsPVo275z2OQDO+J1D1pUifO5OZ9y0yNKXygQrSHWNHZjkfw25HCD7
Cj/ViPrWshwVpOV4kLN96YmJL1TK3N0mbGQjtugJX0PKB7zjjWIPakGyLjtk
COSCrcx5Lc42ddYQp5n4NDviv8nCJex72nuAqTlPxjsAn2P9ed3P7a713z1D
z/fpZSR/jgSaeYRi2eeiDSKO5Z3fHsc6C8TMufATZYUzRYA+r6cSOrA08rlb
+dWtrRVpbbErr2CR2bPPOk+FyHyHHs8b5IHX5hwfcsVZu10r3vbOu6XsUoP9
x8huhehiCxypQRaQ5kdsMT/moOzvAM1k5+EKuWrTRzKsGrE3iH6NNeha2R4x
ADIefPIjrwpnAXheRc8Zu37Sy8Ez7ucVeruY9H3Pn6MAeXfnSFYq3jUmUwUq
MOv3/8wc7x+pLjDT9efO9H75sAAlJEtbTMxtjb29Qq63lje4sjvkb7WmeFB6
LRAkogScOrnAT0mPxkY2BjN35+63ivnSOx41HYjzYI7yPCdowB2sP9lFLW4V
iihWiPzIH6I+kAnGfHNkRDkLRUNT8ymRPuHUJ8U5s+58P+d4r3Oux9k9sWcv
N/8hR3ZC9nlMmGuex6fTzBp4/ycZ3z4PbokIySdseW21lS92ljfrq5WqOBvt
tyt07dLPbzCtJ+3UR+3QO3yvYJk3RjbRxpx/00D+5G0s5YsrI3PcGeYrRPcr
WwstvIXuVZgjkbzOCTbgAN9w6r5qI2eEKHUr70ItXuCKsKJIBHJuwTSgF2Cs
5HNiGAP4NfboL6L7+NljvtiPgdZcZuURxqi35fkOdyZI4H6unXk9IKzAQna/
0s5n7T5qpqyWJ1kzVlxDvjtrtL8d39910riH5z3CL++7n/aI+l91P10jGnQe
EHl8Po9lDrvhncie8dfIRjm3wacDcb7YVfe6N+geZy958vycJbSBJrTd/ylj
OKqiWCiiJT+hNucEF8pr2RNAJhr72xwZbIWZu3edmVf1cu5FRATPO7Hy+PAy
0ve4wuO5sDkTO49NZ/0nol56Byh7WrzX3Xs65sqCvAJYmHf6VcLNyakjbpv2
0hUirL1xXlOKuVMsnua6vOj2Jye7bbH/D7jqa+zenfkkDyKAhfIyxudNr3eO
+9WQbQvvwhxvi5gixYD3qDad4H9u8AhtwVqIA2OXRr2EG+n4TJgWs4q5eY8z
44+5vhdAuyzD/sKyOrp67gs8sooowB97zg37PfIPT/O3Zj5EdSJw4LRibkXe
/V8o1vHZmDEXkZXRmSyyIzPEWNnRszHyQ1tE4ntY3S0m9qSJPm872Zy6fzv1
ePu0l0CKiAEelQE2isUb80ljxITZV0yUcat4n3ODT4gkd9KwNV7rBlHeBpZo
q8rUXvrLynVlPj2kkn74vDN2k5R9hag0zkmaW9T/c75fYK5RbbVeL3KJX7r+
89y6jPv7Ihb0e8aK68xmWT7Kv6c0Z7mz/9Nnn9IesL+mVmbGzq1G0fda+bvv
/qQR17D+adffYsffdfefgPq8Ek7bwmbvsB9LSKeS568VPzIWYKa/VGV4j0dP
eI0VPP8NbP0Kn+AKP6X7bqALd0B/1sAH1/ALK2WUE+FO3j9YKr9dCHlk7W9q
PhNsrNifvb/eAzjJrnnYed9vOSafV4ovyf/inp/20g40eGIx5zk+Y9guRwtY
NZop4/Wdz8i/FrYzVzZUCRvyiXqlEBLW6Lfytw0ytLTfD92/JP97+Ohr7Pjk
9x/02EkR/Ba/sQH+R06Xc8N8wkQlrG+lW1v49C0yufSbD0D+rhEJHjBNdCkL
tEbkeoBuVtAF8sFK7e7oDmH9l7owF9bp9p8z0jj92a/deY59vvvzKHxqkRtO
svsvowHPow7f7cxSIhLlZ533msFP6hO9fQKyd7g5L57y9vleFTJwyoNM+tLY
379Gla+FJb9B/n2HeGsPuadq4CMy8ydEg9fw1Td4hSN8ARE6MoUTB5Nz+zba
rYXe39nlrWIAzolbyePvkPel3f/Y/X+N2ytNlj8Jk/LTAyp4HbLNaiO3zCtA
3POMg2fm/Wtj81nJjpxHR31UYcfPNCC4txGrX64C6HlocEB9Lkn+nGCCTfvP
Mek/H/8S1rjmyIa8O4rM6EY4sDMonPVDS09PTrZdss2vYdNp7W+7XXndRX93
8AcvgQI8whIkbDjZ5QP8NHOGHfrCyfeL2VGtMIEWeUgrX91CmjX+UZ8OwJPo
Zx5ghQ6494hPdgMdOdhaNmUOVupCr9gI7XQ7wMqHR8XMd7jzp0JLPfoLy5qz
r897P/JILJhil1m5vQ/cP97HUYF5Fus7b939g3eATMxn/TPvWSkLnAmJ9Wis
UmRQ4CoWitO2sPon7Pxk4cnB4H5/hK1/1f3zjCw94wSL3CD786kc7MRh316h
CKDpY7UKElwjQ2iU66U44hr338DqpxmS98g2j7AKG3GDTog0lkItWtWDyTta
CnlshDh6vyetv9sAoiIj1QFz9Cfv6vAMP68A5Jhs2OPLyD/qOucYc7AC/1ZX
oMcCzhgZm5/0UigPnivyG5tPwyXSs0KtpFb0z2lNyQ8zSltjFzMLe+q+3mDX
3cMm33ZftPrX3S59gLe/slaYXmveCdiaz5laiktSKV5cKuck32cNzdiA27GF
1z/hK+EAJ8QUd8otUlZxjThzA0/kdb+VYg3vG3XOL3t+Fhadkc789Jzau/7y
CVB5ZS2vvua1wbxOf4nlehRexVnpwTf0qNBRgdDcqTlfgKcljfS3+uQf5sRT
c7Y0MZOZkb1VKJpqgQWma3mlK3wD5P+E7Oxlt/tvYPl30IkTYvMHaU2LVzgg
T3NWCXs8l3qXmXgb3tmxMvYerqE9lOZOGece+N8Omd8RWsYY9BbvdIQ2XAmj
du4od3spPMDR78p82ohPC41+P98z0fvl19mveNiDnB2YV2su5wHOp0x5nhmd
6fn819GZHuZcdT8VaaHc323fxLxfpxRGMgFmw3h/Ca/biOmxgwQa5GYJ9b3t
JH/q4oGUj+1hlR8gi5suIrhCJkjv3YgXUiF+YH8g9yN7N5j7kUlOndwrXmiA
9a2VcVD2O3iV9D5P3TuuoIkpDiwRpTyoRnky5/mU0qlG9YHavG/Q5z4Qk5qa
z8uZ9HHAONtBlumDYzy5LAKBufQanelVHoXOzfH+sEHTzE5NFMmwmj3rrYjP
QWDn19h4Xod3b3PGdqm8n/1YK6BxR9jcHbzvCbt+a287v3/EPcn6P6IG8IT9
2QoHOAjv88rODHiOZ3uJQTQT8ryGHdgIPSTzp0Tuv4L01sB3GOmlSaK3yAtX
eLcjdHCjyHKrV/dZL+xoavQ55qoLkP8x0Y5wu2/mdXQzR1PCwo4t98G5XJ4j
RpfUgPAskYW67Q/ddOsQPQKhlVNFOhOhPoX56Uc8WYE9G34qCz0D+fwbYaqs
9iRNuUWN56m7vg+d/f+sk/kDbMJBnKAD9uwTssONMvON9jS5ZbVqTawuln28
5nXfnZWSpSNIB0j5Cvt/Az0j7yf5hBWigq1qjjfIBvdADH2GxNpq5TVlH+/Q
zhfm/AhiPvmMr2D6eMQdlfe4+uEF8g6gS+E/5zzkqC7krPS4FUi0WzLvAfO+
Vp+Bt+gjwdI4+WmlGtoGlrmFzc6ZdTvE91fA2o7wwtfAf5MdfiF0/pV9gFXY
YTeyXltJa3bwzEQaWE328/8OqvETs1kq+pzj/mTN96g2JsT/Bl+38Di3sDtX
kvwaeOCpRxUZy86MM4FKYQ8b4/SAFGuOIf3CfDIe56BE14Tb9Nhbo0wuUXv7
rce/LP/3eW/JKLPpY4toNeeH5vbKp9nGiXYToLCF0P6loiLWzrwbgt3ba+GA
GzHydsjud6rI3XVf18jGnuCdr5Gp3cA27HvMmHj8HjJhL1+ZeeelkcFzhPR3
5r0hC3O+EDuM9qoHJgvwAthDqkfdwS4dhRbugRL5DPmdsWetMJ8ny1NefCow
u6O913umqzTrY75ctu4TGB+a5cy8iLaCCXapKkBg+OfZR16FMvn/qAd6XpLz
f0aqCNAWsM+Z/d3E/GtF4rT7lXgXa8T7zPdbZF0pA2e294jM/w63T8gC98Bn
GBfS3icLUii2OJjP3WB1fona8loYwBr7nO9MrgBjhLV53/gtpEzff4VY8Aoo
wx0swab77r0pO+WCXmXwkwojB4zOp0WG+BRGvnR+rkfYAZe2T1UMVD6fw+u6
can+r/HZ6553HcR8l/zU1zxDdBSINo1MCD/ztlYdnIiMc+4r5EnkhrDPYyfc
ZwNf24rfe4s9eI+rnyT+BMkcEQ1eQWeOthEvtDXOe9kr/uZpb+Res4+M/F+e
DMP630a4/9LY40Hmx53igMfu+cQaiAew+szzaK6lAewcKvv3K6Tpa9WFfQbu
3GJa5rSP4SPmn5tnf4G8xJmQERmc4z6Xwn+9upizv8LDz6QNrsMucbf+3PfO
BOYji77W75xfcuOW0gJKhLyOtXbgTjyOlOVR+vS7d1389woskBP8wBGPX6Me
y06AqucH0co0qsquzc+MapBT1qoU7YT6LRHpb5ANtsgkT4gK97A7L4E5XQF7
vhcqdAvMaQurcCs2wd54GkzT17E4w3oqJIj9TnEGtGdzcYVzfH3c77NYsRvz
St3oQvIPVDGfPZ/bds/p/HmOE0aFMOJHx4GZe3vtnfWhNartXnGp4L9vzOf8
n7AHb4H6EoFnjn+FGOwT7MQrcQLICudpr7fI23eI05fK952nRYx3YuRstsgh
K9VuePYT/c9S9eCjegBSzpHehcxystCvYDuoObRSXlOmDfCZ1Zxe4LlPKcyf
Zz5M5Ru9+p9P93RrGxPh8uwqLHR+9S+18ngu9vU48zn+3oEORYdo5ALJv5mx
5zHO9ytUFeUpquwNZvQ/N/Zl0NMehbRcIfd7wL57hPfddfJg3f8W2fgJ0cIJ
j9biaREF5Ol+K6F9nA/imaD3FvkZMLWwxxKf4gaW/gTrvhfa8IT/H5AL7IUB
JN29g/R3iCW2xplRnFEVXYOcRMIqB+cj+HScvNvP8TXrr3vImvlhZGf2G824
xHKdy3PAfDZFoNM+I27aM5gcDZ7IT1DHY/6DT/bmRJV03Xm6drB0S+TyzOJ3
8LD3YFs9dhJ/snfwyS/sDVDAJ9ndFBPcAxl+gKw415+x2AJ2ZQ5rXiG7I9vI
OQBHMQXWsvhb7Grivnfw+elVX0HD7mENnsQ8uMNnuwXmsIbn2gkFOsm3lcp0
Gvk/2r5phos4WyquLSUQ3IpzlDWmgucIYGTol1jhh8KyxNlvOfsk+hPj07vP
YqTgzFaifuwD98mezvXz/eGorE/wqiRTcu938MC34P1dwfI/AgW+gszpB9aw
GOwROEq6R1USydaN0yB4/vMO+7dUpz9R4BvldXuwDa46PUsxxatOzmu8c404
5Ap5B3lBe9uIOb6QXVsqLizMJw0xx/U51eT+eCxFfu05wyOmbkwsEEHLrnve
H35J258zfd3eOOssP5/E68BuCZzzG7E/0Q7OvVgo8ysQha1V7WeFlrjpWj7A
EfgrYDh7Zd2p6vOAas89ML9HZQHUgyvkhBugdNfYl9u+G4ixJTnmDSw0ER9W
CGpEH62YQo1qPVvs9BPk+xr3vOs04D12+6679Yidf4eI4IDcg+eJXCmvafvo
tjXOACTTba4dENNxxuanaJv5DJicbRlM8HEm+5B+3vt3GR2ILv/cs497LQ1b
5DYqplP6DEuPD/NzwP3kV5/+47Obkh2g703RHlFbxt9XQFZOivOf8P974UCf
dV97eOIU+z8hWrvHqV53+M0ddIw4YiP0fwN/zArcynziHPnG10J2r5Bl7pFV
3IJT9mgfIPdbvPcLe9v9Twbqy/7ZWyAFB2nAyjjByieLckKgn3DpV6HU1Zmd
SXtkgfwFyzc/5S1HiszCX18qAjxHe93m56cB+KnUwfuPKgG1xKdAeo7jc4B5
8ovP36Od9E5sMnZ5EtsOmfwWjP6Eve3hfxPu+xJx4AHSfoLsX2L/X6E6dGfs
EVipgnODDG6lyj+RRs7uTxb5ANyJmeIOqN8Noo5HdZW+ggV47CzAh+5fYhm9
EefkEbaIkj/ASpzUO5I4a3tlAZXezWcMsfeRJ4F510fUece6snksH4hbzg05
7w/P8fpLLPftvqt9nnPEBTkH0NFrtwDT7PdMv700zrr0SVuF/C/naFbGWU2V
onCf3vIACSdO1xNyb4/FmX0/QkIP2O2pFpB4IW9QJzyJn7sEdrgRR3OrvH8p
2SyQ5/P8v8bWYvsdjGfCPiC2PKHO9Mo+dtb/q+5dvrVPO0140elCsgPkgiUd
usW+3wpH2srLM5tkDlAIeSiVAXill/WfiLUDZc9R9YjFZv2OC/uc52OXkX+w
u32iQ9QZozLtVmnS60FwAke/sQGcAhrdsQvxYZewzYXqr2R9sNN2Bx04Iv5O
fV7J8l4DC34CCnSNfbjp7r2DHWZtoEXOzpM/UwzI2TCV0D2yTdeq1lRg+Rzg
uTeI+tewHk94p1Rlfomdnnz/F53sX3ef4b67/z1ykZuek8pohJVgsoZa6NzB
/DywvdBmP//C52LEtBxnz+W2PmLtieURdl51y+3EZeu/eRySPpPjfqPs8Zj/
5rmI41mRDcR5yGPzsx/XyPXj5F3GyESCjtixLxGNb4xTHfbg3j7CFqRsL2X/
L2EL7pABpntStkbbf2VbZfJkD5XCgRrF5Rt5ZM5/SNgQUZ5WGeQ1soonZZxv
gf6kW5/bl51FeN2925vu/xtYIPYdn6wRI3htPKWY54+SV8oJ1omBXCn6n6oS
EFLNp/7/Fn0NfD/ffyGryNMusc59u3+e6EIOxDJ+YjzL33ZcgPaAXd+cAe99
/w1y8rKPAFn95ZStHVDYBlLYo8p3C09wixjwQT/dIxJgTvCICJG5/xHRwBER
3Rb/dqr++IlwnBq0wD/O/NtCZ47Qnz2y+8dOzk+oNLy2T/D6ybt87H5KtuAF
4v83eMat6kPM//f47HP4Mbf/reoCPu2wQMxHjrzPfg/ev+fO4+zqOwoQJ2/k
nH9K5ZIcoFH25Twf/wyBUOb1qalswLSXfR4rkPlZm5+oVQkbZ7/3CtV/8nJO
iP1ukHtdg8l5gwjvgCjvBj+la/9enuC+k8cjeJiPiM9uoQ87+HDODdhJo/aI
OTmpaydfQ5tA1j5PBmFHyRU8+i1e+5tu/3/a3Ure5yW4Bu/hCT7pbr0EMvQE
VHCLiHUpy1PC7pDH4KiDz71c9rvH+76d/x9W9xxr8SvvGXbOtXN5necEv28F
qsj3pnUnZjU6eySy0jxWmWSfz7ucOOnNT79cKh4j0/tgnIrFvbrG1XwJv/og
Vt+NWF0PQIJvEPE9IuJ/Agr8iNzwBTKyA1iAbplZpWOXJ7v6fE5fazshdy3y
iVvE8VtY/ifF+emd30K3rjvr/wbW/zNEAMkD3KIn5EEZCLuUWvmaJSIbZ515
3MMIsDTHUSawme5DA8kLmT/ng7qliGdRAy55BpDHfvFTYJFR5clrksEAnupv
8tNtZ73tJ+fVJ3BzOpef/MPaCytxZNbcieGZEL+j0P4neNrki1NO/oAdmKK8
B+jEm+77a2RuG9Rnt7DKG0STtSJL9hZUQvr4js4v30GKrCLewMunfO8V4oA3
Xfz/stv3b7r3TLFg0rfPuk/2gBjklTSNHPKdbP2mryqs9J6l+dzjmTCgItsr
wawJpkXEdR4HBPYe1dZLZn/Wy3d8Zv/zE4fdn+folCNYjvx5FDhTDuBnAc2F
gVRCAsj1ZL/etVAAdnERyz0Z5y0R4XsQ6vsoG5Ck8wG338IfHFD928uCexVg
3fN5N+ZnOTeQ87Wx93MvpscOiPMnwJxv8OqUf8J/3nf3ftL9/LbzBq+hGY+I
P9+CBcIJMntoMOtIK9uorrgS+uA9KbwWjtl4vfc8848qf16N8TlLz89+ulz2
ZxYdCOc1oEIyDa6P2yXmL2S1RZXYwPcxfGeta2qF+alPrAASB96oLswe/1tp
AS3yUQz89+CCv0b1nX7+BfDfN6oCPsIXb2C1r4TtXgHfYV2JLNOVWCA14oyT
eEYr+JqT+nuvgTodoBOvgSi+RGTwZffTe/iAJPtvOy14D19xixhwg9xlY+wq
qWRx/LwqTrIkEsyzy/3k91EW2eVaEEzP6LCPbNCyn63Xl8ss9+85JuEa6hlq
aKd7LepBWCTqKSMGP/eFvVhT8zPVG7EzOHWLZzszZquB3ZHbdQ3L/gQf8IA4
/x74y8duN76AjF5i578WUnBS9Nf23BLyuw7m3R4b4ySJrRgID+KVv4D0Uybw
Bnr2hPzxCbs8addDt9c/AgNIUcDn3a0P3TNvkXm+QLbJ+iLtmk8bWEr+fj59
zIgdif/jXDrHUXLEP5f+c05mZH2XzPwpwZg94Z/Eo9HgqwYf1P1RZDNhC0bm
vcB+EvhKNZ/KfNoyz/JaqfK6VaV1C5TtDeSaIr0XyPreIQJ4DczvHrv4BbzA
G1jsHapy16jrkkeylR2m5S+FDZe2Un1phXe8Qv3xpIjjWlzDl0B8b6AfD9CB
R0yeeIIXeEKm+BI45LW8zcp4xtfe/GQTn2tdqeLgM/An5vMSZr0FzzH/HPmJ
n59zPfJHLrO8mpfjkpbJPqpOESdERBJ94I5vJo0qjfjfyDgvn9MyOWl5ITSY
vK01sPwF9vA95HGlHr8rRflX3R58iR35hHggzX7gz7d49o1xJk+K+m+twHey
ilvE+uzVOipeu0F0RkThBfzNAbXGt7Dr18gBXqG/5ADm2S3+f9HFgy/ga1hz
ugICcUJ8sRbSlKwPqx8+MZyRwNSKPvsnqpbzbfxKziz37OfReF7xHZ/duoz8
cwQgMpCYTOqPBA6cT3/IOSD+26x6VooTVsbuOE5nWmPvcLb7HrK7hhxfAGN5
7KLuK2RgD/DzKSv/0Fn+152EPkem9hKIzA18Nae33KMf4whZUOKV+P7sDD5B
IpzluIEFWRpnCpBz8oB6/x3iuz2Q4L26zO5geRIqnPzAF8gCXyEHWIuBuBOP
lbjWFFjQQbFOZX7+zxI5YHyFTY+rP+33Ue7pz3PE/EyGS/J/JrJKLu8cX8xP
qOLn88mOPs16YnFy7ESxP891m5uf80a+dWE72Wif8ngydvregXF/6q5uyrfe
weYm7CXF45938n/T/Z8q8o+QFHP1B/DCWdMnCr9STnkDhjH7NHwmDOc8HuEf
blFhTBEcuV0PiDbI9b2BbbmG5X/Cu9yBD5C8zRtYDiLPx+4TE8Hci8XCOgdn
AddiAS2E/C/hA/LKus/W8BjqnAng2GoeDeS53+WiANeumOgXEZ6Z5weUe5xV
HSix81Yc/WPfQ8zC53QcTuGnhI6wA1vI7hZSJ6J/g9zqoZP/C+y0t7C7H7rY
6wG3H7pd+DmisU+6nz/YGrIja2cPy96qEsP5bSfjxC6eJEHPf2W10LsGPueE
LrJXePUb7PkD8tIrVSMYfx7FRXzfZQV3QiuJ+FGPN8bzazjbgPg2Ox551kfV
29Pg0DAHmEvq3vER/V2BDfKemLtx2QwwIou8KznvSnfGavShR/1vkfkK6jYz
AHaAMBIkL4OzWTeqlLaw/YlTsccOY7T3CjL+CBv/GtWXhL5+Bw+QqnCvkQO8
Qxb+GrvzWhXhVDHcQgJrvcMW1cCDuGWV6n43xqmSJ3UQ7rGb2ed9DdleKxK4
hf6cFO3vEXU+Aad6EhOInCOeY8FewkpYECsdnAxHFug8s5Ux3T16P8Iz5N1W
edR/7qfzHfp713lOUfTe/vxdcp66V4K994Ma7J1OLv+56uLst9+bn9+9UiSW
qmcvxelIWNtdJ+fvINnXnQ1Ie/yzbv+/Bfr3B9zzBCw25eWfwA+zQ9sjvr3Q
vJWYJYz2K1X808+3xslyjAWvIcmEAbxWRWmPTOQBmd2teMkp/l8BC7rH1Mk7
ZAp78wkFjSwBMQcynCvlnaX4cLPeZ0acFVzraSb58Pt5zTe+cl9xqf6f8zjE
nsl50r9vYJCMXhe9noz7LJDRAk898QlpjawjsVnm4Adcw1W3q5JUT4iuWWn5
vJP6u07a7+2bThu+s6+7218Dn/3Cfug04VNU4h6N/YCn7vf5akdjp+5BlV7W
YqusxphODFyI9XMU6nODHb4V338HtImve7SVZkDcImIgKvAVsIKDuhUq9QQV
kjrZz7QCc/PzYWaK/mbmcV6OqvvVP+d1OhYQs17jOcEYuIQFiE9wHnt6jSHn
/LrueS3Cp9g7s8GxYu+IZ9/FQpIg7kvW9A5Z/xXi62TTv+x++r776ftO4l90
P30LxOXzTtqfwQu877zC191Pn3T3fQRTYy+8ljjhHiyxHXw7WT61+nw2YoY0
iD1rIA0pZkvsoXtUGE/4Ta85H9Trc41o8Rp44Q3iE6LD74RFs2rJGdKFGA1L
4zxqnwfJ8+hL1f/HwgDMwocHkyrqvd5tGRU2R9/yGPHS9Z88As0RnpEig/x9
gxFm2v3xXJ8Eys4nzv3waa9L2GrOdElX+hH7PkkzyfZVJ92fOsn/0u2yrzuJ
/2I/dz9/DzuQvMJH+7GTWooE7mGNb9WrfYRkr8W6OcrO8LymjaI/dh6lKiRP
ErkSgn8yzpC8Qx64U3/AHtH+DeLFA+L+J8QqT/BASWdbeP8Fns1zIFtJnSfB
cR7wQr0OM/Opn6Ne4jFVxc7k6Rw8s+B7uaX3E1jzSQGXkX8gPNHX6/s9agCu
t1NzjiCrvZ4lBqeBJ0Jy+ttSHTIl8J+0Q5+UvSVE9W0n7cS5+67b2e86WX+h
CPAnoK9/tn/u7vkzNOIjYr6P3e2P8BEJEWLXzoPwwz12OvElzuykzpFZSgyI
U0Z2sOveS3ivPt9HePxXeE32+u3BLTmAD3APLOgoK7FTxYd+3lng5P6kToSJ
+clA076aFlyJsKTjTAaOo+VMkBwNdi2Jvrzfv9wXRbwXMWmwvZ0VGqxAz/uc
qeC1DXq6Qt6Pkz9KsaJZez+Ay/UC1jx58+/x/8du539tf+zk+h2Yl591P/2I
+1IM+EunA1+Cm/Gy0xOPAt4CF74BHrARln8HWbfmpwOeEBvuxPvYAbXjXr+S
Bdkb5wlt1WHIiZOcBXlCzHgCzniHrOQJnusozuJS9V5GtoWYAJwRn3YA7Z/P
Q5r113bU24BJhgJYphEhG5O9HfVXPar0v3/9rcxi0uvBKNMPl/9EVd6RxRn2
494uTPWX+uQ/csA5eX8nDO6NKqzvYc2/6ST6U7fL057+x+72D120/1kn+z92
/76zv+9++qq79UOnIen+ZB8+ICpIqO0NEKEne1KHzkG7PUls1Uca7DG7lfXZ
IbYn//9eGPO9uJ/UgjsgkkdlB5w3kezGo9Bhepm1sj1Kn+cYlIp6OGd6oq7Q
hbj/c3nTQPH8+kZGONPtwIWC+fHb/OAy8h/1rxc1II/9pxba5v+C/c3PMO8t
/0wdbxP8/T51tQE2ewIH5wa1ndtOip8im/uyk27y8Z91sv6lu/VT9/2PiAL+
pbv3+y4G+BNYWcnuf9lZgy876d/BcnyB2y+Qkb0EdvsSGsBawZ1xkszOOCfs
aJzgewPPXYD/d1TO6BHgA1DlO8j8BTLBA37rBtWge+CEV6gObMU38KkylbRt
kbEdprgGPvllLGTM8RK3AdNeqrl0g/cR9aDzDuzZRaRvlp9AEByfWWZnohdk
YsEHnFheDfa65kTfU7/zUt1/pXnPbwNWx2tgae86Gb/v/v8EqN7HTsbf2F86
qf6T/drpwM+dbD/vJPyH7uevOw1Ikv9zZwU+7R75vLv3S+QHH7p7Ej7/pT2h
avwJIsoH5XQn6MMT2DpECdfy/9fQmD3qvXe2E/P0DtjiERb/BbKGNP3twThv
8B5xwEkadGt74UeV8TQAP9OQsw7W5ucAhEU0YSTeUTHJ9nb0huQWOZD+8ww9
Rwp+74ooj3Znps8x6yXsMalrQ8yi9ko2GWBE+6znuY7l9wvEw+zzuIIdfsJO
+qaT6atOdh87eX+DXf5jJ9m099PPX3W3fuqs/t91NiDJ/wf4gD90duEd4r9v
VBd6hfg8yfMT8Hj3wBPeIMNgD9kJNmGHaHEPXuGVIvs7ZXj34vQ/IOpjTfkG
1p4zZh+BFbALjGePsYLJyXG17FstvkucEcgz7xbm07/ybC5Q3PMMO+Ko3MM7
MpBrwSXl76/ndSav5JwzA8Lqj6QdRPvm5pzWhAoxXvHpX0R7C+TjB1zXe2TR
qaqarP93nZS/7GT8x+7f151U/9DJP9mCH/Bzwn4+72790NmBv3YW4CXihR9x
33fg576Gd3ivLo1kCRJ/lzMiH5EvvkHN6AUQ4r1YfzxVgCfLvYKV4HyPl6g+
3qjP4DWQ342wXnKGGFG0wJFLRRhLYIyFIv44C5rn/PLMK0fWJ5Lyc3z3XAfy
ebx5xpBrzmXzv7zb2CsAHn9Ef1jU+h2fGpn3NE77ZxTQA5/43qpS0uJKvhfK
/xU8wKedfL9GjP933c5Odv+bThN+7WT7p+77P3Sy+7mTdtKEv7P/BBvwPXAh
IgIpCvxL9zpvYBN+6WSdvh7wyBedDN8jX3yBvXynHqFrWIZtX8XnxIHE/3gL
u/SEOPAOEeS1nnGCJdgbu4c5CY5TJZgBOuPTe0z85OmluuCI/8x6Tp0zfyKX
c4v629z/nOvvueElV9QXXE+jC9StkJ/8E2wA11fafj6bp5rSB86ME+AX4Hzy
Kj2oov+EjP9reP4P3Z79Q6cH33c68A+d1L6DLvzQxf1/6W7/3GlB0oC/6/Ti
z93/CQP+qfudHxApftV9/xS+4NNO1qlCnDKEj0AI30Kmr2FnmCE+IL5nrzA7
hThF5gBsl1WfE5CJPeTLKWM7+AOeRMc5ARtF+TyroNTur4UBlcaJ063YTyN1
fk2UI0/MWVTBqAimNSV/buHzep/bhEsyAM97vyP2dM8Q3d6eG8zNT35yf+GR
o8+6myP6nYsF72dp36l6/7GTeUL2vgXCQ3ufcrxfO8n+Al/wdff/y+5fyvw/
7X7+pnv+19CZn7p7vu6k/D14Ad/gVT4HYkQM8Qt0b77HrYfuO2uHH4QUJqvO
qc8t9v8OGeA17mE1+ApdB5xC4TWkI/ADVi9OYpbuhPXPjDNsOe+iENdloqiX
TCBHUZ8jfbk/j6nvgbU7Hydn++ce4xIrrPz47HOFPhRZ9OGRv2N+UyNTeKwY
xyvVfvJrpX1BZPwO0Vqq8n+Dff4zKjy/dhL9ofv3LaLAhPz/3En1V+z6j93t
Hzr5/tzd/kP39aH7/mX3rF+62ylu+LH7nXewCt8in/gTUKKEDyS5J034TN08
98jiTqgUsHP8Sv5ghXj/EWjfCfHdCrbhTjwOnknXClNuEfOTYU4Gc/obr1Xh
mgMTWGjuQWMTxYBx2mvk8tHFwagq4oB5f8UnFnv9vO57qfpv/nqO+kx6LQyr
b73PD7THo1RHhxwB4smnfiJag6r8DoyMN6jyfQSf+g+Q8z/AtjP+/wUePt3+
Gojv19jlf+r+pX3/n7tH/wjNSDnit9j5X8BjfK864Z+7V/4Bv/cpaskp/nur
qP7BfM4XZ01sjT2gx+4TEs89QEfo0UvJfwOuf9P7dU6Z5wSpJSp+3vPHGVAL
8zNNOedoZEuxoGbmcxviyro3zyuBXiP0K/zcTvgOvVT8F7Vel7KzEtwuBBqc
e6io/cc8wHSb3M+5aiHkw66xsxJu+pW4fF8Axf8ATO/XTm5fd/d9B5n+AKv+
DbK/bzvZ/9RpxN8jCvgV+z5pzI/d76fc8Ifue7IYHxQ//KX73c/AHkjo8Qex
el4A7z3B9u/EFmIXyF79x7ew8deqI+/AIqI18Fm/676ToDQ/r+hgjbK/tXhf
furjWPhPk03CmJlPUIhY+9y3ukwD+8m9fORpvkMvsyjzfPZ8IA+OTeecIO8O
n5pz/oPHzt9iv9tU/X6leuM4Pes1cvSP8N9p3yabnmo8P3aSTT9/0d36Gf49
2f+/dv//sdvtf7B/7KSe9OT77nl/7CxB0pofut/4sZP55/iNd9CUz7pHU/yX
uMOsKL5EnedkPiWO+H6p7u21Mnme8eM9PTzvqVZ2x45Fnky7NU77Y32ZZ1nz
vPe14oBpz2+fAwmembOrHS3xHCuf+xb7L6qq/qxzi//cCvx++QcrJSJ/7zoK
/p+/u093zSPDSR/7O1NwoqxnKZS8NU5pfMKe/wox/zeI+JLl/q67/U+dZ0gy
/hVW/kfY9n/Erk4S/ytygX/qcsAfkSX+0u37r7D3f4LW/NR5kc+613yDDPBF
9+z34PO9QFR37Ke3HMH/YzX4GtJmffigOg7nwRXQhb14vVvoMKs8jfnckgpx
QymLzzNoCjEeG/R+8WQwTkOIvDmQveiuyut9Odt/fPbouce/1P6PeZMeuwVH
2SXvu991c26BBHgcyPNfvAN0ropYaXP13D8AfXuFyl1C8f9o/wI5Jn+d7Pxf
4dm/w/79I/z9V8jpf0HdP+HAyQv8sbMBf+1u/dD5iz8jM0yyT/f/AK//EdpF
fPEFcj72chykgQcxxMkUX5uf8LODTA+q43JCNTW3hsfnDCOfX8zTy2gR2Pm5
VDWYkx9Y/y/F/vGTnpwB6LsrzgHOLf55j+9ztM915HL4T96JMsr28LiP++N+
tw+hDaEv3t9CDvBU/U88LW2DK53w169Qv/sWGV3a5X/qZPkzEP9k99Ot/wkZ
4Z+6/fy+e+wfu9sp1kuy/+fu8T9D/l90Vj/VhT7CSvwCuX8JJhG5QeTovYC8
XwivSV6+gjVvwQLbGs+A5xRXxqecIdX2LLJlzyO7UqcPO/t9nkny+Rvt+Na8
35snXJP96dY/n/UWXv5cttPe/ns+do7Msnc87x64zIrcPuTreG6OB3j112tG
4+x5fMR7Qqe9R5ghBvJ5S9edjH7AbJ3vgeL8gmz+fwa2l3bz32M3/333E+P7
v3YeIWV5P8tT/AHx4D8AK/gFOODPwIfTpJYX6NX8gM7hV/akmQG3xrMhT8Y5
kGSGXiEXWcEC7DQzgidRXIn51WL/80yKjVg+ftrLFrv+aOz5XEAfyPWfAA9w
5IfTxz2OyvO7nA1yPuXXq3HP6wSRjYfUL7X/8xgzqn1xGmWc6+P6MVWfl3MA
rb+fMWJt7IQiE/4kC/sIjPVz/Pu5k+8/dTL/F8R0Kar7C2q+Keb/T8gAE9r3
993XnzsbkLgAn+OZPyPzT7jfe+B+75BPvOseeYE+/QdUg3bo0XtSbO9cjS2k
zLOGGsUj6VSI0jiH7B5ZwEZoVZwnxZ7uheo8nCTLkydq6AJ7fRfqb6zNz4Hg
yRBzoQGRO3O/sOMrMmvf4WOL3C8/5SHP0h0XvoQGuOaNnr2/yd74qUX8jDP5
goUFPzC4IM4DYCxYGU9DXmoXPYDv9Q613s+R7SXb/Wsn+T8D3Uu4//edxD9H
TPglakA/dZrwBfb+V4j8voQupMrBj8gZH7vnvEaN5z1yi7eYC3OPSPPejuKD
U16cMLU2Tu1gPxhzOMb/7B1da4YA+Vw7YD+VOEFLyZRnvx/FZuRpk5xovIHe
EwnkFLi5qjnO8g++t/tWaoHXA8wCJ8wzxbwn5HLsD648q8+56OFtxv1nDE8x
t7xW5VbAZ0BMjSe98sTdhKM8gjv9LTKAH4HZfQe2R2L3f439/gvy+4+IDr/G
Pv8aEWHKAb4BLvwFOMEfYEPewOJzNsgj+sHTpKCUx3+CCND5G5zUy7Nm7pDZ
HW0nrucBMvUsj3Mg2u731sAEtponkLz+3NaKAErFC7V6PPhvhx4HngXDvT8X
63cKvxjoriNoUUkxi3jgeR4QiHBunc89we9ZPk921COUrhHuqxybcFZIoD7O
FfT5zxG5lIiBVmLG0JqmTopPgM9/7GTNit2X8PrfA8f7tbv1JTz/Hzqpv0E1
+AE4z+dAiNIknu8RPbyHzf8cyG6qJpG182A8u/UWFcadcvo746ntJTw6J80e
gNRWkPfO/FQCzvVfda/XQO5E8jjViyzWCtHeRvdXwoOW4vsUYv1PEf9z4iEr
AiNZgcirXOLRORke/nm35zk+NM4kdIl1zjXIZeve379Hjd8rlZ75xRdP/+HE
G/LeOYmb81pvgfwlSX8Fvu+v4HN8QEXnGzEAUq73ttOKz9Dzmbp/v4K/TzWd
L8AZS51BX2Iax2eo1j+guneHnqBHcEGcz8VdSixnjYj+iM9T972CPPWnhEbQ
JuyE+23gx9fyHBvI33vJONOaMw1aa6Uv7Pvh3LOV8n4/DW1qweTzOTmB+OR9
ga4Pz+twgRDYRTVglGld4Po57893tXf4uBcz/ey5LP+umXEG4BKVsVKcP56d
eAd5fo8qTpJ8QnP+cyflVPlJfK9fwAf4FRWcTzGH9R06bl52t9Msll8wBeQG
0xhOyCYe8brX4O+m3q23qPYekAOyl+cK0uO8lrXxDDeeAXQNy78BitOg8rdB
ld87yI7GeXKVcUrtVl2dtSJ7nvvXIvevFA+2QoHT1JcxfEswo2eWc+xz/MSv
XtTcpxYW4Lc2+JL8n5yNPM1eO89BI0pxfl+cA++a6ZVfvpKfeblU7xdn77wB
5v8lkJrkz9+jBvQT8rfPkfGlyO4VnvUWz3yLfU2W1/foFvuk268fkO3dYWLA
lWZF7BDp85zuA7KNDaJ9Zm0r48kv15rZcBSSy/NAk+U+If87qpNgp0pvq/i1
EZ9jIaTf55hwnlEhq+JnnXj3cyEfMLboAfDdHTU/30mR54VczM4rhKNncruU
9N2yRGzh59A50zM/5zsy2JhsPLZCloJ5/1x8eGZbrKvfoqv3LXif7xHNk/mZ
Kvhfodszddl+A9z+HrPXHjCT5Q32/QdZ+IfuCn+GOP8boEonTIp4iQoDz2sm
Q/dGfO9b47wBYvtr5PIb4b0rWfUNvnhu+FFzXXdiejhKlP6SQrt9pW7PuTDC
hXxFob+Z007ZBTPv90WwpBwPyq+4x3n5GTtmubV3iV/2/Bc7e2czz1F99o9n
ndMsP2SMvzDHMufmnd/8+8iGYO93i9hrjxl6b8H3/DOQmo/w+9+L4fcK/SCv
MeUvRXSfdnJ+g9zuNWZxps4bnv/DyaAvbIcJkC/B193L418D771CnM/Tem6M
pzwfYfs5JbzpO4O8U48sxVtxxFaYAOBzvWnxZ8bpTqzxMj90xHcrjvtSFc9V
jwTOlRfTJ+a1vqigBA/YJOk89j+X88guJffn7zY604S53t99Vs5Liyqkn2oz
s+A05V0hU1lFzsu9A9vrM9T4Puvy+j9BF75STsD/36AP4zV2Ome7pTNA3qF2
+AaM3AdI+VFM0mtVdq+wfzkP4B6ef4tKz0Ho3kbTeugJjpjhx1kUSW4nRQaV
5hNwfv81dKYSBrzS91JeLe34gypEhTAEn/lH7J8n4Tie5+f/ecdPVAIjGggJ
51yP51jw5XI/yjNqyR7Fm+x56IPLfixN9t/0KcCOYcz7iJAzQEtEyjzb+wEM
y1SX/xwdfanymzCeLxHjpd6uNGHjTnMeyeN8iRrOHSR8DZ24kexP4O2/xmOJ
tZ9emyd47FHx41kN7M7nqQ9r/M5ePcJ7RXMpLuHJ8Dx7pDXOj92BE3ZCDMip
5WR+xmnva/iGJazLHLakVV7ImeeFeiAn/f6J096jFhxdt763z2O70AOPwsI6
XGJ5bSf8zPN8P3jH3uU/zTwFI4DoAOLZD3Pxv1hFYcdc6thLnv9rsP3edznA
V5i0ytMcXmC6z2tgOe90xoNP5f+AOOARyM4L9HjcwjIc0fv5aAcxfB5Rs+VJ
vpzumfb1PfRgryrQxngC1NF4hscG8r4yTopogQBxltyurxUT7V0DEeZU+YU6
uzjT3s8S3Krn1GcfztX5b9hNwf7JI2WXqOOCec7FZwRHKzh6l4v+R2eyd3+e
dyidx4jnbIWRfAT1hprEClBpY3V+MMo6QKafdLv9FeK+r8DtJzvzU/Ru3KgD
4zN09LyEd08ac9LZ30/Yk/fQhhV6yHkuDOcx3GFfM8940Xsdnu3s58QyyjvB
I/DU2Svj7Dj2jN8j5qcGUd6cW3Ujb78XM9A7/HiGFGtcG+Oki1KMP5/7sjCv
/jlC5niK9dczJkJ4j1VgfmZ5rfDS1R8u19Hcs4QHcgs1yz7xyM57/mMS3EzR
f3p+iaiZnb9XOEkldel8C05mYnZ8i47v1AV6BEbAnc5zYNi9wzPYNsbzt5jz
88SGF2Jq32Ev32l6/L1yfZ4UcdB8seQRKlX5d9KTDWw8Z0GywrcXq2sHVHgr
lvgKr8xMkfWCEhXEpWrBZPpXQBI2qAVNxX5vLDgRbuG9qkPWbOB5I+0fxwTD
Cofcfb+dV4F+7zq3J4w3IleN6V7uezwbnEgn/CyAyHFnqoEs1P9RGufsPkKy
H4HxfAQH7ANywXvgOO8U8b1GvHeF6T87TAi5B4/nDp2Xe+P8pq128F5zuzg1
/l5efA/vsIVl3yHe2yLzP2nX12LwrqEDbgnY1ce5XwfkhZxOvRJrgL3rB2R6
e+h2oQ63BXgA5BXM5R3W8BBz81Nf81nZ0/7Kur/Nsb7I/ByZDVkFIzSe/fvW
c95/dP76pNK8FhnnvUz6XM+xAfdtftYhJz+3uDbXitO+QzfWT6jepk6QL4Hl
vYOtvwdjPyH3H6AFp05TeCrbCfjeE5icV5DvG3XwnYynMT+B6XECNnCAx+ec
mbX5/GfW81JcwDiNUSlnB5EPUEMT1kArOKOqFRvopFyB/IEdHuPpD6ue6bVW
fkF0kHMfa6G/jtmNhY24d4+9HCzrYOCFL4gzGvIqwWU8gM//zr2OZf8HC8zt
VzCBo3LgNS1iAEtYPj/xidNXTpDKFXq2PkMNj7W7J/Rzv0Tc/gCk5wSm2BFy
THOe9sjFXoCrxVn/7M7Ya2fX6NC81+yuI3bhTlWfLWw1M3zm7QfEfZwFsVbP
T3rnBn2g7Op5UATILOKx+xtu4e1PmjG+7jlifs7o3HimZfL2nHrjJ//5XmGU
HNLOebbOogzk9VzGuabEvr10BTgqTeeRX/BRvcMnz2QmZ16B+59Tb5PvWwgP
4TkbnLLwqEkvrzoNuFf95r16sO6Qv9/Ldz+qB+sBj62NZ30/Gk9iu8dv3sES
sK+YjP2j5sBttYs3PcpH/OYITuJWSDDR4INivJNt1BtGpie5YwdEAVd49h54
Emc7s0+gUd2n6iuBrSK/qfk5CPkMxXz/RD9dID1Rb/Ho7zwGCJlcZgU7wSz3
OW6BwibE2QQ5YujZzKiPcakBfvZB8rHXiMvJz/gEe/4DqgCPmAXzChjeNRhi
15DjlSq5O+XzZGRzNh9Pa7zCK94D6T/Bc9/Yybxvh3NAWvMTGlpJeoO8oAQG
fMSrbIT9NOoAPqn/h9MjWrEBOTXmqmeKH2A/0hTxvS1UB4rzjBdChP0E8NIc
Rcmvpe//59Ocws57HS5Qt7w6f6n837+T8+O+yKd6eF9A+P+pRediTHwc9VGO
n3ft8294xlOKjlPe/ilyvHeoALzEDuf5bk/w8Nea6n2NPt0rVHfYs3WHDOFW
eQCn9Xns9wj/fw+UYQ88j9H9RnjfQlpQIyqYQrZb8Pwa9XhxFjH3OSfIkR28
FyfgWswgTobzsz/XwoOZLRSqJS3Af1uIDRmVvpnl7I+8+/Oc23Fekx31OhOn
s1w698stft4NMDqTdfoEfsZH9P8F7uPRX2mcAlwYz/ngSW8nVGhOqNy9BRb8
GvMer2EBOGf5BaT7AjjQDlpwpz1HBOdKPTtJAq/wyD12uU914nm8W/iKVvbY
+7W8ZkNGP6OH1nh+3xHPvpJepPOnb2GtOC+gxjunybEP+M55oyfgSDVy20ZI
V2k8ZZZdwN4B4aiPV0kDXfM5IN5f7TY3PP057yuwmMvpwMx8f8fcMZdwIEH5
JEDPBZ374QxBx7A8KigR9/C8jwpoOs/QeUSX1lu7UiTGs/xuYAHuEec9Iio7
GmeDM9e7Bs7HSP0IJhdndD5CrpT6Uaz+DfLxVhU8n9Gbqrsz2P0FpN5CA8jv
5ZQHnvzgPWI3kj+rB9c9Q2At1HiNXc9Jsw1wIGraQtMfKuOpj4wD8ig/UBW/
4i732H3PmV7naMDl6kD+/jHpJbLPaa99jgB495r/NDXHg8fyAbT/ZMFx7vfG
dsLNUp72CpLniR5vMJUhcbTq7n4yOW4l3QfV6vdicLPOvzaeGEEWH08NerCj
GJsV4kKe9OXsLZ7DsYJ93qrq26pjh5PhT/ju2naEpaF/YWTJ82XvYY0OigWu
9U478Ah49l8pFnDS93Q9alVJZ6qUTvrr6bWfqK3GZLfYgXnG5TH4+fyFS6xR
9vp5/hFnAXsPesQsrjkRG+R1Ak68IUt4iupYoUjrCtgsz9fj1A1iaumLpzkz
CuSUjgfF3Bv8Vpz3se/7NPdga24Uu+3g3/di99AqkH1YYs/yDHI/JYA+mxNB
K+OMF2JHS8QqW2GDW039SfaJpwfcwG6Q+7Eydv+R5d2q65dVYc6+mOIqRD7n
vK9JFg9Eju/cX0deoscuvIBZxIOXkH/EHSFhr1tFFSAwi+ju4KPe4+J5QJz/
Nuu7oitY9FfK8tiX/Q4Tu3jiy5W4dzeQ9T0q+Dyll/LmbZ/YtjeeHcw63h3s
xw26fK8l8y3qMKWqNEthtD6dozWe0UlWVykbfoA+sma8NXaGki/i/YMneKhb
4A0pAmC319R4wom/Wwk+QJVVgLyfP6Lo8N/n/jxqPjn7Lt+rz3GA3y//iDXO
+WY52uO6Mes/Vcwo8vO+yf1xCzWTHrBSvgIDeI2ZjZy1+xIo/iOyOvbmHfF1
Bz3Zahb/Wr27zMuvjee17iGlGrk/6/neg30Qs28lf0/sj2dytlaLzXMw9u2e
hAmy+5v1XeLGPJW0gfY9iGF4LT28QV1obRuhAMlfzIzT/xfgCLVCgMiBjbyZ
V9DPfOA1d7sQGWI+ESawYD47ov9LRYCRiTjen8ccke27/ZnbWHvfrX3UBYj8
Ts0nnlZCgLc915pnur02nqV1wBT/rR57Mp6sxfx6L7R+Bzt+DYt8Db3g5A2y
uDfZs5ivE8/xM8B4AsdCPA56eE7rKY2dIHvsXj52j99ktapVteEoHiEt/wF2
gid/VvAi9Co1NL2U1BfAvrzzf6Gr5bVcxlD56TmuCedW3vUhIq5AiOL/37vc
d+caF17fc0PP6T3X87wh5le6L/MqNnEvTsKaqwa4RlX/Fvy8EyKqvfkM9Rvj
BI6TfPgt7rsGqrvSFL+dMN9r6MQSsf6dcdLEHj9vsGvr3v+vxD9gDpL0jP15
reRfgd3BeHEvv3/qEQB6Esb9rdCIO9UUd8KKW3iABSJdnvbOibc899E7QAuL
Ca/O+Blney3v8Tj/KeaumAXyE/Hi711uY3IM8HkNILjrwWJ0DNhrBB4JjMT+
L9QRWZifwtBgT9GDXiO/PmHXHm2nSgynbt0azwRcqXbL01ZXiMF4XjCrcRvs
wVa83Upeu+oZW634OAtV/Iqew0dG704/sTtpJU/ETOAE3eTMKp4cyhmiJ7EA
iP/U0IIldjl7fqfq/50o9uPkj4j8J88kHPY+v8rBtM/zPesllEfhv38Fujc6
04Ace4g5ZY4ROpIRO9/7FpkBpt8txIRpsfe2Om3jgCj+ATnVPWTKmusROTzR
X05W5byGRkh+LSvPrq1a+zfpwK12O0+AZN/upkd9eD7bXBFCK4YGuX21cYZn
C19Plkfa27fwAVdClHb9zj8hCr0xzv8jt7zC39gYz72eGCde8fwPXgvvnfM5
K77zorJ6jvGPMr8Qdj7yc7ug/D1ay3/OY/7Qinn2/i7v4I65L4tqQIF4oEJM
1MoCpL31BPv/JCyfcRYjqx1yvRvtuSsxNZ4gK+ZmByA9tdgZe3F7WX0/AGtI
2dcO8eBU+79WVO6T2b2XqxI7medFMQvYAqluNSm2NU6FuIKl2iOCpQ5s8FNp
nP3ICnCuCynGIP+NUZFHSTm26mygfMJ+zvk6l3jcE57hEiuPLUZn93htz7v+
zuv/Hi34uXF+wjW1uZANrLEnWmDjrLNcC329FUf7pPrbDhb+FjnZPeztqp/O
H11ZZOQcVNnfKvvnKcJ3Rr5Xqeh/rXy/UFxeG2fQ80zmGSITsvY4o6IQ5nhA
nMfof6OYY4/Y9BNoby1bs8Zv8cwHP/G5EhJcCPXzs1DOT/nK93Yef0UneJ4B
hiYE9/NyK2IOj++DmRa8kMCerP8bohbk0a1PDU8ZDs8+K1QNm8H3M4Y62VHz
ORhbNcq5iPHd2zvhqpwXzNh+p59W5qe6E69pjKfI7m0tpnHbPzZXxt9gb3JK
p/dxsCqxhLbtJMeNGAM7nOzIs+NO0CdOjH40ngW0AS60Ns6T4lnvy77SV4sh
vhQP0OfhT8zPyzZz259z6p09k6MBUeeLWlBg9JfSg+foct4T4pKPaC+4Kd6z
7r7AZ516X2glFqSf/l4bz145Gc/XPdmVvP5e7MoW2dYtqkErxHoH4ylLe8QD
LfC4vVViXlfi4LXY12TkLGWLF2Lh5FN7+Hs13okzAWrjdOIDdIp4JFGGG9ig
vbLARr7oJP5I0sfSeJ7RCjauMp5uuEQMWJrPQp1bHhs5r9aeyT1sb+Te7n/z
c3emvcQuh/86r8ytTt6LEFmn4xfk9o/NT4D1zzrXs9jpPBfuyanHnIt8EP+K
56/dwRI0xml7tWqtK3l/xmYnaQHxffZksyN3D6lxvhA7zHjCL3t6OdNtoUyw
NE7oWkJiG3n/xvzM+EZ1PHIBa8QiG3iiLZ5VSQ+2yv2ZoRI7ZJWBJ39T8jzv
hdPAmPnlExbdf8Zudoalx9fnfMCQdVjiyyKAOZ8rZxf4jqdGRLYSFj/vFAst
Gpmf/UQm4BKeYKG62Ak77qFneDkf62jsvrixp56Xf6UM/oBn1sY+/UaR5EZ7
mla9kJ33nG+tzi7W7Cf4TZ4Iv8ezW+NsmpVyuZV8xkryJ967Bw7kuccGNqAW
94N1Bp4CUPc+bobPxPO+ZkKAJxYTkyMGcDtPW3vO8M5x3nG/Jyf9811Kl1rn
Wd7YgtntviCPBnIMYGpEeqJmFIyhOfbDRGywFogOr90OPpaV1RY8jFugq/eQ
1xpsoFZR11acfPqGLXIBP0t+LYymUQRQKwIg12+JTCBJZqL7yj4bXCIjnOEe
Tnm6Ns563ULjmHvwn58juNHzWAUiF3QPHGqLv49cT0595wzcQjFRZP5hy/P6
mfO+fd8FDude1q2G94JN7XL5f1ieiPycdeTPiPpPsJUmZ/FKIQ9l8lIL8z7A
hTAZ4rCJf3svHHUnzgXrto0ivRvjBE76/R3YOzWe3eiV1sZZzFurxLlq1IM9
E87Ps4Dpkzmhb67e3aQVV8aJ1AvVATm7b2c8IZqVX86FXwudqPD+N9BcYgxl
j2mysrg0nw/D6jcRwakF+zP4EsH0mJtP/jjn33q+5drj9j7v1rsk/v+clTDq
9SDsUZ6B/DZHNQssaGbO/xrJzjbmXfSclXGFr0aV3Fr1npWu+854OvetIvIK
ejHVrnTsrTBO33cEzucwMarjfEbuXnZsM/ZbQTNZHSQCWMr3t+IPblR1og3i
KXAbIcJz2Zy90IKTfp4rF6nABOYZQEWvAXNFTWHTHTWPjMrseZ/Vee6XRwPj
7PZldCBqPs5IiorEeX+qRwCeC8x6qbuPWsjfLVQFTr/Bzmg/JesOcQBPYliJ
q8NdSwt/EArL+S21cgPO3V8qBuSkNdbxdvAbzPMK5eOFNGEJdIg7fCEtWChy
4PxGIn4b44n0dX8K4BoINTUizgtozU8WLoQONcYuEZc4z7zzWmjR73vrM8BZ
Jvlc7l5xC6mMnkk/xwouKf1Afvke+Xk1eR3ALb4z/2KyseOBoRul6h4r4znI
RHJZ7fGzoK5g41uwMJwlxI7crWo4RA03itNnVotpszX2a5aK65b6v1LuQGSe
9T/6hVIV2bWixnWfF7awADfGmeCbvvJc4xyhVlFIrb9gLX1b4ZGlkGpOu3Xd
q2ypK+B9/177m9rfmqbq135uubU934W+IgK7xHJOB1feAxCTKXPEL3zRzCJe
GavPxeMEzj6qxYwphAEcevRuB/S0le3n7jzAB5+s0ZXdKO4+AQvc2lrV+6WR
u7lVBrdTvt/C0jfG+UxEdMi+4xQ69uRMrZFPYh7I925VTb6XT7oTyrvGZ0iy
vlOEUEFnmSkQN94b58KszSc+cfrRGBlhIR51VNHHvR+d9bsrj7g98rP++uao
b64bl1i5Vwl7n1eDgoMWNQx/95hq65pg0gNeiRSNTcSD914g51VdKYpf4vqu
oRkb2QDOi10hAluqPsTuqrm8BtHkhdgjjLjI9doIBeQ5DsTnW/PTCIjMVcoa
idfvEd8xN31URfJG+UeFxxr1mCx7HgHRXmoQ8z7/G5n/z8V/LeQDKU+3npHh
5XyO2NXn9597+9w/XGZ5PO+zPPI8ZNR/6rAN4RNyhMr3vucFzogqVA9eKWZe
g69Tgl+9kOduZYO34nFsUQOgfyWb74h4jfk964Gc6Vhp1y91m2zclbWKBObG
KY1TWeYp9iZnNK7gT9jtQaYp+f8H83PiPffjtIiNldJR1hgdgdxaJQtDzgsn
QMxVD6QvDO9+Ps/D7WvsxZzpEeh7PH4ec//eFfFm5IHx6uPs8z2fUeBVYEco
PAbwqSAzZdjBw+O1Yr31gOiLMxbcpx+UgVd958dCVRZ6BEZvG1V26MEPxnms
juWQFbJS51Hd8/5WNhcXZ9bnaTNZFNYnr3pW6Rb6xioTY81GlYG18CLqIZkN
W8QaZACOVQlO+MPIeArI2MgBzln+5/vLuz7zWS/xWOzzqAtfMvYnVpPjPH5/
Pt09Z6dP+1vBYR1luuL4kJ//y73nszJ5OjuxuNbIvaRXOBoZ2UdUBg7amQt5
jFIR3hK2ml14694Cp/c6Ct1dCw2sVZdL0pjgtwvFflPcnoATTo442WmMGzkd
mvnEzrzrd4eMxGcJ0nfVYhIkD7CFxWmFLfE0WJMHGIkT4dhNyM/z+ZBynkvn
ecJ5LnC5+n+eccTu984exwUiKgydHWWSD60e9cj/WBEwuwGXyssbRWu7vua/
l1ZwqnKrK73F/lv2uZ3X7WrhPozj18JiFqr/0duzt4dMTOdmpRhhi2fNVbVx
NGljW2UgJzH/3MfURn5RKb1gzkD22EZVB54Aw86ihfn8D1afyIKbm08B5fIq
b44Bu4x/O98nz/ZDFy5lA8LO5Kc4hUa4L4j6Q2DFOV845O+TITgFbqHayAzy
4IxkZsrkbKxwi2frVJLblWpuzLsLaMjCOMHRz1zlGaxr43yBpepAtNjOOvHz
O2rVaQtpg/NBZkIHWlspp1gBh07vdjLyQNmD4hMDeBIU68V+OkAtS0PMdwnd
SpEgOfJLzYAIlDzH9oM9RQk85wflGEDYiecR4e9Z0deRxye5n3o+bdDrkO43
AjGYIH+lXhD1j3nYROrXVkqeS2MH5cn8bB1mgszxro0TulrVDDY4veMAabHj
biUkkHXfGrrCHIxVgIVwX2b4ztD03mwiRQdViNkhdKXI7oT3Y/fXEkiEn/nc
qhJZKR4hm8RR5VaVzlYehj0hC/O5T7O+XjqW54w5ylHtPUd68qj/vPI/yjTl
9614p9zL5Kzzmf7lZ1a4T5j0UYB7fX+Us2FK7c1S3RCs1nDPN9CCg6K0taov
1ImdcB/2/+3FH+X+3Sov55nrzujwea7OEa2xswvl+0Wfi9XSwUKViYm18kDM
UMkuX8vSlECqSunYyjj7p4KfYVTZ6pM1uIdTnyaqN0wUE+bzMZwBHHm39Vf2
t9FfoP3PZXSplWf/ucWJiQRRkeD3iAUnZ78V2jyTNSTLipNwS+yOWruQWf4K
1ZYlZLqFzZ8LXYteTo+2/DQe+okdrvmdkYtFRLEVRrdS3ler5r+W/JbmU1pb
RRQF5NYgljgK1V+pmrgS05e88sbIKyI3oTJ2EnAKMOMKeqeFEACef5yy6QUi
Ip+QYeaMmjzHy/PpPLo7l0Hu/S+5flvHGfXonmX6SgwoJv/7pPCoDMd0qIki
n6m8f5Icp4L4tWcNjuyKUnuSNXyes77Fs07KrlfK4xnhEQ9uJb9aukUm6E4o
TMzsJP7ASlFhnNNaI1/giW7c1zsjl+Ag5K+ybY/0cO/v9G4NnsvYj77Iq5xT
6FhpM9V+aHfiRNVzfr1f63M0IFhVLpvcMlzq3Je/rQV5tBkTocyC9ffcN437
z+xIYPQCEIFhVZxXiL5ziV3e6uqRgekMH36xsnMw1nYaYXs+eXmvHK1VHtBC
E1gR2Eg2C1iDmTLGqZGPR97H0qr+EdbwN3qlDeKNa/MO4p0yVdr4ShnMSnjx
XhjiTnhyAYRopirAHNa/sOnZ1Zkodoqd9DzuD/5/noufe4v/KOm73rkHmljw
093+P7dJzhOa9b9H78dcmzw8noeRsnCekrkShyI9ypmrW+hFYZXi8VqRX6q5
z6EjyYrscN09FueUTtcpxnyF5M9of47fXUMDG1gJ5uyUqOPBreIS6scR70Dv
1Rr5q/Que71aqSyQ7C/2gfvJT6Wsj+O/nIQQrHjnULk0J/0Vj4zQehmY+e7P
vf6lIr+/rQfO9juvQuXVymCi5tZp3Fs56jktAO+ZqzvC40Ay5ljN2dpCvnKu
7Jl5+1x2fWE+d5m/yTzbO0vnyjFmNtXeY6faQu84tnnvj5mHL6GbpeJz2oK5
fNHCfHJ/IVyRKO7IyPPjs4go+l/DGgIzjLFYz6z/cg6eo//n1bzR2ZUN7z7O
pBCc/JDOsIY1rGENa1jDGtawhjWsYQ1rWMMa1rCGNaxhDWtYwxrWsIY1rGEN
a1jDGtawhjWsYQ1rWMMa1rCGNaxhDWtYwxrWsIY1rGENa1jDGtawhjWsYQ1r
WMMa1rCGNaxhDWtYwxrWsIY1rGENa1jDGtawhjWsYQ1rWMMa1rCGNaxhDet/
xPr/AfqKMLE=
"], {{0, 256}, {256, 0}}, {0, 65535},
ColorFunction->GrayLevel],
BoxForm`ImageTag[
"Bit16", ColorSpace -> "Grayscale", Interleaving -> None],
Selectable->False],
DefaultBaseStyle->"ImageGraphics",
ImageSize->Automatic,
ImageSizeRaw->{256, 256},
PlotRange->{{0, 256}, {0, 256}}]\)*1000; igs = ImageAdjust[img]
|

✕
dk = ColorNegate[Graphics@Disk[]];
p10 = {155, 120}; p11 = {160, 138};
p20 = {123, 160}; p21 = {133,
180}; \
\
Dynamic[
trm1rct =
ImageTrim[igs, {p10 - Norm[p10 - p11], p10 + Norm[p10 - p11]}];
(* extract circular region around heart: trm1*)
trm1 = ImageMultiply[trm1rct,
ImageResize[dk, ImageDimensions[trm1rct][[1]]]];
(* extract rectangular region in mediastinum: trm2 *)
trm2 = ImageTrim[igs, {p20, p21}];
(* select pixel values that are larger than zero *)
mat1 = Select[Flatten@ImageData[trm1], # > 0 &];
mat2 = Select[Flatten@ImageData[trm2], # > 0 &];
mean1 = Mean[mat1];
mean2 = Mean[mat2];
max1 = Max[mat1]; max2 = Max[mat2];
min1 = Min[mat1]; min2 = Min[mat2];
std1 = StandardDeviation[mat1]; std2 = StandardDeviation[mat2];
Column[{Show[
HighlightImage[
Image[igs,
ImageSize -> 500], {EdgeForm[{Green, Thickness[Medium]}],
Graphics[Rectangle[p20, p21]]}],
Graphics[{Line[{p10, p11}], {White, Thickness[Small],
Circle[p10, Norm[p10 - p11]]},
Locator[Dynamic[p10], Appearance -> Small,
Background -> LightPink],
Locator[Dynamic[p11], Appearance -> Small,
Background -> LightBlue],
Locator[Dynamic[p20], Appearance -> Small,
Background -> LightPink],
Locator[Dynamic[p21], Appearance -> Small,
Background -> LightBlue]}, PlotRange -> {0, 152},
ImageSize -> 600]],
Grid[{{"", "Mean", "Std dev", "Max", "Min"}, {"Heart", mean1, std1,
max1, min1}, {"Mediastinum", mean2, std2, max2,
min2}, {"H/M Ratio", mean1/mean2, "", "", ""}}, Frame -> All]}]]
|
Applying Machine Learning
We have performed receiver operating characteristic (ROC) analysis to select the most suitable method for modeling the cardiac risk evaluation. By area-under-the-curve (AUC) analysis, using 75% of the data for training and 25% for validation, we have found logistic regression best for our purpose.
Now that we have chosen logistic regression as the method, the rest is simply the generation of a classifier function using Classify in the Wolfram Language. The data to be fed is a set of lists of the form:
![]()
For example:

For this study, we have used data from 105 cases of HFD and 37 cases of ArE from a cohort of CHF patients in Japan. Having randomly chosen 75% of the data to be the training set (trainingSet in the following), the training is done automatically by:

✕
cs = Classify[trainingSet, Method -> "LogisticRegression", ValidationSet -> testSet] |
… where testSet is the test set, i.e. the remaining 25% of the data. (Note that the training and test data cannot be disclosed here, so this section only demonstrates the study’s method.)
Detailed information, e.g. the final value of the loss function and “learning curve,” can be checked with:

✕
Information[cs] |
Now we can evaluate the accuracy and other indices of the classifier with the test set:

✕
measTestc = ClassifierMeasurements[cs, testSet]measTestc[{"Accuracy", "AreaUnderROCCurve"}]
|
When the function ClassifierMeasurements is applied to the training set, it returns:
![]()
This shows that the degree of overfitting is rather mild and the accuracy of 0.827 for the test set is quite high. Not only the value itself, but also the quantitativeness of the risk evaluation is the point. The deviation of a judgement criterion is inevitable as far as we rely on individual human eyes, while we may be able to expect a more quantitative diagnosis for a patient’s condition, when more clinical data is accumulated.
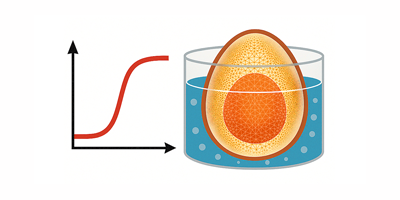
The following figure is the plot of computed probabilities of each class of outcomes as a function of 123I-MIBG HMR, together with other parameters that are made discrete and shown as buttons on the left. The classifier function is the one obtained previously and the plot shown here is a snapshot of the output:

✕
Manipulate[
Plot[{cs[{age, sex, nyha, gfr, ef, hx, wr, hd, isc, hb, bnp, ht, dm},
"Probability" -> "Alive"],
cs[{age, sex, nyha, gfr, ef, hx, wr, hd, isc, hb, bnp, ht, dm},
"Probability" -> "HFD"],
cs[{age, sex, nyha, gfr, ef, hx, wr, hd, isc, hb, bnp, ht, dm},
"Probability" -> "ArE"]}, {hx, 1, 3}, PlotRange -> {0, 1},
PlotLegends -> {"Surviving", "HFD", "ArE"}, GridLines -> Automatic,
AspectRatio -> 1,
LabelStyle -> Directive[Black, 14, ImageResolution -> 480],
AxesLabel -> {"MIBG HMR", "Probability"},
PlotStyle -> {Purple, Blue, Red},
ImageSize -> Medium], {{age, 60.}, {50., 60., 70., 80.}}, {{sex,
"m"}, {"f", "m"}}, {{nyha, 3}, {1., 2., 3., 4.}}, {{gfr,
45.}, {30., 45., 60.}}, {{ef, 35.}, {20., 35., 50.}}, {{wr,
20.}, {0., 20., 40.}}, {{hd, 0.}, {0., 1.}}, {{isc, 1.}, {0.,
1.}}, {{hb, 10.}, {8., 10., 12.}}, {{bnp, 1}, {0., 1., 2., 3.,
4.}}, {{ht, 0.}, {0., 1.}}, {{dm, 0.}, {0., 1.}}]
|
A noteworthy observation here is that the curve for ArE has a peak at an intermediate level of HMR. This tendency has been known only empirically, and our present result verified the speculation based on data. Moreover, although the conditions for this bell-shaped distribution to be realized have been unknown, our analysis sheds light in this respect quantitatively. For instance, such distributions are likely to occur for patients with intermediate New York Heart Association (NYHA) functional classes, which is consistent with the multi-facility research conducted with the data of NYHA classes 2 and 3 (out of 4) in the United States.
Next Steps
With the handiness of not only data manipulation, but also machine learning and the visualization of its results by the Wolfram Language, we were able to obtain a risk evaluation model for estimating the likelihood of death from heart failure and fatal arrhythmic events. The probability of fatal arrhythmic events has been segregated for the first time, especially with respect to the 123I‑MIBG HMR, among other clinical variables.
Since the resulting model is easy to export as an app, we expect that Wolfram Language–based apps or tools could be accessed by those who are in charge of making diagnoses and decisions as to subsequent therapeutic options.
For additional details and deeper analysis of the data and findings, read more about the study in our published paper.
| Check out machine learning courses via Wolfram U or get full access to the latest Wolfram Language functionality with a Mathematica 12.2 or Wolfram|One trial. |
Comments