Number theory is a very old subject that in modern times has branched into various large areas. One of these is additive number theory, with problems like this: when is a prime the sum of two squares? Primes are part of the more classical area now called multiplicative number theory, so as this problem of Fermat’s indicates, the two areas are intimately connected. The problem I discuss in this blog is a mix of additive and multiplicative number theory, with a dash of linear algebra.

Before I give strict definitions, here is the intuitive version of an integer partition via an example: . However, don’t add up! Just think of the sum 14 as being broken up into the four parts: 7, 3, 3, 1. Now the standard additive question is, how many ways are there of breaking 14 into parts? In other words, how many partitions of 14 are there? As we often say, the Wolfram Language has a function for that:

Engage with the code in this post by downloading the Wolfram Notebook

&#10005 PartitionsP[14]

I’ll explain the pieces of the problem at hand as we go along; consider this a succinct abstract:

Two infinite lower-triangular matrices related to integer partitions are inverses of each other. The matrix ν comes from an additive analogue of the multiplicative Möbius μ function, while γ comes from counting generalized complete partitions; a complete partition of n has all possible subsums 1 to n.

Wolfram Language Definitions

First I’ll set up the function definitions we will use.

&#10005 Ferrers@p_ := Framed@Grid[Table["\[FilledCircle]", #] & /@ p]

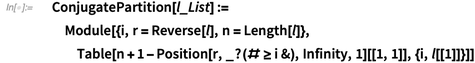
&#10005 ConjugatePartition[l_List] := Module[{i, r = Reverse[l], n = Length[l]}, Table[n + 1 - Position[r, _?(# >= i &), Infinity, 1][[1, 1]], {i, l[[1]]}]]

&#10005 DistinctPartitionQ@x_ := Length@x == Length@Union@x

&#10005 DistinctPartitions@n_ := Select[IntegerPartitions@n, DistinctPartitionQ]

&#10005 PartitionMu@\[Lambda]_ := If[DistinctPartitionQ@\[Lambda], (-1)^Length@\[Lambda], 0]

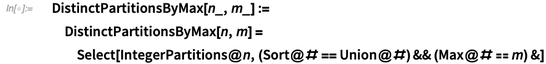
&#10005 DistinctPartitionsByMax[n_, m_] := \!\(TraditionalForm\`DistinctPartitionsByMax\)[n, m] = Select[IntegerPartitions@n, (Sort@# == Union@#) && (Max@# == m) &]

&#10005 PartitionsMuByMax[n_, m_] := PartitionsMuByMax[n, m] = Length@DistinctPartitionsByMax[n, m] - 2 Length@Select[DistinctPartitionsByMax[n, m], EvenQ@*Length]

&#10005 PartitionsMuByMax@r_ := Table[PartitionsMuByMax[i, j], {i, r}, {j, i}]

&#10005 \[Nu]@r_ := PadRight@Table[PartitionsMuByMax[i, j], {i, r}, {j, i}]

&#10005 KStepPartitionQ[\[Lambda]_, k_] := MemberQ[Range@k, Last@\[Lambda]] && And @@ Table[\[Lambda][[j]] - k <= Total@Drop[\[Lambda], First@Last@Position[\[Lambda], \[Lambda][[j]]] ], {j, -1 + Length@\[Lambda]}]

&#10005 KStepPartitionQ[0, _] := {{0}}

&#10005 KStepPartitions[n_, k_] := Select[IntegerPartitions@n, KStepPartitionQ[#, k] &]

&#10005 KStep[0, k_] := 1

&#10005 KStep[n_, k_] := KStep[n, k] = Length@KStepPartitions[n, k]

&#10005 CompletePartitionQ@p_ := KStepPartitionQ[p, 1]

&#10005 CompletePartitions[n_] := KStepPartitions[n, 1]

&#10005 Complete[n_] := KStep[n, 1]

&#10005 pre\[Gamma]@r_ := Table[KStep[i - 1, j - 1], {i, r}, {j, r}]

&#10005 \[Gamma]@r_ := PadRight@Table[KStep[i - j, j - 1], {i, r}, {j, i}]

&#10005 StrictCompositions[n_] := Join @@ Permutations /@ IntegerPartitions[n]

&#10005 StrictCompositionsByMax[n_, m_] := Total[-(-1)^(Length /@ Select[StrictCompositions@n, Max@# == m &])]

&#10005 \[Sigma]@r_ := PadRight@Table[StrictCompositionsByMax[n, m], {n, r}, {m, n}]

&#10005 \[Alpha]@r_ := PadRight@Table[1, {i, r}, {j, i}]

&#10005 \[Chi]@r_ := PadRight@Table[If[Mod[n, k] == 0, MoebiusMu[n/k], 0], {n, r}, {k, n}]

Integer Partitions

Definition of an Integer Partition

Let’s establish the definitions for a multiset and an integer partition:

• A multiset is a collection of elements (like a set) where an element can occur more than once (unlike a set).
• An integer partition of a positive integer is a multiset of positive integers (called its parts) that sum to . In math, we write .

For example, .

In Mathematica, we use a list:

&#10005 {3, 1, 1} // Total

Since the elements of a multiset and a set are unordered, we can arbitrarily choose to order the parts of a partition from largest to smallest. Here are the integer partitions of 5:

&#10005 IntegerPartitions[5]

Here they are again more compactly:

&#10005 Row /@ IntegerPartitions@5

Other Definitions

An older alternative definition is along these lines: “A partition is a way of writing an integer n as a sum of positive integers where the order of the addends is not significant…. By convention, partitions are normally written from largest to smallest addends… for example, 10 = 3 + 2 + 2 + 2 + 1.”

With such a definition, 3 + 2 + 2 + 2 + 1 has to be frozen, because as an arithmetic expression it is 10 and the parts are gone.

Yet another definition: is a partition of if the finite sequence is such that and .

Ferrers Diagram

For each part of a partition , draw a row of dots, then stack the rows:

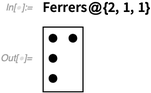
&#10005 Ferrers@{2, 1, 1}

Conjugate Partition

The conjugate partition of a partition is the partition corresponding to the transpose of the Ferrers diagram of :

&#10005 Ferrers@ConjugatePartition@{2, 1, 1}

So is the conjugate partition of , and vice versa.

Distinct Partition

A distinct partition has no repeated part. Here are the four distinct partitions of 6:

&#10005 Row /@ DistinctPartitions@6

The remaining partitions of 6 have repeated parts:

&#10005 Row /@ Complement[IntegerPartitions@6, DistinctPartitions@6]

This is the sequence counting the number of distinct partitions of :

&#10005 PartitionsQ@Range[20]

Generating Functions

Number of Partitions

The number of partitions of is but the next number is not 13:

&#10005 PartitionsP@Range[12]

The generating function for this sequence is:

&#10005 Row[{Sum[PartitionsP@n x^n, {n, 12}], " + \[Ellipsis]"}]

The generating function is equal to the infinite product .

Number of Distinct Partitions

The number of distinct partitions of :

&#10005 PartitionsQ@Range[12]

The generating function for this sequence is:

&#10005 Row[{Sum[PartitionsQ@n x^n, {n, 12}], " + \[Ellipsis]"}]

It is equal to the infinite product .

Two Möbius Functions

Square-Free Numbers

A square-free integer is one that is not divisible by a square greater than 1. Here are the square-free numbers up to 100:

&#10005 Select[Range@100, SquareFreeQ]

Here are numbers up to 100 that are not square free:

&#10005 Select[Range@100, Not@*SquareFreeQ]

Möbius Function μ

In multiplicative number theory, the Möbius μ function is defined on the positive integers as follows:

1. If is not square free, .
2. If is square free, then can be written as the product of distinct primes, for some positive integer . In that case, .

In other words, of a square-free integer is or according to whether has an odd or an even number of prime factors. For example, , , .

Möbius Partition Function μ_P

The function is the partition analogue of the ordinary Möbius function :

&#10005 Text@Grid[{ {"\[Mu]", "\!\(\*SubscriptBox[\(\[Mu]\), \(P\)]\)"}, {, }, {"product", "partition"}, {"primes factors", "parts"}, {"square\[Hyphen]free", "distinct"} }, Alignment -> Left, Dividers -> {{False, True}, {False, True}}]

The definition of :

1. Let if the partition has a repeated part.
2. If the partition has distinct parts and parts in all, .

Here are the partitions of 6 and the corresponding values of the Möbius partition function :

&#10005 Grid[{Row@#, PartitionMu@#} & /@ IntegerPartitions@6, Alignment -> {Right, Left}]

Infinite Triangular Matrices

Pascal’s Triangle

The prime example of an infinite lower-triangular matrix is Pascal’s triangle . Imagine that the rows keep going down and the columns keep going to the right. For readability, let’s replace 0s with dots:

&#10005 MatrixForm[t10 = Table[Binomial[n, k], {n, 0, 9}, {k, 0, 9}], TableAlignments -> Right] /. 0 -> "\[CenterDot]"

Here is the matrix product :

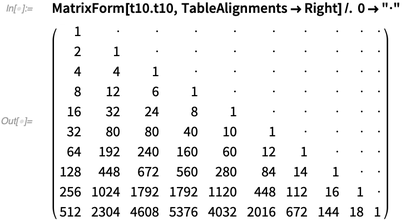
&#10005 MatrixForm[t10.t10, TableAlignments -> Right] /. 0 -> "\[CenterDot]"

Here is the matrix inverse of :

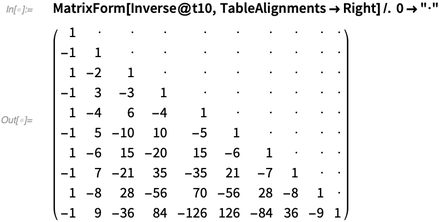
&#10005 MatrixForm[Inverse@t10, TableAlignments -> Right] /. 0 -> "\[CenterDot]"

Stirling Numbers of the First and Second Kind

The Stirling numbers of the first and second kind are another example of a pair of inverse lower-triangular matrices.

A Stirling number of the first kind counts how many permutations of have cycles:

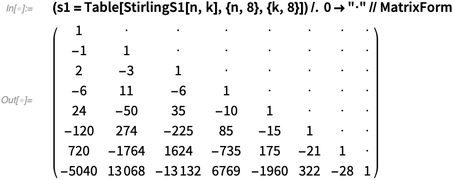
&#10005 (s1 = Table[StirlingS1[n, k], {n, 8}, {k, 8}]) /. 0 -> "\[CenterDot]" // MatrixForm

A set partition of a finite set, say , is a set of disjoint nonempty subsets of .

A Stirling number of the second kind counts how many set partitions of have subsets:

&#10005 (s2 = Table[StirlingS2[n, k], {n, 8}, {k, 8}]) /. 0 -> "\[CenterDot]" // MatrixForm

The two matrices are inverses of each other:

&#10005 Row[{MatrixForm@s1, Style[" \[CenterDot] ", 24], MatrixForm@s2, Style[" = ", 24], MatrixForm[s1.s2]}] /. 0 -> "\[CenterDot]"

Infinite Matrices Can Be Weird

For square matrices and , if , then . As the Demonstration The Derivative and the Integral as Infinite Matrices shows, there are (very familiar) infinite matrices and such that is the identity matrix, but .

Even though infinite lower-triangular matrices with 1s on the main diagonal behave well, we only deal with matrices, where .

Matrix ν

Definition of ν

Define the matrix by , where the sum is over and , .

Here is an alternative definition.

Let be the partitions of into an odd number of parts with maximum part .

Let be the same, except the number of parts should be even.

Let be the number of elements in .

Then , with .

Here is :

&#10005 \[Nu]@10 /. 0 -> "\[CenterDot]" // MatrixForm

To verify that , look at the partitions of 10:

&#10005 Row /@ IntegerPartitions@10

The ones with maximum part 5 are:

&#10005 Select[IntegerPartitions@10, Max@# == 5 &]

Applying to each of those gives:

&#10005 PartitionMu /@ %

Minus the sum is 2, so , as claimed.

Inverse of ν

As Jacobi wrote, “Always invert!” (referring to elliptic integrals). This is :

&#10005 Inverse[\[Nu]@15] /. 0 -> "\[CenterDot]" // MatrixForm

What is the sequence in the second column, ?

You can find the sequence at the OEIS by looking it up. That hits A126796: Number of complete partitions of n, which is a great start in understanding the matrix !

Matrix γ

Subpartitions and Subsums of a Partition

For the matrix γ, let’s look at subpartitions and subsums of a partition. A subpartition of a partition is a submultiset of . For instance, is a subpartition of . A subsum is the sum of a subpartition. So there are eight ( subsums of corresponding to the eight subpartitions of :

&#10005 Text@Grid[ Transpose@{Prepend[Subsets@{3, 1, 1}, "subpartition"], Prepend[Total /@ Subsets@{3, 1, 1}, "subsum"]} ]

Complete Partition

Now let’s look at complete partitions. We define a partition to be complete if it has all possible subsums .

Here are the five complete partitions of 6:

&#10005 Row /@ Select[IntegerPartitions@6, CompletePartitionQ]

And here are the partitions of 6 that are not complete:

&#10005 Row /@ Select[IntegerPartitions@6, Not@*CompletePartitionQ]

This is the sequence counting the number of complete partitions of :

&#10005 Complete /@ Range[0, 10]

Park’s Condition

Consider the partition 7311. We get the subsums 1, 2, 3, 4, 5 easily from 311. But we cannot get 6, so 7311 is not complete.

Qualitatively, if a part is too large relative to the other parts, we cannot get some intermediate subsums. Park’s condition makes this precise.

Theorem (Park): A partition with is complete iff and for each , , .

For example, is not complete (no subsum is 3) because .

Using Park’s condition, it is easy to check—but only if you want!—that the conjugate of a distinct partition is a complete partition.

k-Step Partition

Given a non-negative integer , define a partition to be -step iff and for each , , . Define the empty partition to be the only zero-step partition.

Clearly, a one-step partition is a complete partition:

&#10005 Row /@ CompletePartitions@5

Here are the -step partitions of 5, for :

&#10005 Row /@ KStepPartitions[5, 1]

&#10005 Row /@ KStepPartitions[5, 2]

&#10005 Row /@ KStepPartitions[5, 3]

&#10005 Row /@ KStepPartitions[5, 4]

This is the same as the partitions of 5 with no restrictions:

&#10005 Row /@ KStepPartitions[5, 5]

Matrix of Number of k-Step Partitions

Define to be the number of -step partitions of :

&#10005 pre\[Gamma]@10 /. 0 -> "\[CenterDot]" // MatrixForm

The second column is the number of complete partitions of is .

Definition of γ

Define the matrix by , . In words, the columns of are the number of -step partitions shifted down to form a lower-triangular matrix.

Here is the matrix :

&#10005 \[Gamma]@10 /. 0 -> "\[CenterDot]" // MatrixForm

It matches the inverse of :

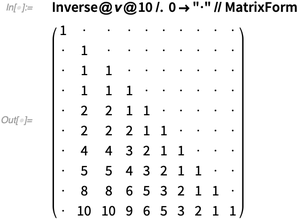
&#10005 Inverse@\[Nu]@10 /. 0 -> "\[CenterDot]" // MatrixForm

Main Theorem

We can now put everything together. The inverse of the matrix matches the matrix , which is the main theorem for this blog.

Theorem. For each , , the identity matrix.

This presents the situation when :

&#10005 Row[{\[Nu]@6 /. 0 -> "\[CenterDot]" // MatrixForm, Style[" \[CenterDot] ", 16], \[Gamma]@6 /. 0 -> "\[CenterDot]" // MatrixForm, Style[" = ", 16], IdentityMatrix@6 /. 0 -> "\[CenterDot]" // MatrixForm}]

Paul Hanna’s Generating Function

Hanna conjectured that

,   (1)

where is the sequence that counts the number of complete partitions of .

Proof: Rewrite the desired identity as

  (2)

or

,   (3)

where the last sum is over all complete partitions of .

We claim every partition contains a maximal complete subpartition. For example, has the maximal complete subpartition . If the maximal subpartition of partitions , then cannot be a part of the original partition . If it were, we could insert it into , contradicting its maximality.

Furthermore, there is no constraint on the parts in larger than because the fact that is missing in means that no larger complete subpartition can be produced. Hence generates all partitions whose maximal complete subpartition is a partition of .

Summing over all gives (3), and consequently (1).

Identifying coefficients for like powers of proves that , the second column of . The straightforward bookkeeping generalization then proves the main theorem for the other columns.

Combinatorial Proof

Here is a proof of the main theorem by example. Consider the dot product of row 10 of with :

&#10005 Row[{MatrixForm@{Last[\[Nu]@10]}, " \[CenterDot] ", MatrixForm@\[Gamma][10][[All, 2]]}]

An entry from is the difference between the number of distinct partitions of odd and even length. Here are these partitions:

&#10005 Table[Row /@ DistinctPartitionsByMax[10, m], {m, 10}]

Here are the complete partitions counted in the third column of :

&#10005 MatrixForm@Join[{{}, {}}, Table[Row /@ CompletePartitions[i], {i, 6}]]

Count them up and recall that the sequence for the number of complete partitions starts like this:

&#10005 Complete /@ Range[6]

Consider the fifth term in the dot product: 2×2. It comes from all possible pairs .

That is:

,

,

,

.

The signs of those pairs are all negative, because the four distinct partitions all have an odd number of parts. Using β, we will find four other terms in the dot product that have the opposite sign to get cancellation.

Involution β

Let be the set of distinct partitions and be the set of complete partitions.

Define the function as follows.

Let and .

1. If is even, then .
2. If is odd, then .

In other words:

1. Add the second-largest part of to the first part and adjoin to .
2. Drop the largest part of from and in , subtract from the largest part and adjoin to .

In the previous example, we had four pairs. Here is how changes them:

,

,

,

.

The resulting pairs are still . However, the odd length becomes an even length, giving the cancellation. Also, reverses itself, so we get complete cancellation.

Formally, the function changes the parity of the length of the distinct partition and is an involution on the set of pairs. Therefore, the dot product is zero.

Compositions

Definition

A composition of is a finite sequence of non-negative integers with sum . So unlike an integer partition, order matters. For example, the two compositions and are different.

Allowing 0 as a part only make sense if the number of parts is specified.

Strict Compositions

A strict composition of is a finite sequence of positive integers with sum . Here are the strict compositions of 4:

&#10005 Row /@ (C4 = StrictCompositions@4)

Let be the number of parts of the composition . Here are the lengths of the compositions just shown:

&#10005 Length /@ C4

Matrix σ

As is for partitions, so is for strict compositions. Let’s define the matrix by , where , . The sum is over all strict compositions of with maximum part and is the number of parts of .

For example, for , , these are the strict compositions:

&#10005 Row /@ Select[C4, Max@# == 2 &]

Three have odd length and one has even length, so .

Just like the matrix before, we define the matrix by , :

&#10005 \[Sigma]@10 /. 0 -> "\[CenterDot]" // Grid

Inverse of σ

Take the inverse of . What are these numbers?

&#10005 Inverse[\[Sigma]@10] /. 0 -> "\[CenterDot]" // Grid

Looking up the second column in the OEIS leads to A002321, which is enough to lead to a conjecture. To formulate it, we define two lower-triangular matrices and .

Matrix α

Let be the lower-triangular matrix of all 1s:

&#10005 \[Alpha]@10 /. 0 -> "\[CenterDot]" // Grid

Matrix χ

Define the lower-triangular matrix by 
 where :

&#10005 \[Chi]@10 /. 0 -> "\[CenterDot]" // Grid

Conjecture

Let’s calculate the matrix product:

&#10005 \[Alpha][10].\[Chi][10].\[Alpha][10] /. 0 -> "\[CenterDot]" // Grid

That matrix product matches the inverse of :

&#10005 Inverse[\[Sigma][10]] /. 0 -> "\[CenterDot]" // Grid

This led me to conjecture that .

Who will prove it?

The relevant OEIS triangles are A134542, A134541, A000012 and A054525.

Conclusion

It is remarkable that the two kinds of partitions should be connected so simply by matrix inversion. That strict compositions are related to the multiplicative Möbius function again via matrix inversion amazes me. Are there more such pairs in the universe of additive number theory?

References

Andrews, G., G. Beck and B. Hopkins. “On a Conjecture of Hanna Connecting Distinct Part and
 Complete Partitions.” Annals of Combinatorics 24 (2020): 217–24.

Brown, J. L. “Note on Complete Sequences of Integers.” The American Mathematical Monthly 68,
 no. 6 (1961): 557–60.

Hoggatt, V. E and C. H. King. “Problem E-1424.” The American Mathematical Monthly
 67 (1960):
 593.

MacMahon, P. A. Combinatory Analysis, vol. 1. Cambridge: Cambridge University Press, 
1915.

OEIS Foundation Inc. (2019), The On-Line Encyclopedia of Integer Sequences, oeis.org.

Park, S. K. “Complete Partitions.” Fibonacci Quarterly 36, no. 4 (1998): 354–60.

Park, S. K. “The r-Complete Partitions.” Discrete Mathematics 183 (1998): 293–97.

Schneider, R. “Arithmetic of Partitions and the q-Bracket Operator.” Proceedings of the 
American
 Mathematical Society 145 (2017): 1953–68.