Introduction

Building on thirty years of research, development and use throughout the world, Mathematica and the Wolfram Language continue to be both designed for the long term and extremely successful in doing computational mathematics. The nearly 6,000 symbols built into the Wolfram Language as of 2016 allow a huge variety of computational objects to be represented and manipulated—from special functions to graphics to geometric regions. In addition, the Wolfram Knowledgebase and its associated entity framework allow hundreds of concrete “things” (e.g. people, cities, foods and planets) to be expressed, manipulated and computed with.

Despite a rapidly and ever-increasing number of domains known to the Wolfram Language, many knowledge domains still await computational representation. In his blog “Computational Knowledge and the Future of Pure Mathematics,” Stephen Wolfram presented a grand vision for the representation of abstract mathematics, known variously as the Computable Archive of Mathematics or Mathematics Heritage Project (MHP). The eventual goal of this project is no less than to render all of the approximately 100 million pages of peer-reviewed research mathematics published over the last several centuries into a computer-readable form.

In today’s blog, we give a glimpse into the future of that vision based on two projects involving the semantic representation of abstract mathematics. By way of further background and motivation for this work, we first briefly discuss an international workshop dedicated to the semantic representation of mathematical knowledge, which took place earlier this year. Next, we present our work on representing the abstract mathematical concepts of function spaces and topological spaces. Finally, we showcase some experimental work on representing the concepts and theorems of general topology in the Wolfram Language.

The Semantic Representation of Mathematical Knowledge Workshop

In February 2016, the Wolfram Foundation, together with the Fields Institute and the IMU/CEIC working group for the creation of a Global Digital Mathematics Library, organized a Semantic Representation of Mathematical Knowledge Workshop designed to pool the knowledge and experience of a small and select group of experts in order to produce agreement on a forward path toward the semantic encoding of all mathematics. This workshop was sponsored by the Alfred P. Sloan Foundation and held at the Fields Institute in Toronto. The workshop included approximately forty participants who met for three days of talks and discussions. Participants included specialists from various fields, including:

• computer algebra
• interactive and automatic proof systems
• mathematical knowledge representation
• foundations of mathematics
• practicing pure mathematics

Among the many accomplished and knowledgeable participants (a complete list of whom, together with the complete schedule of events, may be viewed on the workshop website), Georges Gonthier and Tom Hales shared their experience on the world’s largest extant formal proofs (the Feit–Thompson odd order theorem and the Kepler conjecture, respectively); Harvey Friedman, Dana Scott and Yuri Matiyasevich brought expertise on mathematical foundations, incompleteness and undecidability; Jeremy Avigad and John Harrison shared their knowledge and experience in designing and implementing two of the world’s most powerful theorem provers; Bruno Buchberger and Wieb Bosma contributed extensive knowledge on computational mathematics; Fields Medal winners Stanislav Smirnov and Manjul Bhargava expounded on the needs of practicing mathematicians; and Ingrid Daubechies and Stephen Wolfram shared their thoughts and knowledge on many technical and organizational challenges of the problem as a whole.

As one might imagine, the list of topics discussed at the workshop was quite extensive. In particular, it included type theory, the calculus of constructions, homotopy type theory, mathematical vernacular, partial functions and proof representations, together with many more. The following word cloud, compiled from the text of hundreds of publications by the workshop participants, gives a glimpse of the main topics:

Recordings of workshop presentations can be viewed on the workshop video archive, and a white paper discussing the workshop’s outcomes is also available. In addition, because of the often under-emphasized yet vital importance of the subject for the future development (and practice) of mathematics in the coming decades, 18 participants were interviewed on the technological and scientific needs for achieving such a project, culminating in a 90-minute video (excerpts also available in a 9-minute condensed version) that highlights the visions and thoughts of some of the world’s most important practitioners. We thank filmmaker Amy Young for volunteering her time and talents in the compilation and production of this unique glimpse into the thoughts of renowned mathematicians and computer scientists from around the world, which we sincerely hope other viewers will find as inspiring and enlightening as we do.

Computational Encoding of Function Spaces

The eCF project encoded continued fraction terminology, theorems, literature and identities in computational form, demonstrating that Wolfram|Alpha and the Wolfram Language provide a powerful framework for representing, exposing and manipulating mathematical knowledge.

While the theory of continued fractions contains both high-level and abstract mathematics, it represents only a tiny first step toward Stephen Wolfram’s grand vision for computational access to all of mathematics and the dynamic use of mathematical knowledge. Our next step down this challenging path therefore sought to encode within the Wolfram Language and Wolfram|Alpha entity-property framework a domain of more abstract and inhomogeneous mathematical objects having nontrivial properties and relations. The domain chosen for this next step was the important and fairly abstract branch of mathematics known as functional analysis.

That step posed a number of new challenges, among them the need for graduate-level mathematical knowledge in the domain of interest, formulation of entity names that “naturally” contain parameters and encode additional information (say, measure spaces) and the introduction of stub extensions to the Wolfram Language.

Work was carried out from December 2014–July 2016 and consisted of knowledge curation in three interconnected knowledge domains: "FunctionSpace", "TopologicalSpaceType" and "FunctionalAnalysisSource", together with the development of framework extensions to support them. This functionality was recently made available through the Wolfram Language entity framework and consists of the following content:

• 126 function spaces (many parametrized); 45 properties
• 39 topological space types; 14 properties
• 147 functional analysis sources; 49 properties

Full availability on the Wolfram|Alpha website is expected by early January 2017.

Function Spaces

Two underlying concepts in functional analysis are those of the function space and the topological space. A function space is a set of functions of a given kind from one set to another. Common examples of function spaces include L^p spaces (Lebesgue spaces; defined using a natural generalization of the p-norm for finite-dimensional vector spaces) and C^k spaces (consisting of functions whose derivatives exist and are continuous up to k^th order).

As a simple first example in accessing this functionality, we can use RandomEntity to return a sample list of function spaces:

Similarly, EntityValue can be used to access curated properties for a given space:

As can be seen in various properties in this table, some mathematical representations required the introduction of new symbols not (yet) present in the Wolfram Language. This was accomplished by introducing them into a special PureMath` context. For example, after evaluating the above table, the following “pure math extension symbols” appear:

For now, these constructs are just representational. However, they are not merely placeholders for mathematical concepts/computational structures, but also have the benefit of enhancing human readability by automatically adding traditional mathematical typesetting and annotations. This can be seen, for example, by comparing the raw semantic expressions in the table above with those displayed on the Wolfram|Alpha website:

In the longer term, many such concepts may be instantiated in the Wolfram Language itself. As a result, both this and any similar semantic projects to follow will help guide the inclusion and implementation of computational mathematical functionality within Mathematica and the Wolfram Language.

A slightly more involved example demonstrates how the entity framework can be used to construct programmatic queries. Here, we obtain a list of all curated function spaces associated with mathematician David Hilbert:

One interesting property from the table above that warrants a bit more scrutiny is "RelationshipGraph". This consists of a hierarchical directed graph connecting all curated topological space types, where nodes A and B are connected by a directed edge A↦B if and only if “S is a topological space of type A” implies “S is a topological space of type B”, and with the additional constraint that all nodes are connected only via paths maximizing the number of intermediate nodes. For each function space, this graph also indicates (in red) topological space types to which a given space belongs. For example, the Lebesgue space L² has the following relationship graph:

Here we show a similar graph in a slightly more streamlined and schematic form:

This graph corresponds to the following topological space type memberships:

While portions of this graph appear in the literature, the above graph represents, to our knowledge, the most complete synthesis of the hierarchical structure of topological vector spaces available. (The preceding notwithstanding, it is important to keep in mind that the detailed structure depends on the detailed conventions adopted in the definitions of various topological spaces—conventions that are not uniform across the literature.) A number of interesting facts can be gleaned from the graph. In particular, it can immediately be seen that the well-known Hilbert and Banach spaces (which have high-level structural properties whose relaxations lead to more general spaces) fall at the top of the hierarchical heap together with “inner product space.” On the other hand, topological vector spaces are the “most generic” types in some heuristic sense.

During the curation process, we have taken great care that function space properties are correct for all parameter values. This can be illustrated using code like the following to generate a tab view of Lebesgue spaces for various values of its parameter p and noting how properties adjust accordingly:

One of the beautiful things about computational encoding (and part of the reason it is so desirable for mathematics as a whole) is that known results can be easily tested or verified. (Similarly, and maybe even more importantly, new propositions can be easily formulated and explored.) As an example, consider the duality of Lebesgue spaces L^p and L^q for 1/p+1/q=1 with p≥1. First, define a variable to represent the L^p entity:

Now, use the "DualSpace" property (which may be specified either as a string or via a fully qualified EntityProperty["FunctionSpace", "DualSpace"] object, the latter of which may be given directly in that form or the corresponding formatted form ) to obtain the dual entity:

As can be seen, this formulation allows computation to be performed and expressed through the elegant paradigm of symbolic transformation of the entity canonical name. Taking the dual space of L^q in turn then gives:

Finally, applying symbolic simplification to the entity canonical name:

This verifies we have obtained the same space we originally started with:

In other words, that the double dual (L^p)^**, where * denotes the dual space, is equivalent to L^p. (Function spaces with this property are said to be reflexive.)

It is also important to emphasize that the curation of the existing literature on function spaces is not always straightforward, as illustrated in particular by the myriad of (mutually conflicting) conventions used for the interrelated collection of function spaces known as Campanato–Morrey spaces:

This challenge is made clear with the following table, whose creation required a meticulous study of the literature:

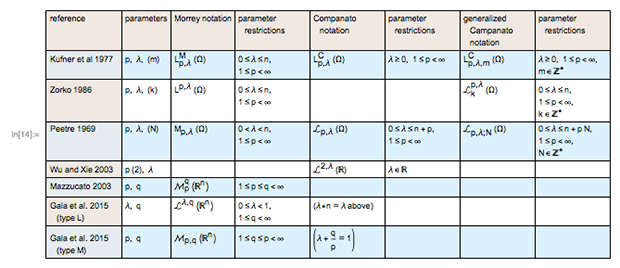
As a result of multiple conventions, we chose in cases like this to include multiple, separate entities that are equivalent under appropriate (but possibly nontrivial) transformations of parameters and notations. For example:

Topological Space Types

A topological space may be defined as a set of points and neighborhoods for each point satisfying a set of axioms relating the points and neighborhoods. The definition of a topological space relies only upon set theory and is the most general notion of a mathematical space that allows for the definition of concepts such as continuity, connectedness and convergence. Other spaces, such as manifolds and metric spaces, are specializations of topological spaces with extra structures or constraints. Common examples of topological vector spaces include the Banach space (a complete normed vector space) and the Hilbert space (an abstract Banach space possessing the structure of an inner product that allows length and angle to be measured). Topological spaces could be considered more abstract than function spaces (e.g. they are typically defined based on the existence of a norm as opposed to having a definite value for their norm). Being so general, topological spaces are a central unifying notion and appear in virtually every branch of modern mathematics. The branch of mathematics that studies topological spaces in their own right is called point-set topology or general topology.

EntityList can be used to see a complete list of curated topological space types:

Similarly, EntityValue[space type, "PropertyAssociation"] returns all curated properties for a given space:

While more could be said and done with topological space types, in this project this domain was primarily used as a convenient way to classify function spaces. However, as the second project to be discussed in this blog will show, additional exploratory work is currently being done that could result in the augmentation of the human- (but not computer-) readable descriptions of topological spaces with semantically encoded versions potentially even suitable for use with automated proof assistants or theorem provers.

Functional Analysis Sources

A final component added in this project was a set of cross-linked literature references that provide provenance and documentation for the various conventions (definitions etc.) adopted in our curated functional analysis datasets. These references can be searched based on the journal in which a paper appears, the year or decade it was published, the author or the language in which it was written:

• functional analysis papers in Crelle’s journal
• functional analysis papers from the 1940s
• functional analysis works by Grothendieck
• Besov’s 1959 functional analysis paper
• functional analysis papers in Italian

For mathematicians who wish to explore the source of the data down to the page (theorem etc.) level, this information has also been encoded:

Finally, we can use this detailed reference information in a way that provides a convenient overview of both existing notational conventions and those we adopted in this project:

Encoding of Concepts and Theorems from Topology

The second project we discuss in this blog is the not-unrelated augmentation of the Wolfram Language to precisely represent the definitions of mathematical concepts, statements and proofs in the field of point-set topology. This was done by creating an “entity store” for general topology consisting of concepts and theorems curated from the second edition of James Munkres’s popular Topology textbook. Although this project did not construct an explicit proof language (suitable, say, for use by a proof assistant or automated theorem prover), it did result in the comprehensive representation of 216 concepts and 225 theorems from a standard mathematical text, which is a prelude to any work involving machine proof.

EntityStore is a function introduced in Version 11 of the Wolfram Language that allows custom entity-property data to be packaged, placed in the cloud via the Wolfram Data Repository and then conveniently loaded and used. To load and use the general topology entity store, first access it via its ResourceData handle, then make it available in the Wolfram Language by prepending it to the list of known entity stores contained in the global $EntityStores variable:

As can be seen in the output, a nice summary blob shows the contents of the registered stores (in this case, a list containing the single store we just registered), including the counts of entities and properties in each of its constituent domains. Now that the entity store is registered, the custom entities it contains can be used within the Wolfram Language entity framework just as if they were built in. For example:

Similarly, we can see a full list of currently supported properties for topological theorems using EntityValue:

Before proceeding, we perform a little context path manipulation to make output symbols format more concisely (slightly deferring a discussion of why we do this until the end of this section):

A nice summary table can now be generated to show basic information about a given theorem:

"InputFormSummaryGrid" displays the same information as "SummaryGrid", but without applying the formatting rules we’ve used to make the concepts and theorems easily readable. It’s a good way to see the exact internal representation of the data associated with the entity. This can help us to understand what is going on when the formatting rules obscure this structure:

While it’s pretty straightforward to understand the mathematical assertion being made here, let’s look at each property in detail. Here, for example, is the display name (“label”) used for the entity representing the above theorem in the entity store, formatted using InputForm to display quotes explicitly and thus emphasize that the label is a string:

Similarly, here are alternate ways of referring to the theorem:

… the universally quantified variables appearing at the top level of the theorem statement (i.e. these are the variables representing the objects that the theorem is “about”):

… the conditions these objects must satisfy in order for the theorem to apply:

… and the conclusion of the theorem:

Of course, we could have just as easily listed Math["IsHausdorff"][Χ] as a restriction to this theorem and Math["IsT1"][Χ] as the statement since the manner in which the hypotheses are split between "Restrictions" and "Statement" is not unique. However, while the details of the splitting are subject to style and readability, the mathematical content of the theorem as expressed through any of these subjective choices is equivalent.

Finally, we can retrieve metadata about the source from which the theorem was curated:

Now, backing up a bit, you may well wonder about expressions with structures such as Category[...] and Math[...] that you’ve seen above. Let’s take a look at one of them, but this time through a general topology concept instead of a theorem:

Some of these properties are shared with corresponding properties for theorems:

You can see the common properties by intersecting the full lists of supported properties for concepts and theorems:

While properties are similar across topology theorems and concepts, there are some differences that should be addressed. "Arguments" for a concept takes the role of "QualifyingObjects" for a theorem. Just as theorems are thought of as applying to certain objects, concepts are thought of as functions that can be applied to certain objects. The output can be a Boolean value, as in this case. We would call such a concept a property or a predicate. Other concepts represent mathematical structures. For example, Math["MetricTopology"] takes a metric space as an argument and outputs the corresponding topology induced by the metric. The entity that corresponds to this math concept is .

A "Restrictions" property for concepts is very similar to the corresponding property for theorems. And just as in the case with theorems, there’s nothing in principle stopping us from moving this condition from "Restrictions" and conjoining it to the output. The difference is that this can always be done for theorems, but it can only be done for concepts representing properties since the output is interpreted as having a truth value:

Finally, the "Output" property here gives the value of the expression Math["IsHausdorff"][X]:

When we use such an expression in a theorem or in the definition of another concept, we interpret it as equivalent to what we see in "Output". As we know, stating and understanding mathematics is much easier when we have such shorthands than if all theorems were stated in terms of atomic symbols and basic axioms.

Two of the most exciting properties on this list are "RelatedConcepts" and "RelatedTheorems". One of our goals is to represent mathematical concepts and theorems in a maximally computable way, and these are just an example of some of the computations we hope to do with these entities. A concept appears in "RelatedConcepts" if it is used in the "Restrictions", "Notation" or "Output" of a concept or the "Restrictions", "Notation" or "Statement" of a theorem. A theorem appears in the "RelatedTheorems" of a concept if that concept appears in the "RelatedConcepts" of that theorem. With this in mind, take a closer look at the examples above:

It is important to emphasize that these relations were not curated, but rather computed, which is possible because of the precise, consistent and expressive language used to encode the concepts and theorems. As a matter of convenience, however, they’ve been precomputed for speed to allow you to, say, easily find the definition of concepts appearing in a theorem.

As an example of the power of this approach, we can use the Wolfram Language’s graph functionality to easily analyze the connectivity and structure of the network of topological theorems and concepts in our corpus:

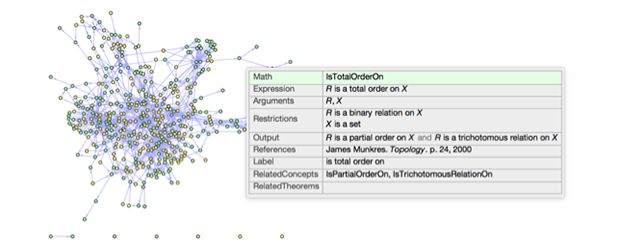
As was the case for topological spaces, a number of extension symbols to the Wolfram Language were introduced in this project. We already encountered the Math and Theorem extensions, but there are also a number of others. For now, they have been placed in a GeneralTopology` context (analogous to the PureMath` context introduced for function spaces). This can be verified by examining the context of such symbols, e.g.:

The motivation behind appending GeneralTopology` to our context path is also now revealed, namely to suppress verbose context formatting in our outputs (so we will see things like Math instead of GeneralTopology`Math). Here is a complete listing of language extensions introduced in the GeneralTopology` context:

Again—as was the case for language extensions introduced for function spaces—some of these may eventually find their way into the Wolfram Language. However, independent of such considerations, these two small projects already show the need for some kind of infrastructure that allows incorporation, sharing and alignment of language extensions from different—and likely independently curated—domains.

We close with some experimental tidbits used to enhance the readability and usability of the concepts and theorems in our entity store. You have probably already noted the nice formatting in "SummaryGrid" and possibly even wondered how it was achieved. The answer is that it was produced using a set of MakeBoxes assignments packaged inside the entity store via the property EntityValue["GeneralTopologyTheorem", "TraditionalFormMakeBoxAssignments"]. Similarly, in order to provide usage messages for the GeneralTopology` symbols (which must be defined prior to having messages associated with them), we have packaged the messages in the special experimental EntityValue["GeneralTopologyTheorem", "Activate"] property, which can be activated as follows:

The result is the instantiation of standard Mathematica-style usage messages such as:

While the eventual implementation details of such features into a standard framework remains the subject of ongoing design and technical discussions, the ease with which it is possible to experiment with such functionality (and to implement semantic representation of mathematical structures in general) is a testament to the power and flexibility of the Wolfram Language as a development and prototyping tool.

Conclusion

These projects undertaken at Wolfram Research during the last year have explored the semantic representation of abstract mathematics. In order to facilitate experimentation with this functionality, we have posted two small notebooks to the cloud (function space entity domain and the topology entity store) that allow interactive exploration and evaluation without the need to install a local copy of Mathematica. We welcome your feedback, comments and even collaboration in these efforts to extend and push the limits of the mathematics that can be represented and computed.

As a final note, we would like to emphasize that significant portions of the work discussed here were carried out as a part of internship projects. If you know or are a motivated mathematics or computer science student who is interested in trying to break new ground in the semantic representation of mathematics, please consider 1) learning the Wolfram Language (which, since you are reading this, you may well have already) and 2) joining the Wolfram internship program next summer!