“What are the odds?” This phrase is often tossed around to point out seemingly coincidental occurrences, and it’s normally intended as a rhetorical question. Most people won’t even wager a guess; they know that the implied answer is usually “very slim.”

However, I always find myself fascinated by this question. I like to think about the events leading up to a situation and what sorts of unseen mechanisms might be at work. I interpret the question as a challenge, an exciting topic worthy of discussion. In some cases the odds may seem incalculable—and I’ll admit it’s not always easy. However, a quick investigation of the surrounding mathematics can give you a lot of insight. Hopefully after reading this post, you’ll have a better answer the next time someone asks, “What are the odds?”

But before we go more in depth about odds, it’s important to touch on the more general topic of probability.

Probability theory incorporates many ideas on how random events play out, including many functions (distributions) that describe such phenomena mathematically. Although the subject can get quite complex, the basic strategy for estimating an event’s probability involves counting up the possible outcomes and determining all the ways each outcome can occur.

In the simple example of flipping a coin, this process is almost trivial. As long as the coin is “fair” (i.e. not altered in a way that favors a particular result), it will come up either heads or tails each time, and each outcome can only occur one way. You could easily create a coinFlip function to model this behavior:

Now imagine this situation with two coins. Each coin still has the same equal chance of coming up heads or tails. There are now four equally likely outcomes:

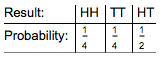
Each result has a probability of 1/4, or 25%. But if we treat the two mixed cases (TH and HT) as equivalent (i.e. one head and one tail), our interpretation changes. Now we have a 1/4 chance of getting both heads (or both tails), and a 2/4=1/2 chance of getting one head and one tail:

In either case—and, indeed, in all cases—the sum of these probabilities is 1. Also note that the probability of getting two heads in a row is the same as the product of the probabilities of getting a head for each toss: 1/2 * 1/2=1/4. When predicting a specific series of events (in this case, a head followed by another head), the probabilities are multiplied. This means that as the number of successive predictions grows, the probability of being correct diminishes. This seems sensible, since nobody can be right all the time:

It’s common to interpret probability in terms of chances. A probability of 1/4 can be read as a 1 in 4 chance of an event happening. Indeed, many people will quote this type of figure as “the odds of” an event happening, though this is technically incorrect. Here are the chances of drawing any of the possible hands in five-card draw poker:

Odds are a slightly different representation of probability often used in games and wagering situations. Whereas chances are expressed as a ratio of the number of ways an event will occur versus all possible outcomes, odds are expressed as a ratio of the number of ways an event will occur versus the number of ways it won’t occur—a comparison of wins to losses. This may either be formulated as odds in favor (wins/losses) or odds against (losses/wins):

In the single coin flip example, the odds in favor of landing on heads are 1 to 1—either it will turn up heads (the first 1) or it won’t (the second 1). In a double coin flip, your odds against getting two heads (HH in the chart above) are 3 to 1:

Since both are expressed as ratios of simple numbers, chances and odds notation can be especially useful for non-mathematical types. For instance, the chances of winning the recent $1.6B Powerball jackpot were stated as 1 in 292,201,338. In other words, the odds against winning are 292,201,337 to 1. These odds are based on the process for the drawing—choose 5 of the 69 white balls and 1 of the 26 Powerballs. Here Binomial[n,k] is the Wolfram Language function for a combination (the probability of choosing k specific items out of n available choices), and the chance of getting all 5 white balls is multiplied by the chance of getting the Powerball:

Since only one of the possibilities (out of 292,201,338 total) results in a win, the total odds against are 292,201,337 to 1. To put this in perspective, the odds of being dealt a royal flush (the rarest hand in poker) are much better. There are only four possible ways to get this hand, out of the ~2.5 million unique hands that can be drawn:

Clearly, having nearly 300 million ways to lose is less appealing than having 600 thousand. With such large numbers it’s easy to see why odds and chances are often interchanged—the ratios are almost exactly the same, because almost all of the possibilities are considered losses. In either case, a small proportion of wins means a small chance of winning. Simple enough, right?

In many cases where one might run into this “odds” notation, it’s not exactly clear where the numbers are coming from. What are the odds of a particular team winning the Super Bowl? While it can be easy to find quotes for such figures (FiveThirtyEight currently has Carolina at 3 to 2 against Denver), it’s much more difficult to figure out how they came to be.

This brings us to another important subject: statistics. It turns out that while random events are difficult to predict, long-term trends and patterns emerge over time that can help shape our predictions. Statistics is the discipline of collecting and organizing data—usually in large quantities—in order to create a model.

Team and player ratings in most sports are based on historical statistics such as batting average, passing yards, goals blocked, etc. Since sports (and many other competitive activities such as board games) are a precarious mashup of chance and skill, trends are often difficult to pin down through casual observation. This is the reason that betting situations (most recently daily fantasy sports) are often swept by folks with an understanding of both probability and statistics.

But for now, let’s get back to our coin. It seems intuitive that any series of coin flips ought to come out (about) half heads, half tails. To test this assumption, we can simulate a series of coin flips, tallying up the results:

Results vary, but usually it’s pretty close. Why is this?

Mathematically, you can think of the coin flip as a random choice between 0 (tails) and 1 (heads), with the expectation that you’ll get each value about half the time. This puts the expected value of a single coin flip at 1/2, or 0.5.

Let’s set up a function using this model, along with a way to visualize the results of those trials:

Looking at a series of ten or twenty flips might not be sufficient; each flip is independent, so it’s quite possible to come up mostly heads or mostly tails:

It is, as they say, anyone’s guess. However, after flipping the coin hundreds or thousands of times, you’ll start to notice the data converging on a pattern:

In this series, you see what is known as the law of large numbers, which states that the average value of repeated trials in a particular system (the solid blue line) should tend toward the expected value of a single trial (the dotted red line). In this case, you should get an average of around 0.5—a trend clearly shown by the graphs.

The takeaway here is that the system’s long-term behavior is much more important than any small-scale effects. Also, regardless of any short-term trends, the probability of the next flip coming up heads is still just 50%. The mistaken belief that a period of frequent “heads” results will increase the chances of flipping “tails” the next time is known as the gambler’s fallacy.

Sports fans may be familiar with a related pitfall: when an athlete has a “hot streak” during a particular match, many fans are inclined to believe the streak will continue (as though by some sort of cosmic momentum). Most often, this is not the case, and it can be detrimental to one trying to predict an outcome. This is in part because the prediction of multiple events must also take into account whether the events are related or, in mathematical terms, whether the variables are independent.

In our coin example, it’s clear that the outcome of one flip should not affect the next. In more complex cases, it may not be easy to tell.

Consider actuarial science, for example. The insurance industry bases its entire model around assessment of the risks involved in various activities. They sift through a lot of data to find long-term patterns in risky behavior. It’s an actuary’s job to know that you’re more likely to be struck by lightning than to die in a plane crash (though, fortunately, we have Wolfram|Alpha for that). As morbid as this field may seem, it increases our collective understanding of risk. Indeed, these risk assessment models can often shape government policies.

Of course, statistics don’t have to be too serious. You can try to estimate the chances of really fun stuff like alien life in our galaxy. Or calculate the odds of at least two people in the room sharing a birthday (a favorite at parties). The possibilities are endless, so the odds are pretty low that you’ll run out of ideas anytime soon.

Download this post as a Computable Document Format (CDF) file.