Solving the Knight’s Tour on and off the Chess Board
I first came across the knight’s tour problem in the early ’80s when a performer on the BBC’s The Paul Daniels Magic Show demonstrated that he could find a route for a knight to visit every square on the chess board, once and only once, from a random start point chosen by the audience. Of course, the act was mostly showmanship, but it was a few years before I realized that he had simply memorized a closed (or reentrant) tour (one that ended back where he started), so whatever the audience chose, he could continue the same sequence from that point.
In college a few years later, I spent some hours trying, and failing, to find any knight’s tour, using pencil and paper in various systematic and haphazard ways. And for no particular reason, this memory came to me while I was driving to work today, along with the realization that the problem can be reduced to finding a Hamiltonian cycle—a closed path that visits every vertex—of the graph of possible knight moves. Something that is easy to do in Mathematica. Here is how.
The first thing that we have to do is construct the graph of knight moves. A knight can move to eight possible squares in the open, but as few as two in the corners. But if you ignore that and think of when you were taught chess, you were probably told that a knight could move along two and across one, or vice versa. This gives the knight the property that it always moves a EuclideanDistance of √5. We can use this test to construct the edges of our graph from the list of all possible pairs of positions.
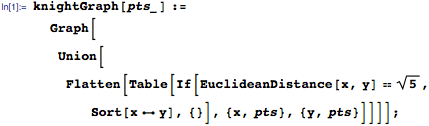
Sorting removes unhelpful multiple edges that just slow the computation down. Ignoring chess conventions, I choose x and y to both take values 1–8 (rather than x being from A to H).

Now that we have the graph, we can find a tour.
Which looks very nice visualized on a chess board.
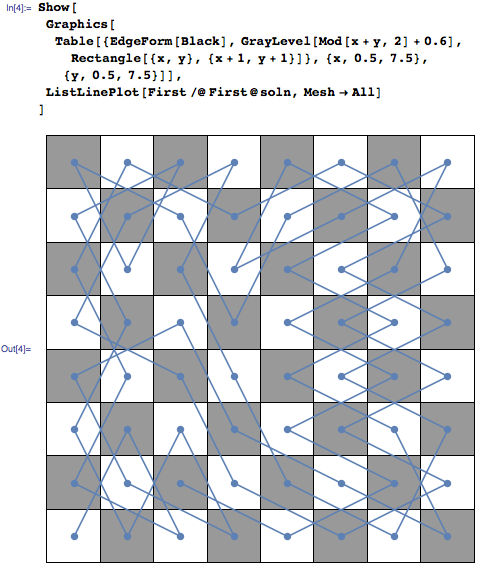
I understand that this problem is often used as an exercise in computer science courses, and you can find some iterative solutions and specific solutions at demonstrations.wolfram.com. But at four lines, this graph theory solution isn’t too much of a challenge. Indeed, it seemed a little unsatisfying to stop here.
Giving FindHamiltonianCycle a second argument finds more than one tour. But scrolling through a notebook of the first 1,000 didn’t reveal anything interesting. And the properties of differently sized chess boards have been well studied. So I decided to extend the idea in a slightly more whimsical way.
Oddly, all the definitions of a knight’s tour that I found on the web assume a rectangular space. Indeed, Mathematica contains a built-in function KnightTourGraph, which does roughly the same as my knightGraph function, but assumes a rectangular grid. But if I bring in Mathematica‘s image processing, it is easy to generate the knight’s tour graph over points in non-rectangular shapes, like this:
First I Binarize the pixels of some source image. The knight is allowed to visit the black pixels in the result, but not the white. Then I get the coordinates of the black pixels and map them to the coordinate space of my plotting function.

Now I just solve and plot that graph as before, but this time visualize with the black pixels, instead of a chess-board grid.

It turns out that most irregular shapes do not have a closed knight’s tour, but messing around with the image size can find exceptions. So a bit of search code is needed. This one takes a single character, rasterizes it at different font sizes, and returns the size for which a tour exists. The Monitor part lets you watch the progress; tour finding scales poorly and can get very slow if you let the font sizes grow too big.

Let’s start by searching simple filled circles.
![]()
So out of the 42 sizes tested, only these 5 have solutions. The smaller, more crowded font sizes produce more irregular tour paths.

But larger image sizes make the shape more recognizable.

Playing around with other characters is amusing for a while. Here is the letter “o” in 34 point:

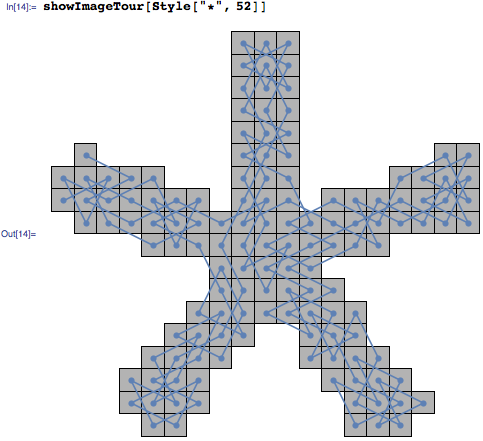
An asterisk at 52 point:
And since chess puts us firmly in the “games” space, here are some playing card suits:


And finally my rendition of Pacman:
Feel free to share any interesting discoveries in the comments section.
Download this post as a Computable Document Format (CDF) file.



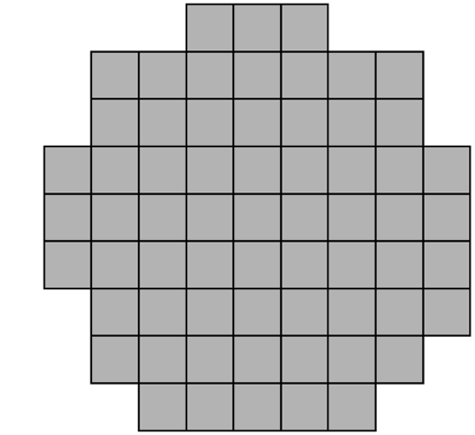
I think it should be pointed out that the tour computed for the club-shaped board is not strictly valid. One of the knight jumps requires it to move off the board and two squares are not visited.
Well spotted, I didn’t notice that!
I think this should be fixed by replacing “Graph[” line in knightGraph with “Graph[pts,”, which includes all vertices in the definition of a graph – which again makes it impossible knight’s tour to succeed as vertices without edges are impossible to visit.
While it was pointed out to me, during proof reading, that there would be objections about the knight jumping over a gap, I consider that a valid move. I have always though of the knight as a “flying” piece. It doesn’t care about pieces in the way, so shouldn’t care about gap.
However, we all missed my bug that you point out about the unvisited squares. The cause was correctly diagnosed by kirma in the next comment.
The fix is to change knightGraph to ensure that all the points are vertices of the output Graph even if they are not connected. I think just adding pts as the first argument for Graph will do it…
knightGraph[pts_] := Graph[pts,
Union[Flatten[Table[If[EuclideanDistance[x, y] == Sqrt[5],
Sort[UndirectedEdge[x, y]], {}], {x, pts}, {y,
pts}]]]];
In the case of the ClubSuit it will now return an unconnected Graph which is unsolvable.
A small note: knightGraph constructs an incorrect graph for Hamiltonian cycle checking if one or more of the points involved have no neighbours at a distance of Sqrt[5]. This makes FindHamiltonianCycle find tours that actually don’t visit every specified square.
Additional checking for such squares is easy, though.
Interesting timing. I just posted about Knight’s Tour literally minutes ago (using a simple backtracking solution):
https://blog.jverkamp.com/2014/09/04/chess-puzzles-knights-tour/
Generating arbitrary boards from images is a really cool idea though. I may have to borrow that. :)
Mike Dupuis and I, with the help of Mathematica, recently characterized all rectangular boards for which the knight graph is “laceable”: there is a Ham. path from any point to any other point (of opposite color).
For the 8×8 I have ALL the paths in a demo at http://demonstrations.wolfram.com/LaceableKnightGraphs/
The paper is at http://amc-journal.eu/index.php/amc/issue/view/22 (last item)
A very difficult magic trick is to ask someone to pick one white and one black square and make a Ham. path from one to the other!
A paper about similar things in the game of hex chess will appear soon in College Math Journal: lots of nice open questions.
Thanks for a great blog on a fascinating topic. Some similar work sits in the archives; use of shapes has been explored by Ryohei Miyadera, et al.,
http://library.wolfram.com/infocenter/MathSource/6714/ but the ability to use symbols to generate board shapes is neat. The work by Arnd Roth, http://library.wolfram.com/infocenter/MathSource/909/ is also interesting, but his use of symmetry and Euclidean distance in his algorithm leads to it being weak when there are asymmetric board shapes.
The results of searching for suitable point sizes depends on the monitor settings; my dated equipment gives
In[29]:=characterSizeFinder[“*”, 60]
Out[29]= {13, 14}
whereas the blog gives a result for point size of 52. Can the code be altered to give results independent of hardware?
The font used is the culprit giving different results for differing point size, so the monitor lives to display another session.
How would I calculate all the knight’s tours for a 6×28 matrix?