Analyzing Your Email with Mathematica
In Stephen Wolfram’s recent blog post about personal analytics, he showed a number of plots generated by analyzing his archive of personal data. One of the most common pieces of feedback we received was that people wanted to know how they could perform the same kind of analysis on their own data. So in this blog post I’m going to show you how to analyze your email the same way Stephen Wolfram did.
Naturally, we did all the data cleaning and analysis for Stephen’s data in Mathematica, so we’ll be using Mathematica for everything here as well. All the code can be downloaded here.
Let’s start with that really cool diurnal plot Stephen did of his outgoing email. This plot shows the date and time each email was sent, with years running along the x axis and times of day on the y axis:

To make this plot, we first need to import our email into Mathematica. There are lots of ways to do this, depending on the details of your email server and so on, but for the purposes of this blog post I’ve written a simple function that imports mail from an IMAP mail server:

This function uses J/Link to call the JavaMail library, included in the download, for connecting to your mailbox and downloading emails from it.
You call the function with the name of the IMAP server and the name of the mail folder you want to import mail from. Here I’m importing the emails from my Sent Mail folder in my Gmail account:
![sentdates = importemaildates["imap.gmail.com", "[Gmail]/Sent Mail"]; Importing email ... please wait ... Finished importing email! sentdates = importemaildates["imap.gmail.com", "[Gmail]/Sent Mail"]; Importing email ... please wait ... Finished importing email!](https://content.wolfram.com/sites/39/2012/04/Email-In4.png)
When you evaluate this line, a dialog window will pop up that asks you for your email address and password:

After entering your email address and password in the input fields, the function will return a list of dates that were parsed from the time stamps on each email:
![]()
![]()
![]()

I’ll do the same thing for my incoming mail, this time specifying the folder name Inbox:
![incomingdates = importemaildates["imap.gmail.com", "Inbox"]; Importing email ... please wait ... Finished importing email! incomingdates = importemaildates["imap.gmail.com", "Inbox"]; Importing email ... please wait ... Finished importing email!](https://content.wolfram.com/sites/39/2012/04/Email-In7.png)
![]()
![]()
![]()

Now that we have the email time stamps, we can reproduce almost every single plot in Stephen’s blog post!
Let’s start with the diurnal plot. Here’s a function that takes a list of dates and uses the function DateListPlot to plot a point for each email sent:
![]()

![]()

Clearly I send a lot less email than Stephen Wolfram does! Still, there are some patterns visible here. The density is clearly higher around 2007–2008, with a rather sharp looking drop-off in mid-2008 (hmm, what happened in mid-2008?). There is a well-defined “sleep band” in the plot from around 1am to 9am or so, as I would expect, but I clearly sent less mail after midnight after around 2010. And now that I think about it, that’s right around when I started going to the gym in the mornings, so that makes sense.
The little burst of emails that are being sent in the middle of the night in mid-2009 aren’t actually a period of insomnia: I was in Italy lecturing at the 2009 Wolfram Science Summer School, so my time zone was shifted by +7 hours. Since I didn’t bother to change the time zone in my Gmail settings while I was away, all the emails I sent continued to be stamped with my regular time zone. So if I sent mail at midnight in Italy, the email time stamp said something like 5am local time.
Let’s see what my incoming mail looks like:
![]()

I receive a LOT more email than I send! There are some interesting patterns here as well. One obvious feature is the daily automated emails I received for certain periods of time, which appear as perfectly straight streaks in the diurnal plot, since they get sent automatically at the same time of day each day.
Now I want to compare the number of emails I’ve sent and received as a function of time. So let’s use DateListPlot again to plot the time series of incoming and outgoing emails superimposed (the code for this plot and all subsequent plots is in the attached notebook):
![]()

There’s definitely a correlation between the number of incoming and outgoing emails at any given time: when incoming email is high, outgoing tends to be high as well. That’s probably because when I receive more emails, I send more emails in response (as opposed to me initiating more discussions and causing more incoming replies)—but to find out for sure I’d need to analyze the email threads in detail.
We can also plot the daily incoming and outgoing mail with the monthly average:
![]()

![]()

These time series plots show my emailing behavior on timescales of years, but we can also look at the distribution of emails sent by time of day. Here’s the daily distribution for my sent mail:
![]()

It looks like I send the majority of emails between 10pm and midnight, which makes sense because I mainly use Gmail for personal stuff in the evenings. The daily distribution of incoming mail is a lot flatter:
![]()

There’s a hint of a dip in the incoming mail around 6pm, where presumably people in my time zone are having their dinner. Then of course there’s a sharp drop after midnight when most people are asleep.
How many emails do I typically send in a day? I can find out by plotting the distribution of emails sent per day, with the number of emails sent per day on the x axis and the count on the y axis:
![]()

Here’s the raw data:
![{startdate, enddate} = Sort[sentdates][[{1, -1}]]; dailycount = Map[DatePlus[startdate, #] &, Range[0, DateDifference[startdate, enddate]]]; dailycount = {#, Count[sentdates, {Sequence @@ #[[;; 3]], __}]} & /@ dailycount; {startdate, enddate} = Sort[sentdates][[{1, -1}]]; dailycount = Map[DatePlus[startdate, #] &, Range[0, DateDifference[startdate, enddate]]]; dailycount = {#, Count[sentdates, {Sequence @@ #[[;; 3]], __}]} & /@ dailycount;](https://content.wolfram.com/sites/39/2012/04/Email-In24.png)
![]()
![]()
The distribution peaks sharply at zero, which means I most often send no emails in a day (from my Gmail account that is). I’m a low-frequency emailer apparently! The distribution of incoming mail per day is more interesting looking:
![]()

This looks like it could be a negative binomial distribution:
![{startdate, enddate} = Sort[incomingdates][[{1, -1}]]; dailycount = Map[DatePlus[startdate, #] &, Range[0, DateDifference[startdate, enddate]]]; dailycount = {#, Count[incomingdates, {Sequence @@ #[[;; 3]], __}]} & /@ dailycount; {startdate, enddate} = Sort[incomingdates][[{1, -1}]]; dailycount = Map[DatePlus[startdate, #] &, Range[0, DateDifference[startdate, enddate]]]; dailycount = {#, Count[incomingdates, {Sequence @@ #[[;; 3]], __}]} & /@ dailycount;](https://content.wolfram.com/sites/39/2012/04/Email-In29.png)
![]()

![]()
![]()
![fillcolor = RGBColor[0.9196002136263065`, 0.7993438620584421`, 0.19940489814602885`, 0.5`]; edgecolor = RGBColor[0.8442206454566262`, 0.5068284122987716`, 0.13566796368352788`]; fillcolor = RGBColor[0.9196002136263065`, 0.7993438620584421`, 0.19940489814602885`, 0.5`]; edgecolor = RGBColor[0.8442206454566262`, 0.5068284122987716`, 0.13566796368352788`];](https://content.wolfram.com/sites/39/2012/04/Email-In34.png)

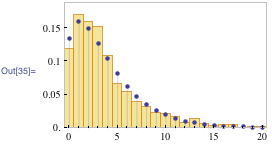
It’s fun to think about what this kind of distribution implies about the underlying process of receiving email. The standard interpretation of the negative binomial distribution NegativeBinomialDistribution[n,p] is the probability in a series of n + k trials that k failures happen before n successes occur, where the probability of success for each trial is p. It’s not immediately clear whether that’s a good model for the number of emails I receive in a day. What would the individual Bernoulli trials correspond to? (Actually, the fit is a little better to a beta negative binomial distribution, which allows the success probability p to vary over a beta distribution.)
We did all this analysis just using email time stamps! And it’s just the tip of the iceberg of what it’s possible to do with your email archive. You could import the email addresses on each email to see whom you email most often and how your most common recipients have changed over time. Or you could correlate sent mail to received mail to track message threads and plot things like thread length distribution or time delay in responding to emails. When you’re doing your analysis in Mathematica, the possibilities are endless.
You can find all the code I used in this post right here. Have fun!
Download this post as a Computable Document Format (CDF) file.


awesome…!!! after long time i saw such point to point article for analysis…. keep updating us…
thank you :)
What are the changes on code I have to do, to analyze my “HOTMAIL” mail?
Great start but I miss a more complicated view. What would be really cool is getting the email addresses,subjects for context (or data keyword analisys) , time stamps to plot the lifespan of subjects where emails where sent about and it’s growth with people getting involved.
great post!
I tried to do some of this using an MBOX file. but Mathematica said it was too large to read in to memory. Any tips for getting around this?
mailda = Import[“mail.mbox”, “Date”]
About how long did this take to run for some? I’ve been running for about 45 minutes now and still on the function
incomingdates = importemaildates[…]
my lengthsentdates is 6602 don’t know if that will help, email going back to 2005
Thanks
Wow, this is seriously cool. Thanks for sharing, though I’m sure I’m gonna be bombarding you with questions once I get around to try it out
Hi,
I seem to be having problems running this, for some reason import fail when using a mac.com email address (or me.com or icloud.com).
I suspect the reason could be because these servers require SSL authentication?
And I forgot the exception:
Java::excptn: A Java exception occurred: javax.mail.AuthenticationFailedException: Invalid credentials i51if17783740eeu.71
at com.sun.mail.imap.IMAPStore.protocolConnect(IMAPStore.java:566)
at javax.mail.Service.connect(Service.java:288)
at javax.mail.Service.connect(Service.java:169)
at InboxReader.dateStrings(InboxReader.java:13).
I tried this and found a bug in the code.
The PlotRange in dirunalplot in this code is:
PlotRange -> {{dates[[1, 1 ;; 2]], Automatic}, All}*)
This produced an error that I corrected by making the following change:
PlotRange -> {{dates[[1]], dates[[1 ;; 2]], Automatic}, All}
The code still works for Gmail with Mathematica 9 and the fix that was mentioned by David Srebnick in the comment above:
”
I tried this and found a bug in the code.
The PlotRange in dirunalplot in this code is:
PlotRange -> {{dates[[1, 1 ;; 2]], Automatic}, All}*)
This produced an error that I corrected by making the following change:
PlotRange -> {{dates[[1]], dates[[1 ;; 2]], Automatic}, All}
”
The code will not work in Mathematica 10 (you will see lines instead of dots, which will ruin the visualisation).
If you get a gmail login error, try disabling the additional security in your google account.
Recently I tried this code and it didn’t work, and I received an email from Google saying
Hi Farhat,
Someone just tried to sign in to your Google Account xxxxxxxxx@gmail.com from an app that doesn’t meet modern security standards.
Details:
xxxxxxxxxxxxxxxxxxxx (India Standard Time)
xxxx, xxx, India*
We strongly recommend that you use a secure app, like Gmail, to access your account. All apps made by Google meet these security standards. Using a less secure app, on the other hand, could leave your account vulnerable. Learn more.
Google stopped this sign-in attempt, but you should review your recently used devices:
Could this work with the new gmail security?
Awesome! Its in fact amazing piece of writing, I have got much
clear idea regarding from this piece of writing.
Hello there, You’ve done a fantastic job. I’ll definitely digg
it and personally recommend to my friends. I am sure they’ll be benefited from this site.
Hi there to all, the contents present at this site are genuinely
remarkable for people knowledge, well, keep up the good work fellows.
Thanks for finally writing about >Analyzing Your Email with
Mathematica-Wolfram Blog <Loved it!
My brother recommended I might like this blog. He was totally right.
This publish truly made my day. You can not believe simply
how a lot time I had spent for this info! Thank you!
For those who see lines instead of dots in “diurnalplot”, add “Joined -> False” at the end of the function definition.
Good post
Do you mind if I quote a few of your articles as long as
I provide credit and sources back to your site? My blog is in the very same area of interest as yours and my users would really benefit from
some of the information you present here. Please let me know
if this ok with you. Regards!
Feel free to cite this blog. However, do keep in mind that this post is now more than six years old.
Thanks, but it does not work for my yahoo account! Can you help us for the HOTMAIL accounts please?
Hi Feras,
It looks like Hotmail doesn’t support the IMAP protocol, so the code I wrote won’t work for a Hotmail account. To make it work for Hotmail you’d need to change the Java code to use the POP protocol.
Best,
Paul-Jean Letourneau
Hi Alberto,
Yes you can just use Mathematica’s Select function to select just the dates with reasonable years, before plotting them.
Take a look at the Select function and that should get you started.
Best regards,
Paul-Jean
Hi Vladislav,
did you manage to solve this problem? I am experiencing the same issue. Thanks in advance.