Today, I am happy to announce a free interactive course, Introduction to Partial Differential Equations, that will help students all over the world master this important subject. This course introduces partial differential equations (PDEs) from scratch and covers the most important types and their solution methods. It covers linear and nonlinear first-order PDEs; important cases of second-order PDEs, such as the heat, wave and Laplace equations; and a few famous PDEs, such as the Maxwell, Schrödinger, Navier–Stokes and Black–Scholes equations. The course is suitable for undergraduate students with exposure to multivariable calculus and ordinary differential equations (ODEs).

The study of PDEs is a vital and dynamic part of mathematics, with applications across physics, engineering and beyond. PDEs are used to describe many physical phenomena in fields such as fluid dynamics, electromagnetism, mechanics, classical optics and heat flow. Many fundamental laws of physics—including Maxwell’s equations, the Navier–Stokes equations, the heat equation, the wave equation and Schrödinger’s equation in quantum mechanics—are expressed in terms of PDEs.

Wolfram Language provides an ideal environment for studying this subject, thanks to its built-in computational capabilities, both symbolic and numerical, as well as its powerful visualization tools. It allows one to derive and manipulate PDEs symbolically, apply built-in functions for solving them analytically when possible and seamlessly switch to efficient numerical methods for more complex problems.

The course is designed to provide a user-friendly introduction to the theory and applications of PDEs, with interactive examples using Wolfram Language’s powerful built-in solving methods.

Clicking the following image, which links to the course, lets you explore its content:

Motivation from History

From the very beginning of modern science, many of the greatest advances in physics, engineering and mathematics have come through the study of PDEs. Isaac Newton and Gottfried Leibniz introduced calculus to describe motion and change. Soon after, PDEs emerged as the natural language for expressing the laws of nature. For example, Daniel Bernoulli used them to model vibrating strings, Joseph Fourier applied them to heat conduction and Claude-Louis Navier and George Stokes developed equations for fluid flow. These historical milestones show that PDEs were not abstract inventions, but powerful tools created to solve real problems. Studying PDEs today continues this tradition, equipping us with the same mathematical framework that shaped centuries of scientific progress.

Overview

Students taking the course will receive an introduction to PDEs starting from their basic definitions, properties and characteristics, and solving methods. They will also study some well-known second-order PDEs, including the heat, wave and Laplace equations. Finally, four famous PDEs—the Black–Scholes, Schrödinger, Maxwell and Navier–Stokes equations—will be discussed.

The course framework can be viewed in the following:

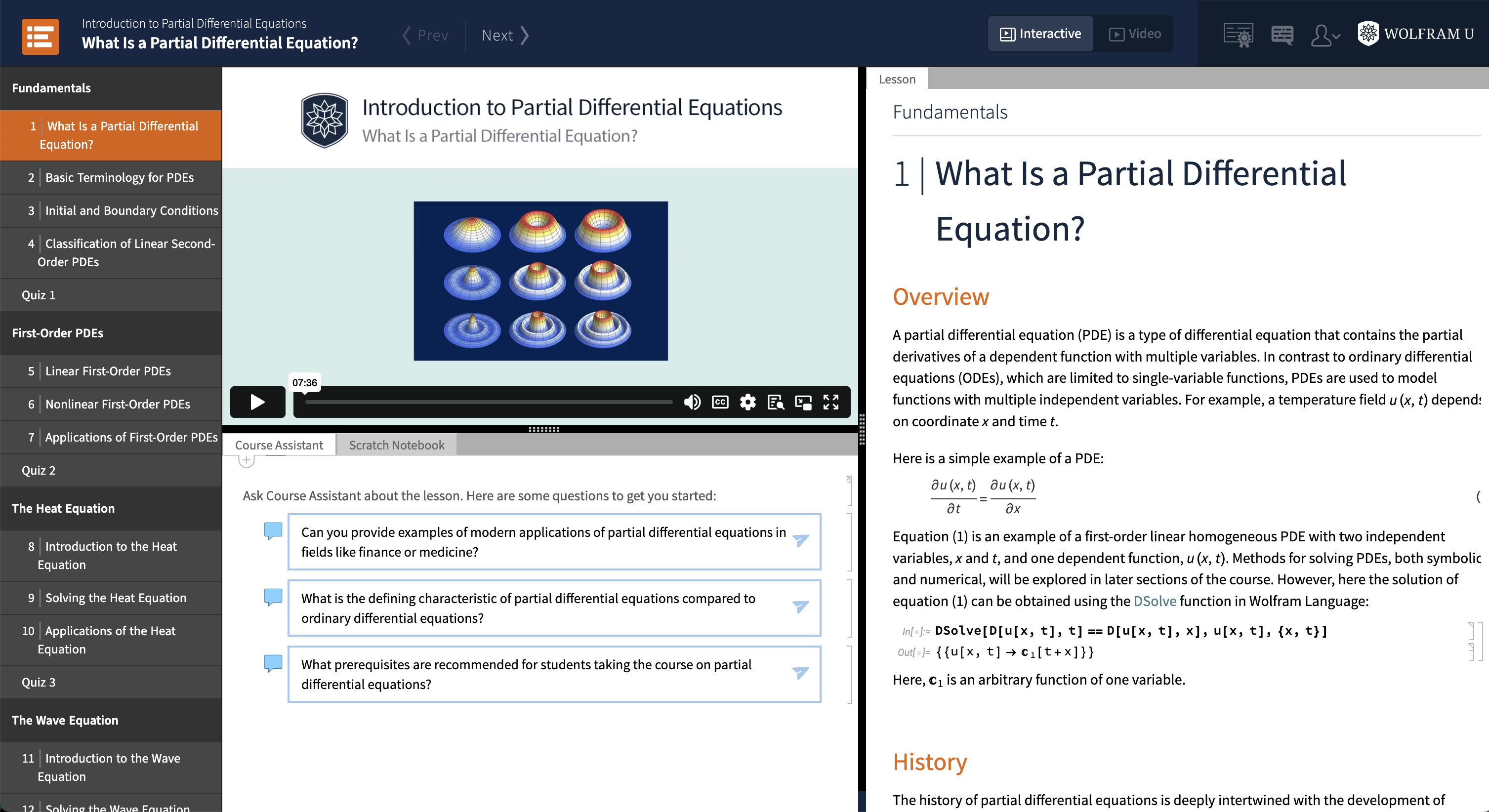
The course consists of lessons, exercises and quizzes designed to help you master all the fundamentals of this subject. Students who want to review prerequisite topics can find them in the related Wolfram U interactive courses Introduction to Multivariable Calculus and Introduction to Differential Equations.

Let’s see in more detail what the course looks like.

Lessons

The course is organized into 24 lessons. Each lesson consists of a video and its written transcript.

The first lesson, “What Is a Partial Differential Equation?,” is a historical introduction to the topic, which shows the importance and modern applications of PDEs.

Later lessons describe various types of PDEs and their solving methods. All lessons contain numerous solved examples, often illustrating the use of Wolfram Language code and functionality for solving PDEs and for the visualization of obtained solutions.

Lesson videos range from 7 to 15 minutes in length and are accompanied by a transcript notebook. These notebooks can either be downloaded or viewed in the browser. Students can experiment with them and try the examples in a scratch notebook directly in the browser on the same webpage as the video. Users who subscribe to Wolfram Notebook Assistant + LLM Kit have access to the AI Course Assistant to get extra help with questions and coding examples to further explore the concepts in the course.

Exercises

Each lesson contains three to six exercises that review the material covered in the lesson. The solutions are provided, most of the time in the form of Wolfram Language code. Exercises are a key component of the learning experience, as they enhance the material covered in each lesson.

For example, following is an exercise from Lesson 11:

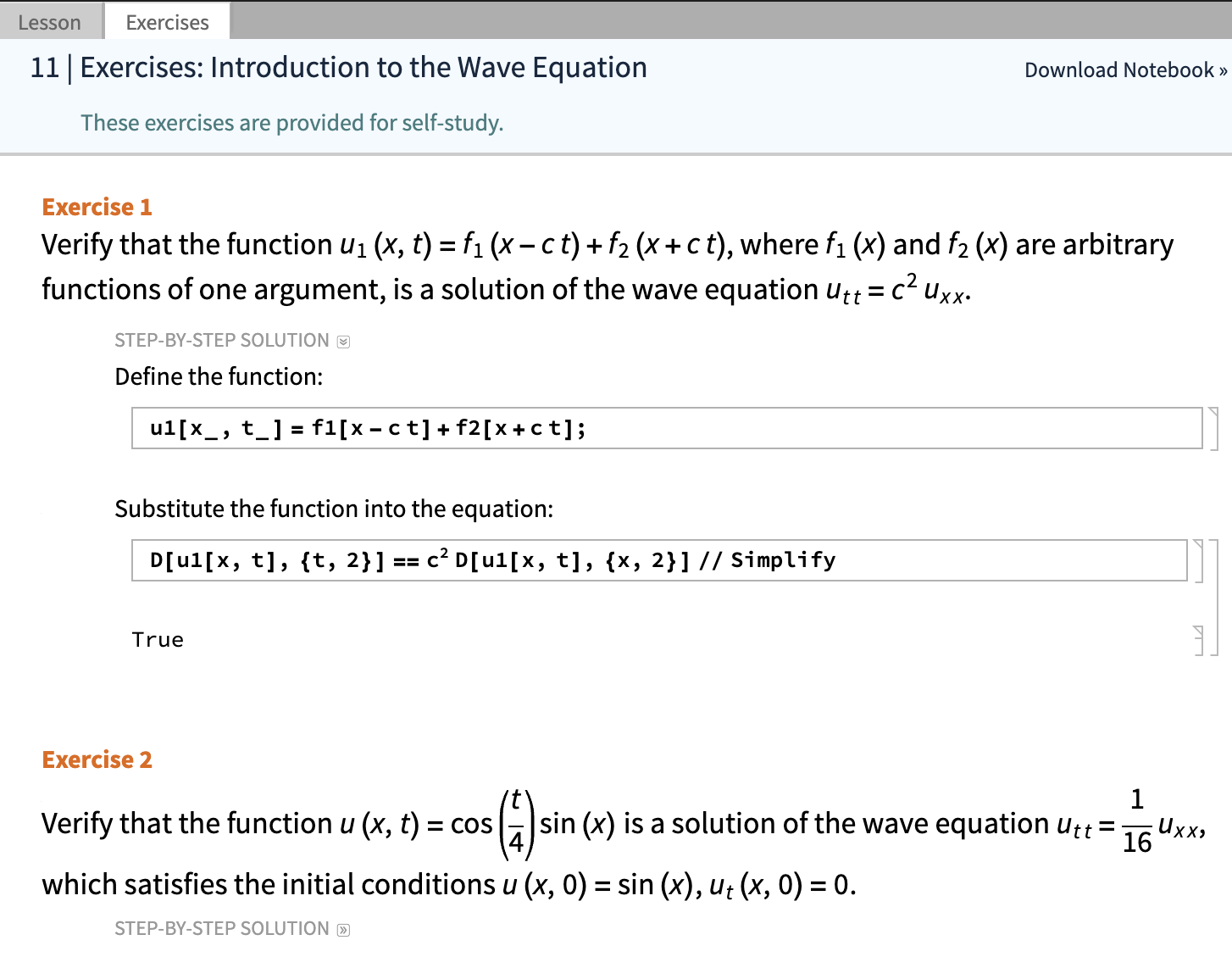
Students can experiment with Wolfram Language notebooks and try variations of the exercises or adapt the code to their own explorations.

Quizzes

The 24 lessons of the course are grouped into seven sections. Each section ends with a quiz with several multiple-choice questions and one free-response question reviewing the material contained in the section. The quiz is intended to help students with questions that are similar to the exercises and provide feedback on answers:

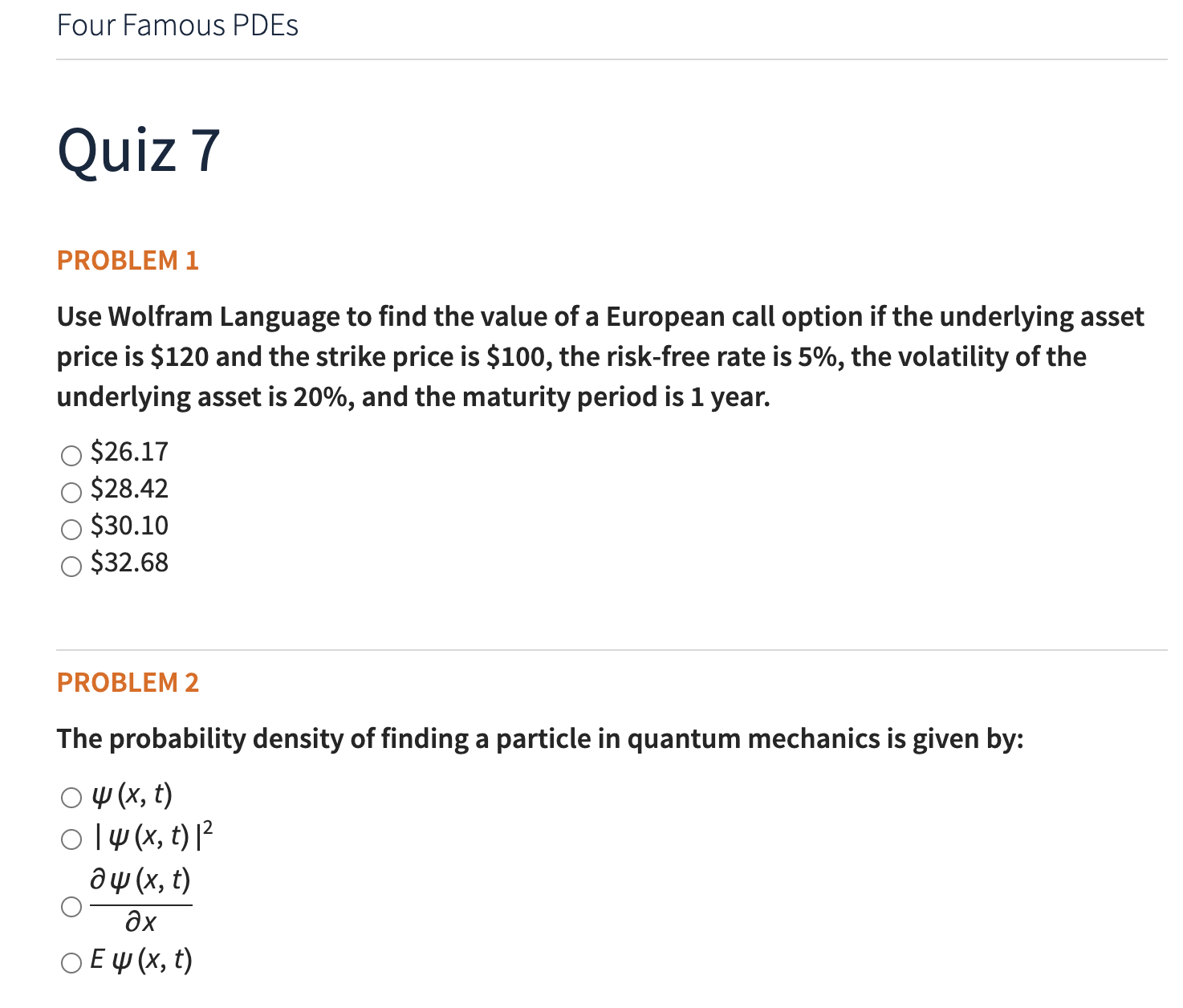
Students are encouraged to use any method to solve the quiz problems, whether by hand or using Wolfram Language. A scratch notebook is provided for that purpose on the right-hand side of the quiz webpages.

Course Review

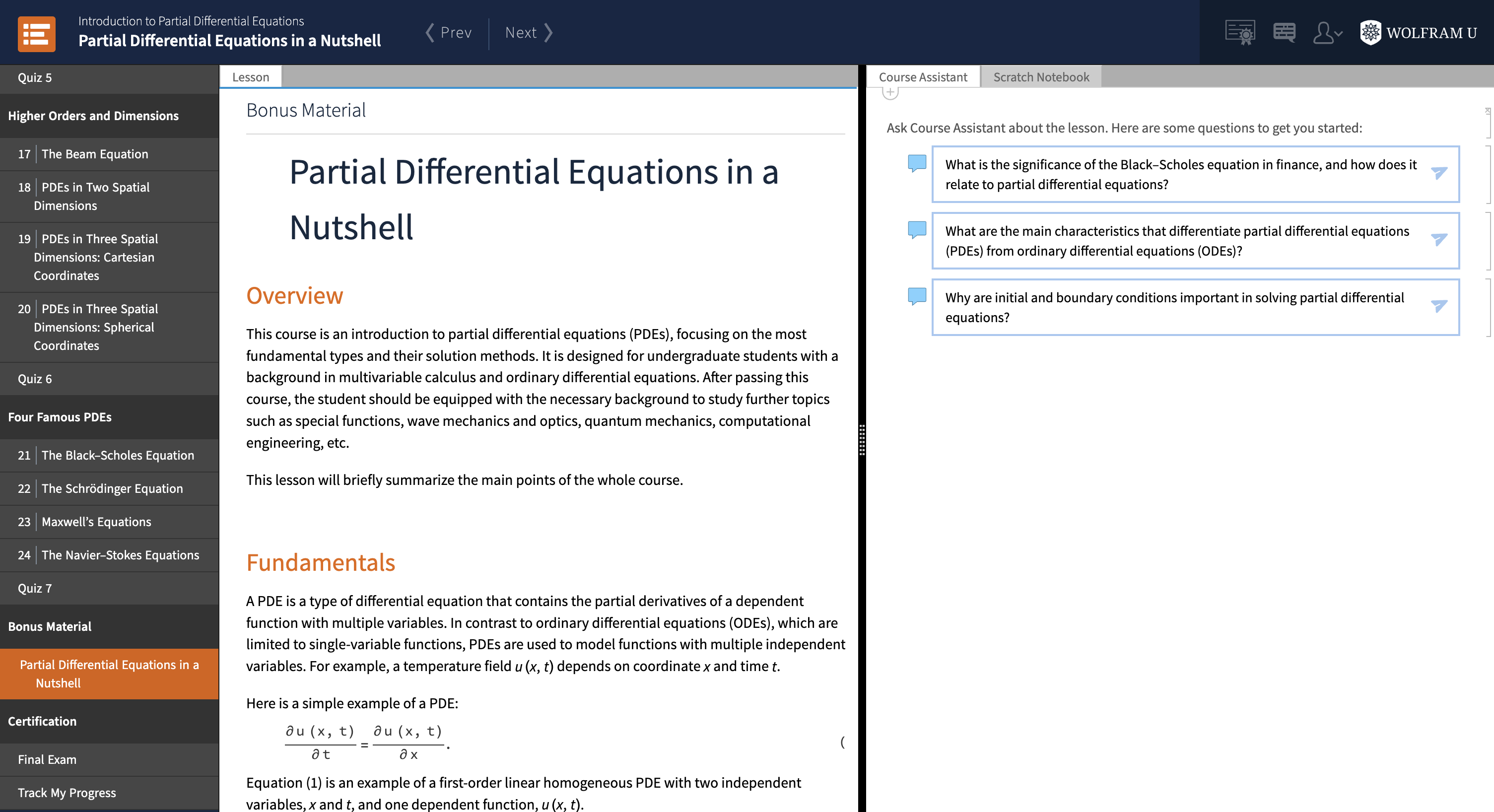
Studying a subject like PDEs can be challenging because it requires learning many new concepts and theories within a short time. To support your review of the material, the course ends with a final summary lesson titled “Partial Differential Equations in a Nutshell”:

Course Certificate

Students who finish the course and pass all the quizzes can get a certificate of completion.

A final exam is also available at the end of the course. Passing it entitles the student to a Level 1 certification for proficiency in PDEs. It’s easy to track which videos you’ve completed and the status of your quizzes and exam by using the “Track My Progress” section of the course. Your shareable certificates are automatically generated and immediately available to you upon completing the requirements.

A Building Block for Success

A thorough understanding of PDEs is highly desirable for students not only in mathematics but also in physics and engineering. This course aims to help students master the basics of partial differential equations and to provide a solid foundation for their further studies.

Acknowledgements

I would like to sincerely thank Devendra Kapadia, Anisha Basil, Joyce Tracewell, Tigran Ishkhanyan, Roger Germundsson, Cassidy Hinkle, Jamie Peterson, Roberto Martinez, Naoko Glowicki, Ryan Domier, Adam Bramowicz, Mariel Laugesen, Laura Millar, Laura Crawford, Jay Warendorff, Paige Vigliarolo, Tim Shedelbower and Bailey Long for their work on various aspects of the course.

Finally, I would like to mention the excellent tutorial on symbolic PDEs by Unal Goktas, which provided the starting point for this course.