Today, I am excited to announce a free interactive course, Introduction to Special Functions, to help students worldwide master this fascinating subject. To the best of our knowledge, this is the first course ever to offer such comprehensive coverage of concepts and groups of special functions.

Special functions are a class of mathematical functions that arise when solving differential equations, summing series and calculating integrals. They originated in the eighteenth century, when mathematicians studying problems in physics, engineering and mathematics sought to describe increasingly complex scientific phenomena. Special functions are more general than the well-known elementary ones that every high-school student is familiar with.

Wolfram Language offers a uniquely powerful environment for studying both the theory and applications of special functions, combining symbolic and numerical computation with rich visualization tools. Special functions have been part of the system since Version 1.0 in 1988, and today nearly all functions found in the mathematical literature are implemented. This course highlights 100 of the most fundamental special functions from the collection of 300 mathematical functions available in Wolfram Language, providing a foundation for exploring these functions in greater depth and uncovering new insights and applications.

The course is designed to provide a user-friendly introduction to the theory of special functions, with interactive examples using Wolfram Language’s powerful built-in methods. These include working with special functions, solving differential equations, calculating integrals and derivatives, generating series expansions and more. Every built-in function mentioned in the course has a reference page in the Wolfram Language & System Documentation Center. These pages contain a rich collection of examples illustrating properties and applications, which can be used alongside the course to deepen understanding of special functions.

The course is intended for STEM majors, teachers and professors seeking new ways to present special functions and anyone interested in learning about special functions and their implementation in Wolfram Language.

Clicking the following image, which links to the course, lets you explore its content.

History and Motivation

Gamma, Bessel and hypergeometric functions, Legendre polynomials and others were systematically studied and cataloged, primarily because they were used to solve equations such as Laplace’s and the wave equation. Their development was closely tied to advances in mathematical physics, particularly in electromagnetism, fluid dynamics and quantum mechanics. Euler, Riemann, Gauss, Jacobi and many other distinguished scientists contributed to the theory of special functions.

The list of special functions is extensive, but studying them is important for many reasons across theoretical mathematics, applied sciences and engineering. These functions often arise as solutions to differential equations that model physical systems, so understanding them provides deeper insight into both the properties of these equations and the nature of solutions in real-world applications. Many special functions have well-established properties—such as orthogonality, recurrence relations and integral representations—that make them valuable tools for simplifying and solving problems. Their series expansions are extremely useful for approximation and computation, allowing for precise and efficient numerical work in engineering and scientific applications. Special functions also appear in modern fields, including quantum mechanics, electromagnetism, statistical mechanics and mathematical biology, enabling researchers to tackle problems across diverse disciplines. Overall, they serve as a cornerstone of both pure and applied mathematics, bridging theory and practical application, and are not merely historical curiosities. The theory of special functions is actively evolving, with new generalizations, extensions and applications being developed nearly every day, making it a vibrant and continuously advancing area of study.

Overview

This course includes five hours of video lessons to fully cover concepts and groups of special functions. Students taking the course will receive an introduction to the theory of special functions, beginning with fundamental topics from calculus, visualization, numerical methods and complex analysis. The course then explores ordinary differential equations (viewed both as data structures and as generators of special functions) before moving into specific groups of functions: gamma and related functions; special integrals; orthogonal polynomials; Bessel and related functions; Airy functions; hypergeometric functions; elliptic functions and integrals; zeta functions; Mathieu, spheroidal, Lamé and Heun classes of functions; multivariate hypergeometric functions; and finally, Meijer’s G- and Fox’s H-functions.

The final section provides a summary of the course in a printable 60-page booklet format that covers all of the above groups of special functions and can also serve as a standalone short interactive textbook. More about this final section later in the blog post!

The course framework can be viewed in the following image:

The course consists of lessons, exercises, quizzes and a final exam designed to help you master and demonstrate your proficiency in this subject.

Necessary mathematical prerequisites for the course are exposure to single-variable calculus, differential equations and complex analysis.

Let’s see in more detail what the course looks like.

Lessons

The course is organized into 29 lessons. Each lesson includes a video and a written transcript. Let’s take a closer look at the first section of the course, which serves as an introduction to the subject.

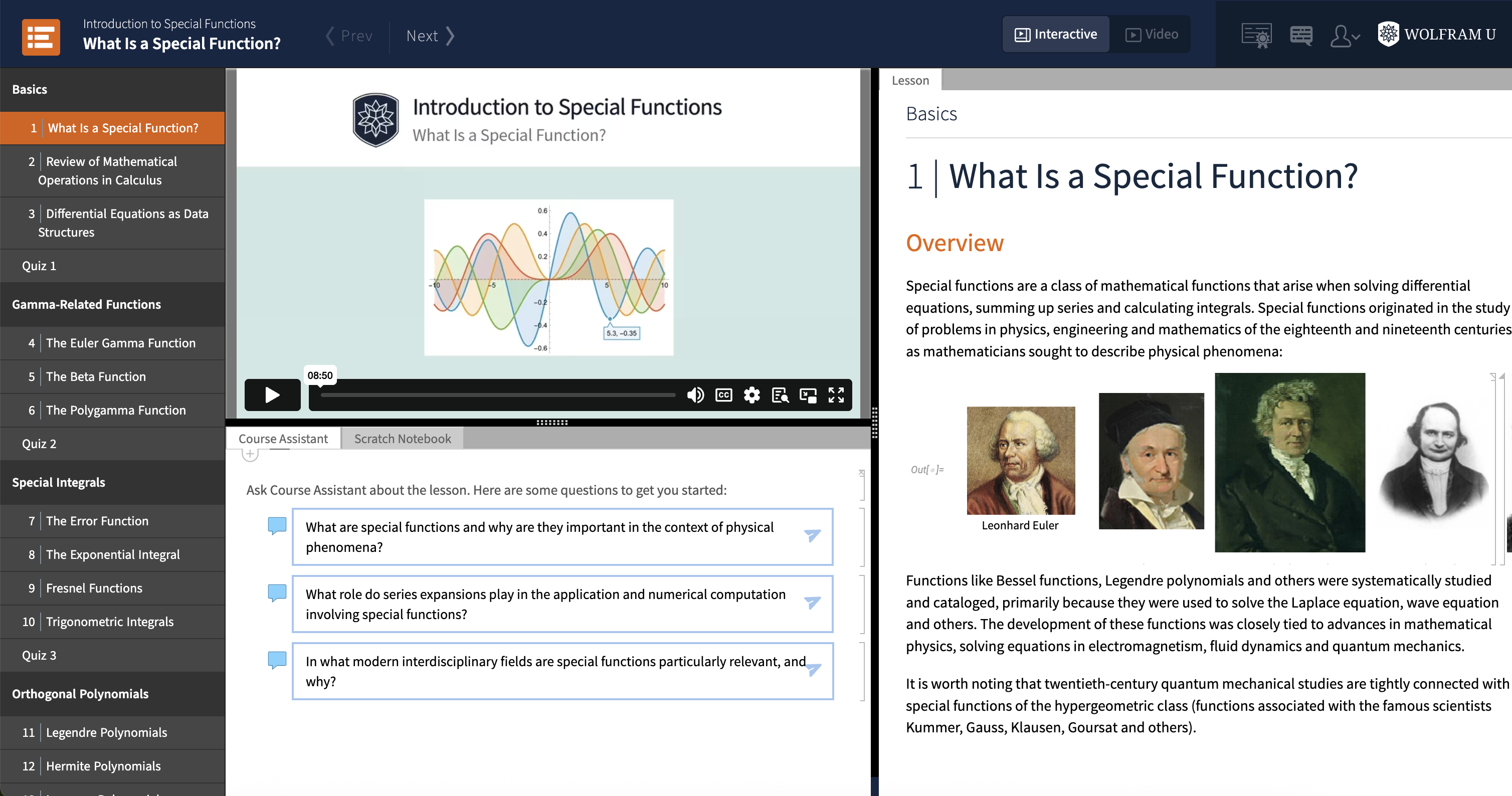
The first lesson—“What Is a Special Function?”—is an introduction to the topic and demonstrates the transition from elementary to special functions. It also discusses the motivation for studying special functions and provides a brief review of the literature.

The second lesson, “Review of Mathematical Operations in Calculus,” showcases common operations applied to special functions, making extensive use of Wolfram Language’s built-in functionality. The final introductory lesson, “Differential Equations as Data Structures,” presents ODEs from a new perspective—as cornerstones of the theory of special functions.

All lessons feature numerous solved examples, frequently illustrating how Wolfram Language functionality can be applied to different special functions.

Lesson videos are 7–19 minutes in length and are accompanied by transcript notebooks. These notebooks can be viewed in the browser or downloaded, allowing students to experiment with the examples directly in a scratch notebook on the same webpage as the video. Students who subscribe to Wolfram Notebook Assistant + LLM Kit have access to the AI Course Assistant for getting extra help with questions and coding examples to further explore the concepts in the course.

Exercises

Each lesson contains five or more exercises that review the material covered. Solutions are provided—most often in the form of Wolfram Language code—along with explanations and mathematical derivations. Exercises are a key part of the learning experience, as they reinforce and expand upon the concepts presented in each lesson. Some exercise sets include advanced problems to provide students with a deeper theoretical understanding of the topic. These advanced exercises often dive further into the theory and explore subjects not covered in the videos or notebooks.

For example, the following is an exercise from Lesson 4.

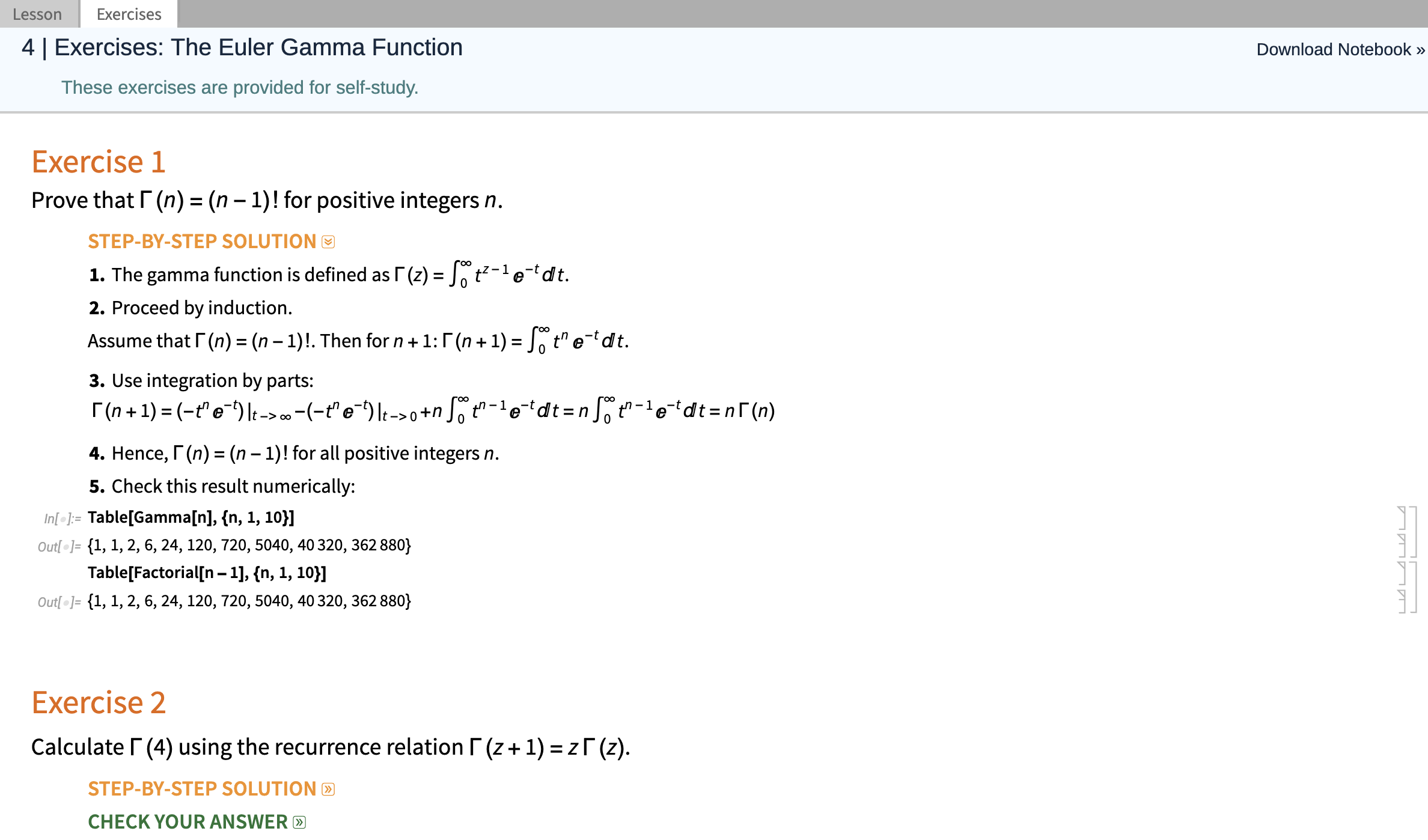
Students can experiment with Wolfram Language notebooks and try variations of the exercises or adapt the code to their own explorations.

Quizzes

The 29 course lessons are organized into nine sections. Each section concludes with a quiz containing multiple-choice and free-response questions that review the material covered. The difficulty level is sometimes lower than that of the lesson exercises because the quizzes are designed primarily to help students reinforce the key points of each section.

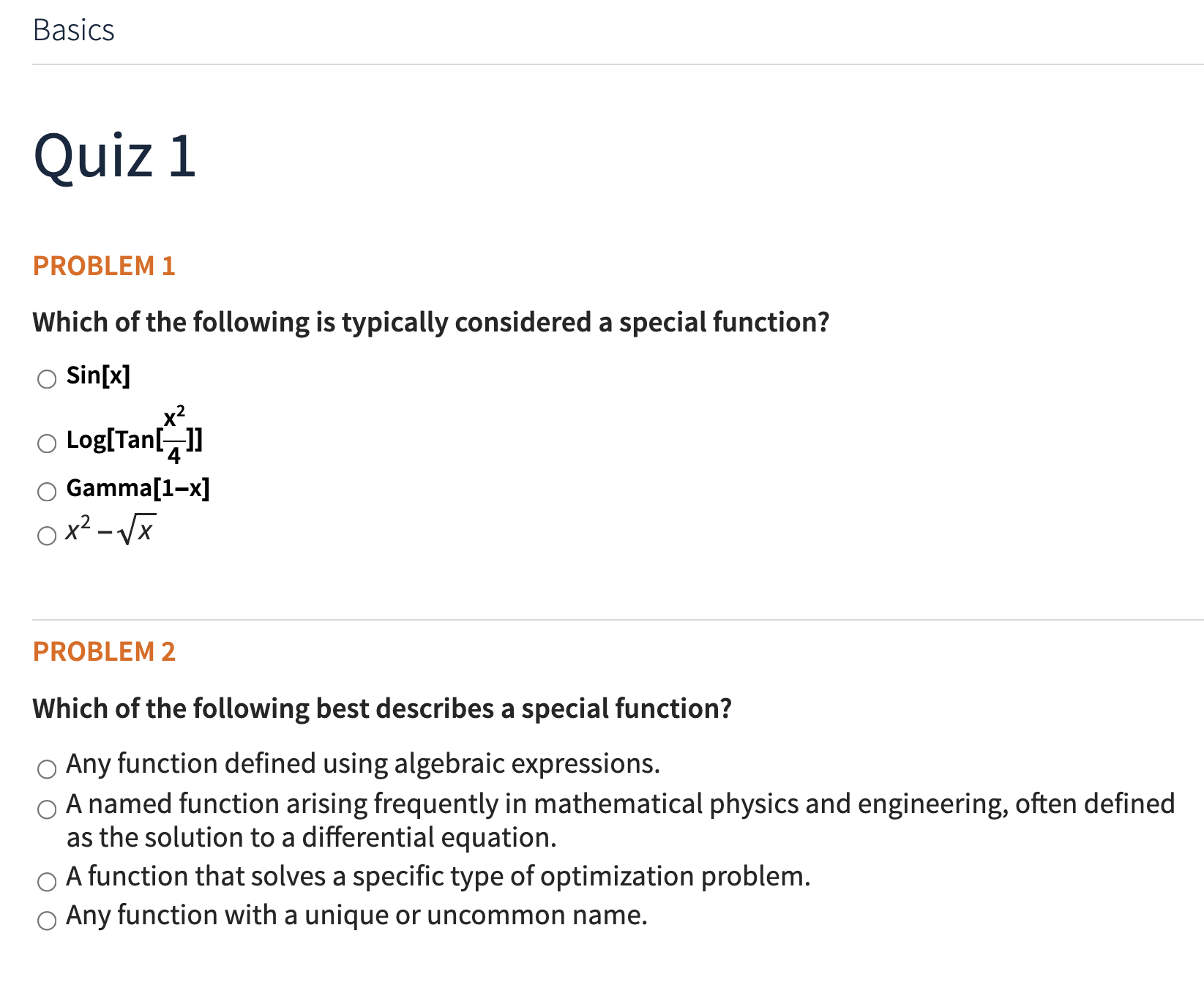
The quizzes provide immediate feedback on the correctness of answers.

Students are encouraged to use any method to solve the quiz problems—whether by hand or with Wolfram Language. For convenience, a scratch notebook is available on the bottom of each quiz webpage.

Course Review

One of the challenges in studying special functions is that the subject is both advanced and rarely taught in a systematic way at universities. It requires mastering a wide range of new concepts and approaches in a relatively short time. Bringing all of these ideas together in one place has traditionally been difficult.

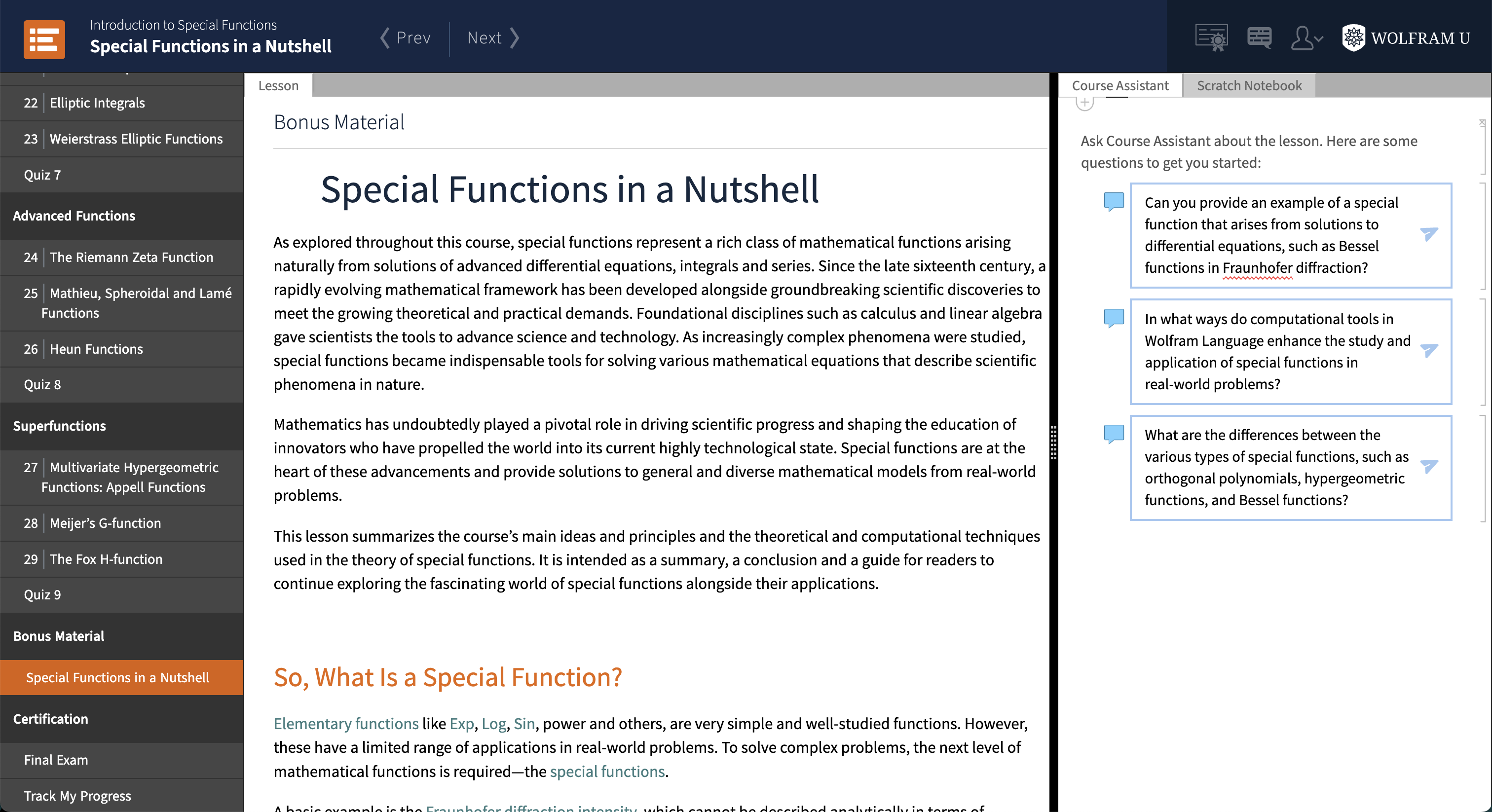
To address this, the course concludes with a special review lesson, “Special Functions in a Nutshell.” This bonus material serves as a concise, ready-to-use interactive handbook that brings together the main groups of special functions. It is designed to help students review and connect the material, providing a unique resource that opens up enormous potential for further study and applications.

Course Certificate

Students who finish the course and pass all the quizzes earn a certificate of completion:

Passing the final exam entitles the student to a Level 1 certification for proficiency in special functions. It’s easy to track which videos you’ve completed and the status of your quizzes and exam by using the “Track My Progress” section of the course. Your shareable certificates are automatically generated and immediately available to you upon completing the requirements.

Acknowledgements

I would like to sincerely thank Devendra Kapadia, Anisha Basil, Aram Manaselyan, Paul Abbott, Anush Sargsyan, Joyce Tracewell, Cassidy Hinkle, Jamie Peterson, Adam Bramowicz, Bob Owens, Ryan Domier, Tim Shedelbower, Avery Ewing, Roberto Martinez, Arben Kalziqi, Laura Millar and Mariel Laugesen for their work on various aspects of the course, including valuable and insightful discussions in shaping the material. I am also deeply grateful to my family for their unwavering support and patience throughout the development of this course.

Finally, I would like to express my sincere gratitude to all the researchers and developers who have contributed to the special functions project in Wolfram Language over the past four decades—among them Stephen Wolfram, Jerry Keiper, Roger Germundsson, Oleg Marichev, Michael Trott, Victor Adamchik, Daniel Lichtblau, Sasha Pavlyk, Bhuvanesh Bhatt, Jan Mangaldan and many others. Their work has made this field what it is today, and I am truly thankful for their dedication and inspiration.