In our daily lives, individuals, corporations and societies are constantly involved in making decisions. We hope to make optimal choices, especially when faced with recurrent decision processes. Thus we care about why and how our decision processes change over time. As a practicing engineer and an instructor in higher education, it is my opinion that a course on how optimal decisions are made and change should be part of a standard curriculum for a wide range of fields, including engineering, business, economics, project management and social sciences.

Wolfram Language provides powerful tools to compute and visualize both the optimal behaviors of decisions using game theory and an extension to a new field theory of games that explores how decisions change in time. I am excited to announce a free interactive course on decision process theory that will help students from all over the world explore this subject.

The course begins with a basic introduction to game theory and extends that theory to focus on how decisions change in time. A Wolfram Language toolkit for decision process theory (DPT) is provided in the course to facilitate a basic understanding of decision processes and provides ways to visualize them. Using the toolkit, examples and hands-on exercises are emphasized in lieu of detailed theoretical discussions. The level of the course is suitable for students with no prior knowledge of game theory.

Clicking the image below, which links to the course, lets you explore its content.

Motivation from History

The ideas discussed in this course go back to the notion of utility introduced by the Swiss mathematician and physicist Daniel Bernoulli (1700–1782), who is also known for his contributions to fluid dynamics. The ideas were incorporated into a theory of decision making explained in the book Theory of Games and Economic Behavior by the mathematician John von Neumann (1903–1957) and the economist Oskar Morgenstern (1902–1977). Von Neumann and Morgenstern showed how to put decision processes into a normal form and, using the analogy of zero-sum recreational games, compute optimal behaviors for zero-sum decision processes. These ideas were extended by the mathematician John Nash (1928–2015) to non-zero-sum games.

I took these ideas and extended them to a field theory of games using the mathematics of differential geometry and based on utilities to consider how games behave in time: a decision process theory whose behaviors are very similar to fluids. More recently, I used Wolfram Language to create a toolkit approach to decision process theory, on which this course is based.

Overview

Students taking this course will receive an introduction to classical game theory and use a curated set of Wolfram Language functions to compute the optimal behavior of games. Based on examples, the concepts of strategic thinking are applied to classic examples of games, such as the Prisoner’s Dilemma. The student will get a working knowledge of how to use decision process theory tools. A scratch notebook and the new Wolfram U Course Assistant, powered by Wolfram LLM Kit, are available for the student to use for their own decision examples to further explore the ideas presented in the course.

The course framework can be viewed in the following image.

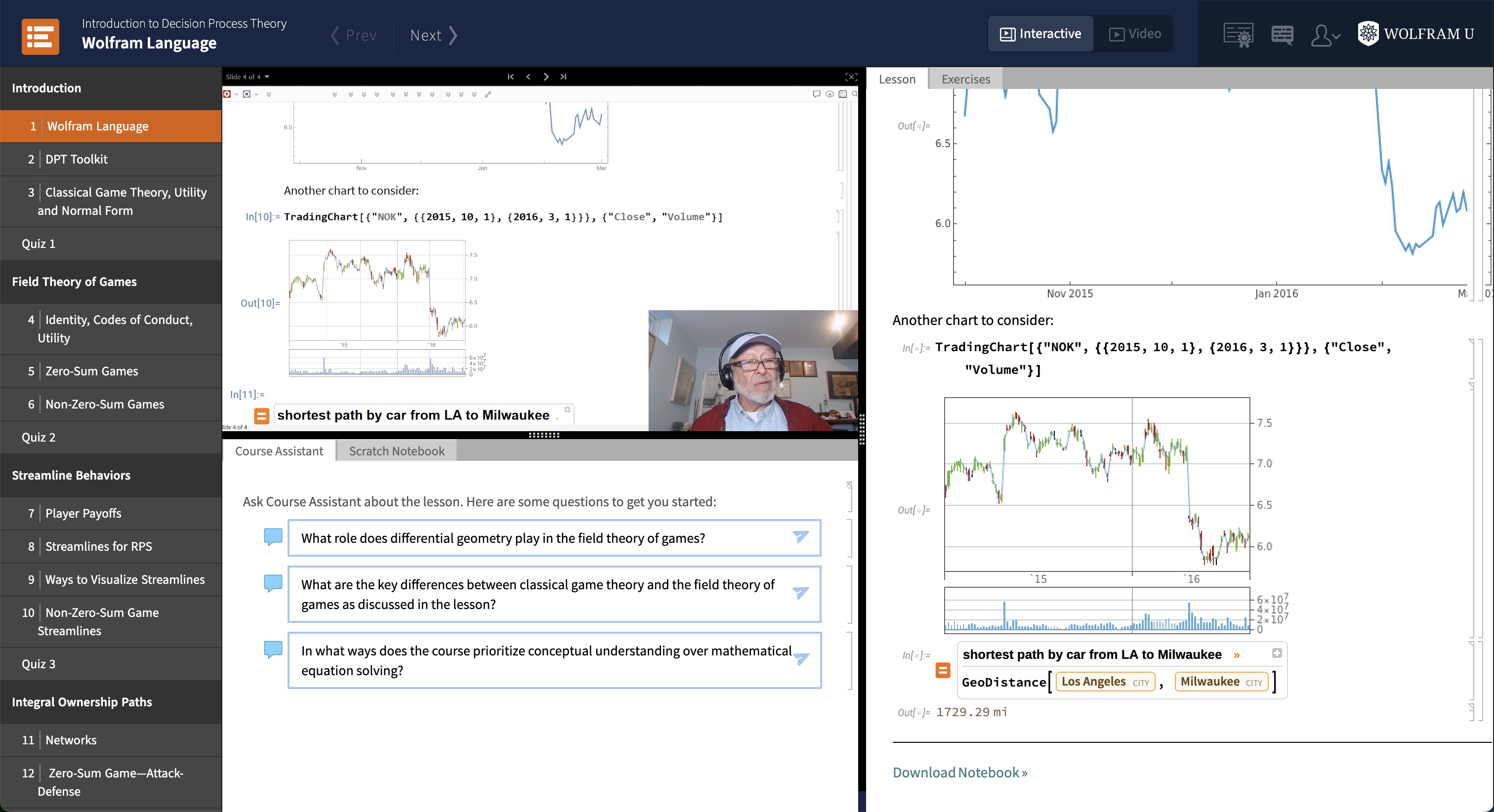
The course consists of lessons, exercises, quizzes and a final exam designed to help you master all the fundamentals of this subject. As you work through the course, ask Course Assistant anything about a lesson and it will provide you with contextually aware answers and even relevant code you can try. While access to the course content is free, Course Assistant requires a subscription to Wolfram Notebook Assistant + LLM Kit. Necessary mathematical prerequisites for the course are exposure to single-variable and multivariable calculus.

Let’s see in more detail what the course looks like.

Lessons

The course is organized into 38 lessons. Each lesson consists of a video lecture and its written transcript. Along with the video, each lesson is also covered by a book chapter that expands the discussion further, at times providing background material and references not discussed in the video.

The first lesson, “Wolfram Language,” introduces the course with emphasis on how Wolfram Language will be used based on the DPT Toolkit. The second lesson, “DPT Toolkit,” introduces the toolkit.

Later lessons expand on these ideas to zero-sum and non-zero-sum games, both using game theory and the time-dependent field theory of games. The lessons include numerous solved examples illustrated using the functionality of Wolfram Language both to compute and visualize the results.

Lesson videos range from 5–12 minutes in length. The accompanying lesson notebooks can either be downloaded or viewed in the browser. Students are encouraged to experiment with them. A scratch notebook is provided in the course framework, which can be useful during the course and thereafter.

Exercises

Each lesson contains exercises that review the material covered in the lesson, as well as expand the content of the lesson. The solutions are provided, sometimes in the form of Wolfram Language.

For example, here are two exercises from lesson 30.

Students can experiment with Wolfram Language notebooks and try variations of the exercises or adapt the code to their own explorations.

Quizzes

The 38 lessons of the course are grouped into 10 sections. Each section ends with a quiz with multiple-choice problems reviewing the material contained in the section. The level of difficulty is roughly the same as that of the lesson exercises; the quiz is intended to help students with reviewing the main points of the section.

The quiz provides feedback about the correctness of the answers.

Students can use any method to solve some of the quiz problems; some require the DPT Toolkit and/or Wolfram Language. The scratch notebook is provided for that purpose and appears on the right-hand side of the screen along with each quiz.

Course Certificate

Students who finish the course and pass all the quizzes will earn a certificate of completion.

A final exam is also available at the end of the course. Passing it entitles the student to Level 1 certification for proficiency in decision process theory. It’s easy to track which videos you’ve completed and the status of your quizzes and exam by using the “Track My Progress” section of the course. Your shareable certificates are automatically generated and immediately available to you upon completing the requirements.

A Building Block for Success

I believe all of us hope to make optimal choices and to gain understanding as our decision processes change over time. I am pleased to have put together a course to help us compute quickly not only optimal choices, but how even non-optimal choices change over time. Using foundational concepts of game theory, this course aims to help students become proficient in expanding these ideas further.

Acknowledgments

I would like to thank Anisha Basil, Joyce Tracewell, Cassidy Hinkle, Bob Owens, Adam Bramowicz, John McNally, Marc Vicuna, Laura Crawford, Mariel Laugesen, Naoko Glowicki, Paige Vigliarolo and Bailey Long for their work on various aspects of the course.