Two years ago we released Version 13.0 of Wolfram Language. Here are the updates in compiler and evaluation since then, including the latest features in 14.0. The contents of this post are compiled from Stephen Wolfram’s Release Announcements for 13.1, 13.2, 13.3 and 14.0.

The Great Integration Story: Integrating External Code (January 2024)

It’s been possible to call external code from Wolfram Language ever since Version 1.0. But in Version 14 there are important advances in the extent and ease with which external code can be integrated. The overall goal is to be able to use all the power and coherence of the Wolfram Language even when some part of a computation is done in external code. And in Version 14 we’ve done a lot to streamline and automate the process by which external code can be integrated into the language.

Once something is integrated into the Wolfram Language it just becomes, for example, a function that can be used just like any other Wolfram Language function. But what’s underneath is necessarily quite different for different kinds of external code. There’s one setup for interpreted languages like Python. There’s another for C-like compiled languages and dynamic libraries. (And then there are others for external processes, APIs, and what amount to “importable code specifications”, say for neural networks.)

Let’s start with Python. We’ve had ExternalEvaluate for evaluating Python code since 2018. But when you actually come to use Python there are all these dependencies and libraries to deal with. And, yes, that’s one of the places where the incredible advantages of the Wolfram Language and its coherent design are painfully evident. But in Version 14.0 we now have a way to encapsulate all that Python complexity, so that we can deliver Python functionality within Wolfram Language, hiding all the messiness of Python dependencies, and even the versioning of Python itself.

As an example, let’s say we want to make a Wolfram Language function Emojize that uses the Python function emojize within the emoji Python library. Here’s how we can do that:

And now you can just call Emojize in the Wolfram Language and—under the hood—it’ll run Python code:

The way this works is that the first time you call Emojize, a Python environment with all the right features is created, then is cached for subsequent uses. And what’s important is that the Wolfram Language specification of Emojize is completely system independent (or as system independent as it can be, given vicissitudes of Python implementations). So that means that you can, for example, deploy Emojize in the Wolfram Function Repository just like you would deploy something written purely in Wolfram Language.

There’s very different engineering involved in calling C-compatible functions in dynamic libraries. But in Version 13.3 we also made this very streamlined using the function ForeignFunctionLoad. There’s all sorts of complexity associated with converting to and from native C data types, managing memory for data structures, etc. But we’ve now got very clean ways to do this in Wolfram Language.

As an example, here’s how one sets up a “foreign function” call to a function RAND_bytes in the OpenSSL library:

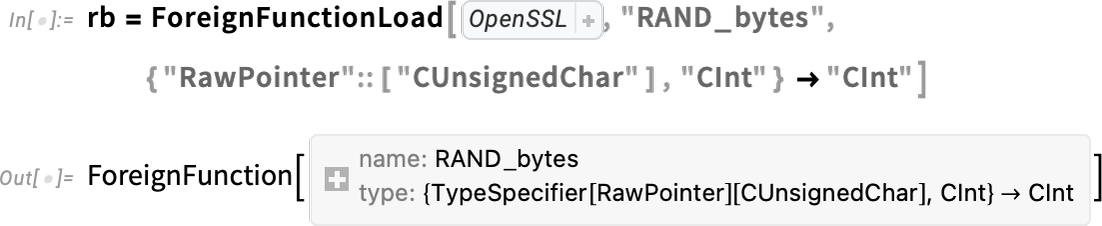
Inside this, we’re using Wolfram Language compiler technology to specify the native C types that will be used in the foreign function. But now we can package this all up into a Wolfram Language function:

And we can call this function just like any other Wolfram Language function:

Internally, all sorts of complicated things are going on. For example, we’re allocating a raw memory buffer that’s then getting fed to our C function. But when we do that memory allocation we’re creating a symbolic structure that defines it as a “managed object”:

And now when this object is no longer being used, the memory associated with it will be automatically freed.

And, yes, with both Python and C there’s quite a bit of complexity underneath. But the good news is that in Version 14 we’ve basically been able to automate handling it. And the result is that what gets exposed is pure, simple Wolfram Language.

But there’s another big piece to this. Within particular Python or C libraries there are often elaborate definitions of data structures that are specific to that library. And so to use these libraries one has to dive into all the—potentially idiosyncratic—complexities of those definitions. But in the Wolfram Language we have consistent symbolic representations for things, whether they’re images, or dates or types of chemicals. When you first hook up an external library you have to map its data structures to these. But once that’s done, anyone can use what’s been built, and seamlessly integrate with other things they’re doing, perhaps even calling other external code. In effect what’s happening is that one’s leveraging the whole design framework of the Wolfram Language, and applying that even when one’s using underlying implementations that aren’t based on the Wolfram Language.

Super-Efficient Compiler-Based External Code Interaction (June 2022)

Let’s say you’ve got external code that’s in a compiled C-compatible dynamic library. An important new capability in Version 13.1 is a super-efficient and very streamlined way to call any function in a dynamic library directly from within the Wolfram Language.

It’s one of the accelerating stream of developments that are being made possible by the large-scale infrastructure build-out that we’ve been doing in connection with the new Wolfram Language compiler—and in particular it often leverages our sophisticated new type-handling capabilities.

As a first example, let’s consider the RAND_bytes (“cryptographically secure pseudorandom number generator”) function in OpenSSL. The C declaration for this function is:

In Version 13.1 we now have a symbolic way to represent such a declaration directly in the Wolfram Language:

&#10005

(In general we’d also have to specify the library that this function is coming from. OpenSSL happens to be a library that’s loaded by default with the Wolfram Language so you don’t need to mention it.)

There are quite a few new things going on in the declaration. First, as part of our collection of compiled types, we’re adding ones like "CInt" and "CChar" that refer to raw C language types (here int and char). There’s also CArray which is for declaring C arrays. Notice the new ::[ ... ] syntax for TypeSpecifier that allows compact specifications for parametrized types, like the char* here, that is described in Wolfram Language as "CArray"::["CChar"].

Having set up the declaration, we now need to create an actual function that can take an argument from Wolfram Language, convert it to something suitable for the library function, then call the library function, and convert the result back to Wolfram Language form. Here’s a way to do that in this case:

&#10005

What we get back is a compiled code function that we can directly use, and that works by very efficiently calling the library function:

&#10005

The FunctionCompile above uses several constructs that are new in Version 13.1. What it fundamentally does is to take a Wolfram Language integer (which it assumes to be a machine integer), cast it into a C integer, then pass this to the library function, along with a specification of a C char * into which the library function will put its result, and from which the final Wolfram Language result will be retrieved.

It’s worth emphasizing that most of the complexity here has to do with handling data types and conversions between them—something that the Wolfram Language goes to a lot of trouble to avoid usually exposing the user to. But when we’re connecting to external languages that make fundamental use of types, there’s no choice but to deal with them, and the complexity they involve.

In the FunctionCompile above the first new construct we encounter is

&#10005

The basic purpose of this is to create the buffer into which the external function will write its results. The buffer is an array of bytes, declared in C as char *, or here as "CArray"::["CChar"]. There’s an actual wrinkle though: who’s going to manage the memory associated with this array? The "Managed":: type specifier says that the Wolfram Language wrapper will do memory management for this object.

The next new construct we see in the FunctionCompile is

&#10005

Cast is one of a family of new functions that can appear in compilable code, but have no significance outside the compiler. Cast is used to specify that data should be converted to a form consistent with a specified type (here a C int type).

The core of the FunctionCompile is the use of LibraryFunction, which is what actually calls the external library function that we declared with the library function declaration.

The last step in the function compiled by FunctionCompile is to extract data from the C array and return it as a Wolfram Language list. To do this requires the new function FromRawPointer, which actually retrieves data from a specified location in memory. (And, yes, this is a raw dereferencing operation that will cause a crash if it isn’t done correctly.)

All of this may at first seem rather complicated, but for what it’s doing, it’s remarkably simple—and greatly leverages the whole symbolic structure of the Wolfram Language. It’s also worth realizing that in this particular example, we’re just dipping into compiled code and then returning results. In larger-scale cases we’d be doing many more operations—typically specified directly by top-level Wolfram Language code—within compiled code, and so type declaration and conversion operations would be a smaller fraction of the code we have to write.

One feature of the example we’ve just looked at is that it only uses built-in types. But in Version 13.1 it’s now possible to define custom types, such as the analog of C structs. As an example, consider the function ldiv from the C standard library. This function returns an object of type ldiv_t, defined by the following typedef:

Here’s the Wolfram Language version of this declaration, based on setting up a "Product" type named "CLDivT":

&#10005

(The "ReferenceSemantics"→False option specifies that this type will actually be passed around as a value, rather than just a pointer to a value.)

Now the declaration for the ldiv function can use this new custom type:

&#10005

The final definition of the call to the external ldiv function is then:

&#10005

And now we can use the function (and, yes, it will be as efficient as if we’d directly written everything in C):

&#10005

The examples we’ve given here are very small ones. But the whole structure for external function calls that’s now in Version 13.1 is set up to handle large and complex situations—and indeed we’ve been using it internally with great success to set up important new built-in pieces of the Wolfram Language.

One of the elements that’s often needed in more complex situations is more sophisticated memory management, and our new "Managed" type provides a convenient and streamlined way to do this.

This makes a compiled function that creates an array of 10,000 machine integers:

&#10005

Running the function effectively “leaks” memory:

&#10005

But now define a version of the function in which the array is “managed”:

&#10005

Now the memory associated with the array is automatically freed when it is no longer referenced:

&#10005

Just Call That C Function! Direct Access to External Libraries (June 2023)

Let’s say you’ve got an external library written in C—or in some other language that can compile to a C-compatible library. In Version 13.3 there’s now foreign function interface (FFI) capability that allows you to directly call any function in the external library just using Wolfram Language code.

Here’s a very trivial C function:

This function happens to be included in compiled form in the compilerDemoBase library that’s part of Wolfram Language documentation. Given this library, you can use ForeignFunctionLoad to load the library and create a Wolfram Language function that directly calls the C addone function. All you need do is specify the library and C function, and then give the type signature for the function:

Now ff is a Wolfram Language function that calls the C addone function:

The C function addone happens to have a particularly simple type signature, that can immediately be represented in terms of compiler types that have direct analogs as Wolfram Language expressions. But in working with low-level languages, it’s very common to have to deal directly with raw memory, which is something that never happens when you’re purely working at the Wolfram Language level.

So, for example, in the OpenSSL library there’s a function called RAND_bytes, whose C type signature is:

And the important thing to notice is that this contains a pointer to a buffer buf that gets filled by RAND_bytes. If you were calling RAND_bytes from C, you’d first allocate memory for this buffer, then—after calling RAND_bytes—read back whatever was written to the buffer. So how can you do something analogous when you’re calling RAND_bytes using ForeignFunction in Wolfram Language? In Version 13.3 we’re introducing a family of constructs for working with pointers and raw memory.

So, for example, here’s how we can create a Wolfram Language foreign function corresponding to RAND_bytes:

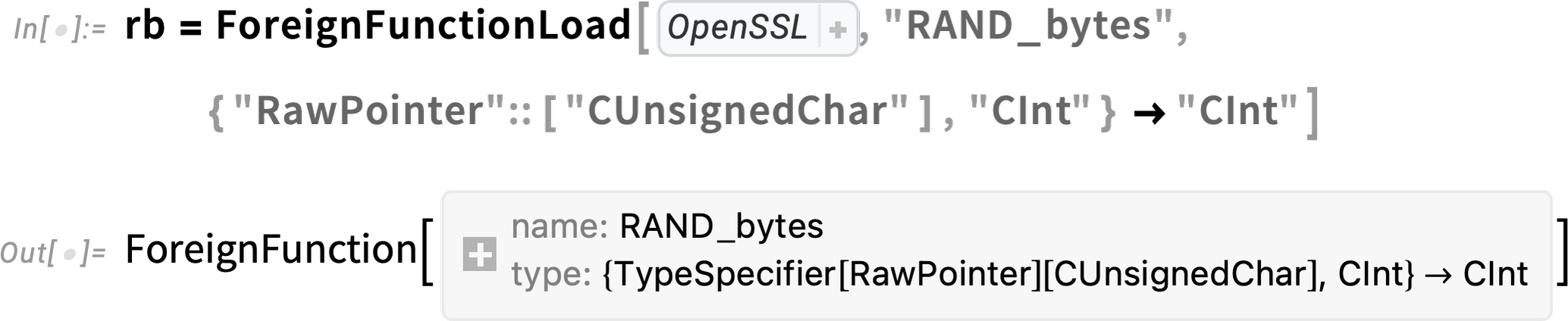
But to actually use this, we need to be able to allocate the buffer, which in Version 13.3 we can do with RawMemoryAllocate:

This creates a buffer that can store 10 unsigned chars. Now we can call rb, giving it this buffer:

rb will fill the buffer—and then we can import the results back into Wolfram Language:

There’s some complicated stuff going on here. RawMemoryAllocate does ultimately allocate raw memory—and you can see its hex address in the symbolic object that’s returned. But RawMemoryAllocate creates a ManagedObject, which keeps track of whether it’s being referenced, and automatically frees the memory that’s been allocated when nothing references it anymore.

Long ago languages like BASIC provided PEEK and POKE functions for reading and writing raw memory. It was always a dangerous thing to do—and it’s still dangerous. But it’s somewhat higher level in Wolfram Language, where in Version 13.3 there are now functions like RawMemoryRead and RawMemoryWrite. (For writing data into a buffer, RawMemoryExport is also relevant.)

Most of the time it’s very convenient to deal with memory-managed ManagedObject constructs. But for the full low-level experience, Version 13.3 provides UnmanageObject, which disconnects automatic memory management for a managed object, and requires you to explicitly use RawMemoryFree to free it.

One feature of C-like languages is the concept of a function pointer. And normally the function that the pointer is pointing to is just something like a C function. But in Version 13.3 there’s another possibility: it can be a function defined in Wolfram Language. Or, in other words, from within an external C function it’s possible to call back into the Wolfram Language.

Let’s use this C program:

You can actually compile it right from Wolfram Language using:

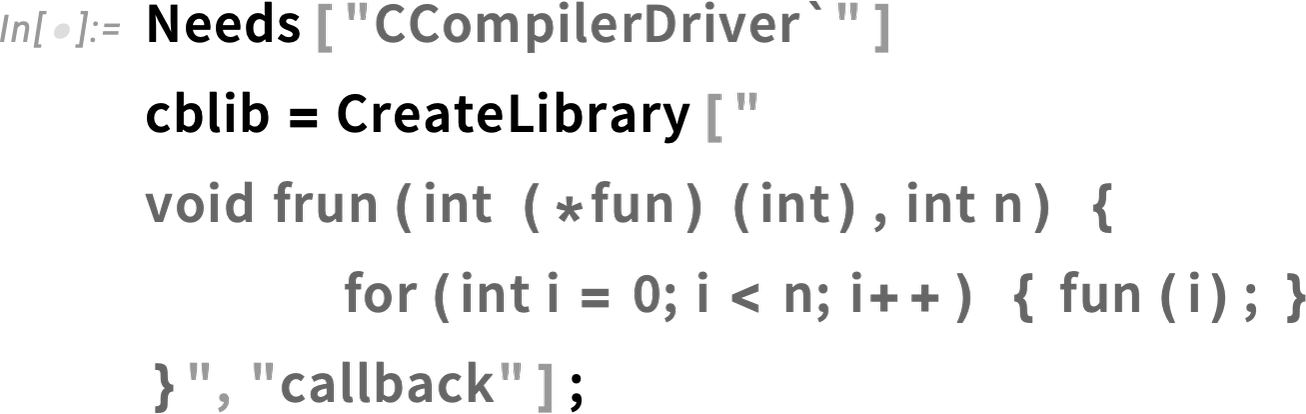
Now we load frun as a foreign function—with a type signature that uses "OpaqueRawPointer" to represent the function pointer:

What we need next is to create a function pointer that points to a callback to Wolfram Language:

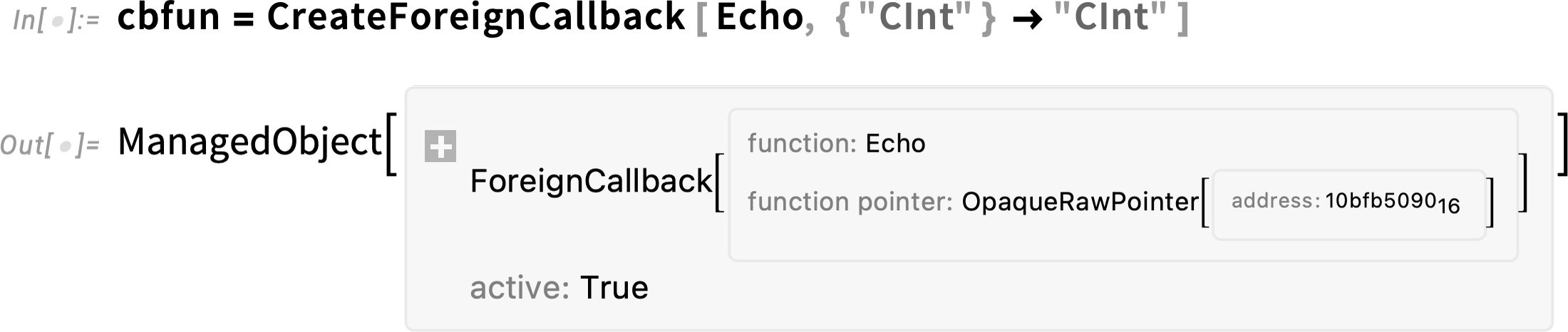
The Wolfram Language function here is just Echo. But when we call frun with the cbfun function pointer we can see our C code calling back into Wolfram Language to evaluate Echo:

ForeignFunctionLoad provides an extremely convenient way to call external C-like functions directly from top-level Wolfram Language. But if you’re calling C-like functions a great many times, you’ll sometimes want to do it using compiled Wolfram Language code. And you can do this using the LibraryFunctionDeclaration mechanism that was introduced in Version 13.1. It’ll be more complicated to set up, and it’ll require an explicit compilation step, but there’ll be slightly less “overhead” in calling the external functions.

Directly Compiling Function Definitions (June 2022)

If you have an explicit pure function (Function[...]) you can use FunctionCompile to produce a compiled version of it. But what if you have a function that’s defined using downvalues, as in:

&#10005

In Version 13.1 you can directly compile function definitions like this. But—as is the nature of compilation—you have declare what types are involved. Here is a declaration for the function fac that says it takes a single machine integer, and returns a machine integer:

&#10005

Now we can create a compiled function that computes fac[n]:

&#10005

The compiled function runs significantly faster than the ordinary symbolic definition:

&#10005

&#10005

The ability to declare and use downvalue definitions in compilation has the important feature that it allows you to write a definition just once, and then use it both directly, and in compiled code.

Manipulating Expressions in Compiled Code (June 2022)

An early focus of the Wolfram Language compiler is handling low-level “machine” types, such as integers or reals of certain lengths. But one of the advances in the Version 13.1 compiler is direct support for an "InertExpression" type for representing any Wolfram Language expression within compiled code.

When you use something like FunctionCompile, it will explicitly try to compile whatever Wolfram Language expressions it’s given. But if you wrap the expressions with InertExpression the compiler will then just treat the expressions as inert structural objects of type "InertExpression". This sets up a compiled function that constructs an expression (implicitly of type "InertExpression"):

Evaluating the function constructs and then returns the expression:

Normally, within the compiler, an "InertExpression" object will be treated in a purely structural way, without any evaluation (and, yes, it’s closely related to the "ExprStruct" data structure). But sometimes it’s useful to perform evaluation on it, and you can do this with InertEvaluate:

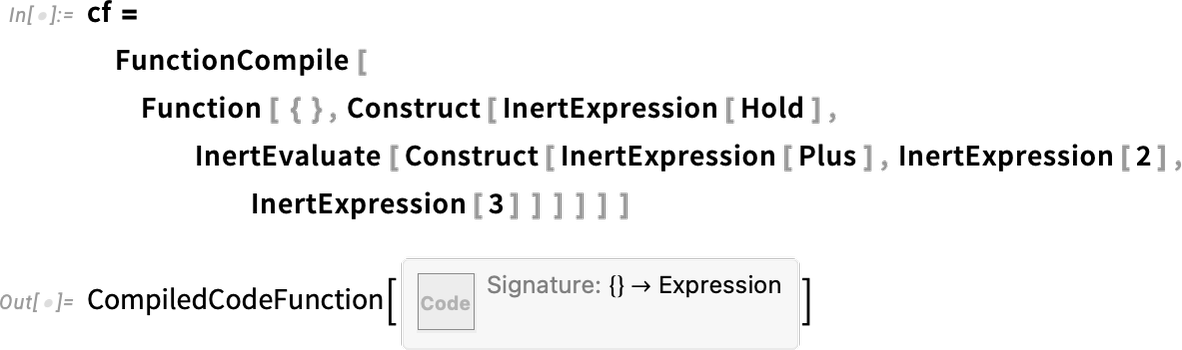
Now the InertEvaluate does the evaluation before wrapping Hold around the inert expression:

The ability to handle expressions directly in the compiler might seem like some kind of detail. But it’s actually hugely important in opening up possibilities for future development with the Wolfram Language. For the past 35 years, we’ve internally been able to write low-level expression manipulation code as part of the C language core of the Wolfram Language kernel. But the ability of the Wolfram Language compiler to handle expressions now opens this up—and lets anyone write maximally efficient code for manipulating expressions that interoperate with everything else in the Wolfram Language.

Mixing Compiled and Evaluated Code (December 2022)

We’ve worked hard to have code you write in the Wolfram Language immediately run efficiently. But by taking the extra one-time effort to invoke the Wolfram Language compiler—telling it more details about how you expect to use your code— you can often make your code run more efficiently, and sometimes dramatically so. In Version 13.2 we’ve been continuing the process of streamlining the workflow for using the compiler, and for unifying code that’s set up for compilation, and code that’s not.

The primary work you have to do in order to make the best use of the Wolfram Language compiler is in specifying types. One of the important features of the Wolfram Language in general is that a symbol x can just as well be an integer, a list of complex numbers or a symbolic representation of a graph. But the main way the compiler adds efficiency is by being able to assume that x is, say, always going to be an integer that fits into a 64-bit computer word.

The Wolfram Language compiler has a sophisticated symbolic language for specifying types. Thus, for example

is a symbolic specification for the type of a function that takes two 64-bit integers as input, and returns a single one. TypeSpecifier[ ... ] is a symbolic construct that doesn’t evaluate on its own, and can be used and manipulated symbolically. And it’s the same story with Typed[ ... ], which allows you to annotate an expression to say what type it should be assumed to be.

But what if you want to write code which can either be evaluated in the ordinary way, or fed to the compiler? Constructs like Typed[ ... ] are for permanent annotation. In Version 13.2 we’ve added TypeHint which allows you to give a hint that can be used by the compiler, but will be ignored in ordinary evaluation.

This compiles a function assuming that its argument x is an 8-bit integer:

By default, the 100 here is assumed to be represented as a 64-bit integer. But with a type hint, we can say that it too should be represented as an 8-bit integer:

150 doesn’t fit in an 8-bit integer, so the compiled code can’t be used:

But what’s relevant here is that the function we compiled can be used not only for compilation, but also in ordinary evaluation, where the TypeHint effectively just “evaporates”:

As the compiler develops, it’s going to be able to do more and more type inferencing on its own. But it’ll always be able to get further if the user gives it some hints. For example, if x is a 64-bit integer, what type should be assumed for x^x? There are certainly values of x for which x^x won’t fit in a 64-bit integer. But the user might know those won’t show up. And so they can give a type hint that says that the x^x should be assumed to fit in a 64-bit integer, and this will allow the compiler to do much more with it.

It’s worth pointing out that there are always going to be limitations to type inferencing, because, in a sense, inferring types requires proving theorems, and there can be theorems that have arbitrarily long proofs, or no proofs at all in a certain axiomatic system. For example, imagine asking whether the type of a zero of the Riemann zeta function has a certain imaginary part. To answer this, the type inferencer would have to solve the Riemann hypothesis. But if the user just wanted to assume the Riemann hypothesis, they could—at least in principle—use TypeHint.

TypeHint is a wrapper that means something to the compiler, but “evaporates” in ordinary evaluation. Version 13.2 adds IfCompiled, which lets you explicitly delineate code that should be used with the compiler, and code that should be used in ordinary evaluation. This is useful when, for example, ordinary evaluation can use a sophisticated built-in Wolfram Language function, but compiled code will be more efficient if it effectively builds up similar functionality from lower-level primitives.

In its simplest form FunctionCompile lets you take an explicit pure function and make a compiled version of it. But what if you have a function where you’ve already assigned downvalues to it, like:

Now in Version 13.2 you can use the new DownValuesFunction wrapper to give a function like this to FunctionCompile:

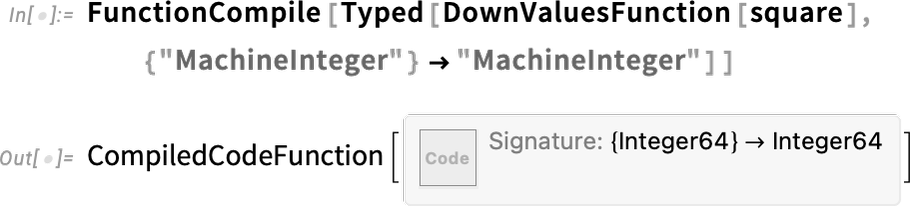
This is important because it lets you set up a whole network of definitions using := etc., then have them automatically be fed to the compiler. In general, you can use DownValuesFunction as a wrapper to tag any use of a function you’ve defined elsewhere. It’s somewhat analogous to the KernelFunction wrapper that you can use to tag built-in functions, and specify what types you want to assume for them in code that you’re feeding to the compiler.

Packaging Large-Scale Compiled Code (December 2022)

Let’s say you’re building a substantial piece of functionality that might include compiled Wolfram Language code, external libraries, etc. In Version 13.2 we’ve added capabilities to make it easy to “package up” such functionality, and for example deploy it as a distributable paclet.

As an example of what can be done, this installs a paclet called GEOSLink that includes the GEOS external library and compiler-based functionality to access this:

Now that the paclet is installed, we can use a file from it to set up a whole collection of functions that are defined in the paclet:

Given the code in the paclet we can now just start calling functions that use the GEOS library:

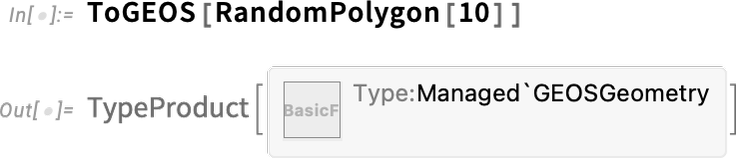
It’s quite nontrivial that this “just works”. Because for it to work, the system has to have been told to load and initialize the GEOS library, as well as convert the Wolfram Language polygon geometry to a form suitable for GEOS. The returned result is also nontrivial: it’s essentially a handle to data that’s inside the GEOS library, but being memory-managed by the Wolfram Language system. Now we can take this result, and call a GEOS library function on it, using the Wolfram Language binding that’s been defined for that function:

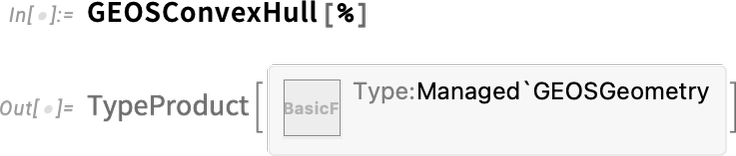
This gets the result “back from GEOS” into pure Wolfram Language form:

How does all this work? This goes to the directory for the installed GEOSLink paclet on my system:

&#10005

There’s a subdirectory called LibraryResources that contains dynamic libraries suitable for my computer system:

&#10005

The libgeos libraries are the raw external GEOS libraries “from the wild”. The GEOSLink library is a library that was built by the Wolfram Language compiler from Wolfram Language code that defines the “glue” for interfacing between the GEOS library and the Wolfram Language:

&#10005

What is all this? It’s all based on new functionality in Version 13.2. And ultimately what it’s doing is to create a CompiledComponent construct (which is a new thing in Version 13.2). A CompiledComponent construct represents a bundle of compilable functionality with elements like "Declarations", "InstalledFunctions", "LibraryFunctions", "LoadingEpilogs" and "ExternalLibraries". And in a typical case—like the one shown here—one creates (or adds to) a CompiledComponent using DeclareCompiledComponent.

Here’s an example of part of what’s added by DeclareCompiledComponent:

&#10005

First there’s a declaration of an external (in this case GEOS) library function, giving its type signature. Then there’s a declaration of a compilable Wolfram Language function GEOSUnion that directly calls the GEOSUnion function in the external library, defining it to take a certain memory-managed data structure as input, and return a similarly memory-managed object as output.

From this source code, all you do to build an actual library is use BuildCompiledComponent. And given this library you can start calling external GEOS functions directly from top-level Wolfram Language code, as we did above.

But the CompiledComponent object does something else as well. It also sets up everything you need to be able to write compilable code that calls the same functions as you can within the built library.

The bottom line is that with all the new functionality in Version 13.2 it’s become dramatically easier to integrate compiled code, external libraries etc. and to make them conveniently distributable. It’s a fairly remarkable simplification of what was previously a time-consuming and complex software engineering challenge. And it’s good example of how powerful it can be to set up symbolic specifications in the Wolfram Language and then use our compiler technology to automatically create and deploy code defined by them.

The Advance of the Compiler Continues (June 2023)

For several years we’ve had an ambitious project to develop a large-scale compiler for the Wolfram Language. And in each successive version we’re further extending and enhancing the compiler. In Version 13.3 we’ve managed to compile more of the compiler itself (which, needless to say, is written in Wolfram Language)—thereby making the compiler more efficient in compiling code. We’ve also enhanced the performance of the code generated by the compiler—particularly by optimizing memory management done in the compiled code.

Over the past several versions we’ve been steadily making it possible to compile more and more of the Wolfram Language. But it’ll never make sense to compile everything—and in Version 13.3 we’re adding KernelEvaluate to make it more convenient to call back from compiled code to the Wolfram Language kernel.

Here’s an example:

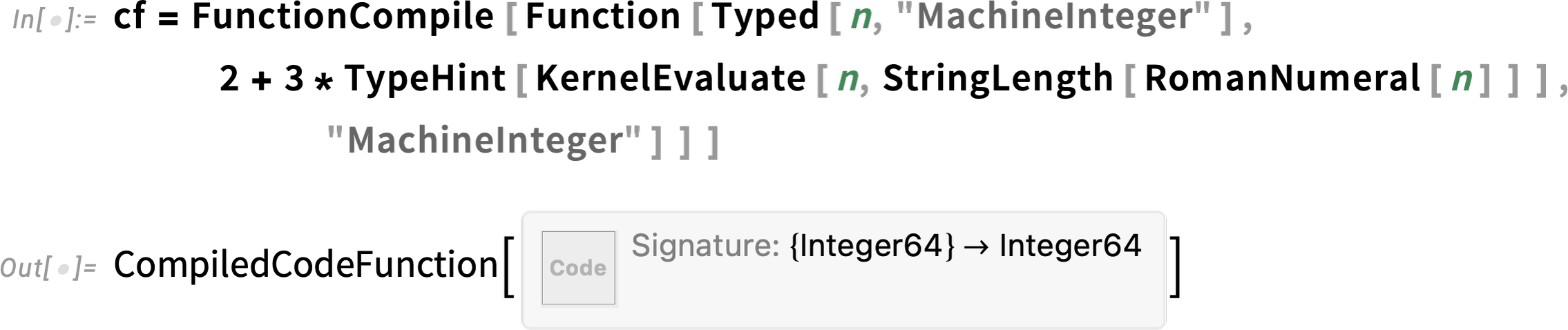
We’ve got an argument n that’s declared as being of type MachineInteger. Then we’re doing a computation on n in the kernel, and using TypeHint to specify that its result will be of type MachineInteger. There’s at least arithmetic going on outside the KernelEvaluate that can be compiled, even though the KernelEvaluate is just calling uncompiled code:

There are other enhancements to the compiler in Version 13.3 as well. For example, Cast now allows data types to be cast in a way that directly emulates what the C language does. There’s also now SequenceType, which is a type analogous to the Wolfram Language Sequence construct—and able to represent an arbitrary-length sequence of arguments to a function.

Controlling Runaway Computations (December 2022)

Back in 1979 when I started building SMP—the forerunner to the Wolfram Language—I did something that to some people seemed very bold, perhaps even reckless: I set up the system to fundamentally do “infinite evaluation”, that is, to continue using whatever definitions had been given until nothing more could be done. In other words, the process of evaluation would always go on until a fixed point was reached. “But what happens if x doesn’t have a value, and you say x = x + 1?” people would ask. “Won’t the system blow up in that case?” Well, in some sense yes. But I took a calculated gamble that the benefits of infinite evaluation for ordinary computations that people actually want to do would vastly outweigh any possible issues with what seemed like “pointless corner cases” such as x = x + 1. Well, 43 years later I think I can say with some confidence that that gamble worked out. The concept of infinite evaluation—combined with the symbolic structure of the Wolfram Language—has been a source of tremendous power, and most users simply never run into, and never have to think about, the x = x + 1 “corner case”.

However, if you type x = x + 1 the system clearly has to do something. And in a sense the purest thing to do would just be to continue computing forever. But 34 years ago that led to a rather disastrous problem on actual computers—and in fact still does today. Because in general this kind of repeated evaluation is a recursive process, that ultimately has to be implemented using the call stack set up for every instance of a program by the operating system. But the way operating systems work (still!) is to allocate only a fixed amount of memory for the stack—and if this is overrun, the operating system will simply make your program crash (or, in earlier times, the operating system itself might crash). And this meant that ever since Version 1, we’ve needed to have a limit in place on infinite evaluation. In early versions we tried to give the “result of the computation so far”, wrapped in Hold. Back in Version 10, we started just returning a held version of the original expression:

But even this is in a sense not safe. Because with other infinite definitions in place, one can end up with a situation where even trying to return the held form triggers additional infinite computational processes.

In recent times, particularly with our exploration of multicomputation, we’ve decided to revisit the question of how to limit infinite computations. At some theoretical level, one might imagine explicitly representing infinite computations using things like transfinite numbers. But that’s fraught with difficulty, and manifest undecidability (“Is this infinite computation output really the same as that one?”, etc.) But in Version 13.2, as the beginning of a new, “purely symbolic” approach to “runaway computation” we’re introducing the construct TerminatedEvaluation—that just symbolically represents, as it says, a terminated computation.

So here’s what now happens with x = x + 1:

A notable feature of this is that it’s “independently encapsulated”: the termination of one part of a computation doesn’t affect others, so that, for example, we get:

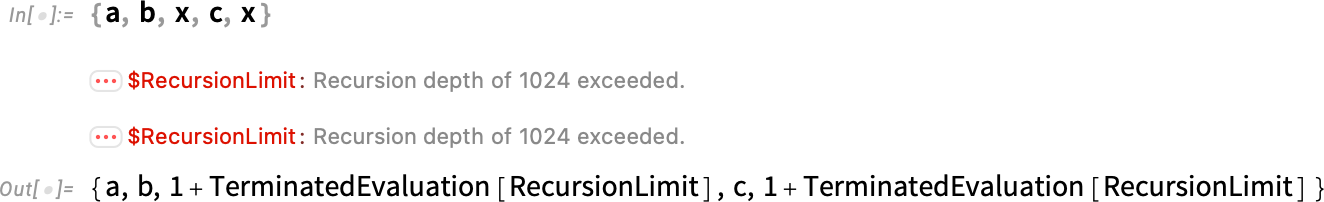
There’s a complicated relation between terminated evaluations and lazy evaluation, and we’re working on some interesting and potentially powerful new capabilities in this area. But for now, TerminatedEvaluation is an important construct for improving the “safety” of the system in the corner case of runaway computations. And introducing it has allowed us to fix what seemed for many years like “theoretically unfixable” issues around complex runaway computations.

TerminatedEvaluation is what you run into if you hit system-wide “guard rails” like $RecursionLimit. But in Version 13.2 we’ve also tightened up the handling of explicitly requested aborts—by adding the new option PropagateAborts to CheckAbort. Once an abort has been generated—either directly by using Abort[ ], or as the result of something like TimeConstrained[ ] or MemoryConstrained[ ]—there’s a question of how far that abort should propagate. By default, it’ll propagate all the way up, so your whole computation will end up being aborted. But ever since Version 2 (in 1991) we’ve had the function CheckAbort, which checks for aborts in the expression it’s given, then stops further propagation of the abort.

But there was always a lot of trickiness around the question of things like TimeConstrained[ ]. Should aborts generated by these be propagated the same way as Abort[ ] aborts or not? In Version 13.2 we’ve now cleaned all of this up, with an explicit option PropagateAborts for CheckAbort. With PropagateAborts→True all aborts are propagated, whether initiated by Abort[ ] or TimeConstrained[ ] or whatever. PropagateAborts→False propagates no aborts. But there’s also PropagateAborts→Automatic, which propagates aborts from TimeConstrained[ ] etc., but not from Abort[ ].

Streamlining Parallel Computation (June 2023)

Ever since the mid-1990s there’s been the capability to do parallel computation in the Wolfram Language. And certainly for me it’s been critical in a whole range of research projects I’ve done. I currently have 156 cores routinely available in my “home” setup, distributed across 6 machines. It’s sometimes challenging from a system administration point of view to keep all those machines and their networking running as one wants. And one of the things we’ve been doing in recent versions—and now completed in Version 13.3—is to make it easier from within the Wolfram Language to see and manage what’s going on.

It all comes down to specifying the configuration of kernels. And in Version 13.3 that’s now done using symbolic KernelConfiguration objects. Here’s an example of one:

There’s all sorts of information in the kernel configuration object:

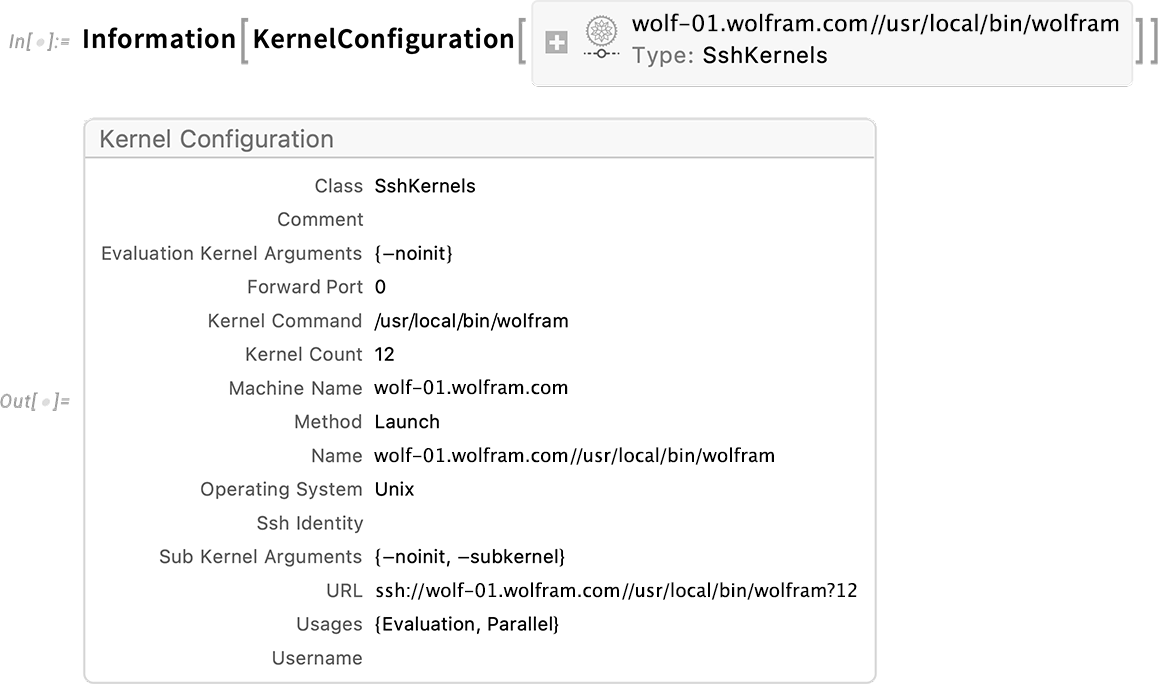
It describes “where” a kernel with that configuration will be, how to get to it, and how it should be launched. The kernel might just be local to your machine. Or it might be on a remote machine, accessible through ssh, or https, or our own wstp (Wolfram Symbolic Transport Protocol) or lwg (Lightweight Grid) protocols.

In Version 13.3 there’s now a GUI for setting up kernel configurations:

The Kernel Configuration Editor lets you enter all the details that are needed, about network connections, authentication, locations of executables, etc.

But once you’ve set up a KernelConfiguration object, that’s all you ever need—for example to say “where” to do a remote evaluation:

ParallelMap and other parallel functions then just work by doing their computations on kernels specified by a list of KernelConfiguration objects. You can set up the list in the Kernels Settings GUI:

Here’s my personal default collection of parallel kernels:

This now counts the number of individual kernels running on each machine specified by these configurations:

In Version 13.3 a convenient new feature is named collections of kernels. For example, this runs a single “representative” kernel on each distinct machine: