Learn Multivariable Calculus through Incredible Visualizations with Wolfram Language

Multivariable calculus extends calculus concepts to functions of several variables and is an essential tool for modeling and regression analysis in economics, engineering, data science and other fields. Learning multivariable calculus is also the first step toward advanced calculus and follows single-variable calculus courses. Wolfram Language provides world-class functionality for the computation and visualization of concepts, which makes this elegant body of mathematical knowledge easy and fun to learn!
Today, I am proud to announce a free interactive course, Introduction to Multivariable Calculus, that will help students all over the world learn to master this difficult but highly applicable branch of mathematics. This comprehensive multivariable calculus course extends the notions of limits, derivatives and integrals to higher dimensions. It also considers constrained and unconstrained optimization problems and explores the “three great theorems” of multivariable calculus. For anyone who has not yet taken a single-variable calculus course, the popular Wolfram U course Introduction to Calculus covers equivalent material to an introductory college-level calculus course and the AP Calculus AB course.
Ready to get started? Click the following image to begin exploring the interactive course before reading the rest of this blog post.
Overview
Students taking this course will receive a thorough introduction to multivariable calculus. This includes standard topics like vectors, limits and partial derivatives as well as some of the great theorems of calculus. Introduction to Multivariable Calculus will also discuss some more advanced topics, like triple integrals, curl and divergence, and parametric surfaces.
Here is a sneak peek at some of the course topics (shown in the left-hand column):

Multivariable calculus is a vast subject, but I wanted to keep the course at a reasonable length. I expect students can finish watching the 36 videos and complete the five quizzes in about nine hours.
This course builds on the foundations of single-variable calculus, so it is recommended to have a strong understanding of that subject. Anyone who has completed an AP Calculus class will already be well equipped for this course.
The next few sections of this blog post will describe the different components of the course in greater detail.
Lessons
The core of the course is a set of 36 lessons, beginning with “What Is Multivariable Calculus?” This introductory lesson includes a discussion about what multivariable calculus is and an overview of what is covered in the course. This is followed by a few simple examples comparing single-variable concepts to their analogs in multivariable calculus, a list of multivariable calculus’s applications and a brief account of the historical roots of multivariable calculus in the works of Gauss, Maxwell, Gibbs and others. The lesson concludes with a discussion about who this course is for and how to approach it.
Later lessons begin with a review of how each new topic fits into the overall course as well as the field of calculus, followed by a discussion of the key concepts, with interspersed examples illustrating the main ideas. Wolfram Language functions are used throughout to verify solutions or visualize concepts.
The videos range from five to 24 minutes in length, and each video is accompanied by a transcript notebook displayed on the right-hand side of the screen. Copy and paste Wolfram Language input directly from the transcript notebook to the embedded scratch notebook to try the examples for yourself.
Exercises
Each lesson comes with a set of six exercises to put the concepts learned in the lesson into practice. Exercises are not graded, and each comes with a detailed solution. The following shows an exercise from lesson 35 on Stokes’s theorem:


The exercise notebooks are interactive, so students can experiment with each problem in the Wolfram Cloud. They are encouraged to attempt the problem themselves and can copy the Wolfram Language code in order to manipulate variables or use the code for other similar problems.
Problem Sets
Each section contains a set of 14 practice problems with detailed solutions. These example problems make use of the concepts and tools learned in the section. They are meant to reinforce the material, so students can use the concepts to solve real problems:

Quizzes
Each section of the course ends with a short, multiple-choice quiz with 10 problems. The quiz problems are roughly at the same level as those discussed in the lessons, and a student who reviews the section carefully should be well prepared to pass the quiz:

Students receive instant feedback about their quiz question responses, and they are encouraged to try any method, including hand or computer calculations, to solve them.
Illuminating Illustrations with the Power of Wolfram
One of the biggest advantages of writing this course in Wolfram Notebooks is the ability to make three-dimensional, interactive visualizations that intuitively explain topics like spherical coordinates, curl and divergence, vector fields, flux integrals and more. Here’s a selection of some of the visualizations in this course.
An interactive figure simultaneously showing curves of steepest ascent on a contour map and an interactive three-dimensional plot:

An interface that shows a transformation between two different coordinate systems:

A visualization of the volume element ![]() in spherical coordinates:
in spherical coordinates:

Visualizing the process of iterated integration in spherical coordinates:

A visualization that helps to understand the idea of curve orientation:
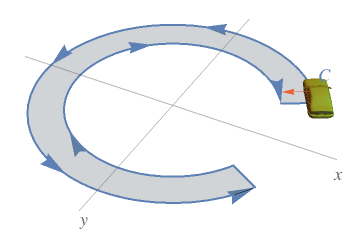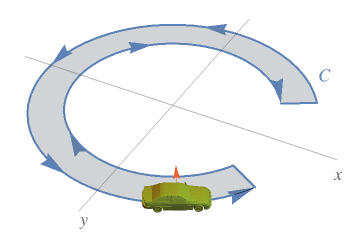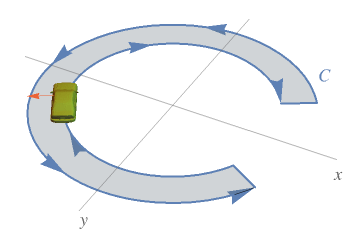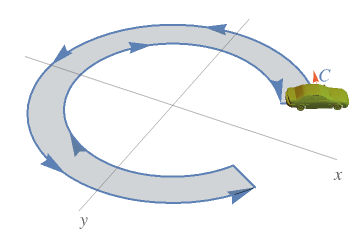
What Our Students Are Saying
Wolfram U recently shared an early version of this course with a group of 185 students in a Daily Study Group series. In addition to the valuable suggestions and feedback we received, students had a lot of positive things to say about this course—here is a brief selection of their comments:
- “Wolfram U has really raised the bar this year, but this class has set the standard—in every which way. It really showcases the power of Mathematica, has fantastic and useful coding examples with lots of applications, and—by the way—teaches multivariable calculus. A refresher course in the way I wish I could have studied it the first time.”
- “This is probably the best-looking course out there. The graphic examples are great and engaging. The examples are a great teaching resource for me as well.”
- “These are the best lectures with wonderful visualizations which make it so much easier to grasp the material. Thanks to all those who are making it available.”
- “I think this is a first-rate course. The visuals are crisp, clean and informative.”
- “The course is interesting and well structured; it is very useful to have practice problem sets before the quizzes. The visualizations/graphics are really impressive.”
- “Great. Really great. This is an exercise in understanding the big picture and then applying it in the trenches. There are more juicy examples in this course than most. You definitely want to take Tim’s material apart and see how he does those things.”
- “Best course I’ve taken on Wolfram U, and I’ve taken quite a few!”
Course Certificate
Students should watch all the lessons and attempt the quizzes in the recommended sequence because course topics often build on earlier concepts and techniques. At the end of the course, students can request a certificate of completion. A course certificate is earned after watching all the lessons and passing all the quizzes. It represents proficiency in the fundamentals of multivariable calculus and adds value to a résumé or social media profile.

Also, an optional final exam is available at the end of the course. Students can receive an advanced level of certification by passing this exam.
A Building Block for Success
Mastering the techniques of multivariable calculus is important for learners and students in fields involving data, including science, business and machine learning. It is important to develop a strong intuition and understanding of the concepts. That is why I have included a lot of specialized graphics that are designed to make difficult concepts more accessible and more memorable. I hope that Introduction to Multivariable Calculus will help learners achieve mastery and contribute to success in their chosen fields. I enjoyed creating and teaching this course and welcome any comments regarding the current course as well as suggestions for future courses.
About the Author
This course is taught by Timothy McDevitt, who teaches multivariable calculus at Elizabethtown College almost every semester, and it is his favorite course to teach. McDevitt has bachelor’s degrees in math and physics as well as a master’s and doctorate in applied mathematics from the University of Virginia.
In addition to being a visualization developer at Wolfram Research since 2018, he previously worked with NASA and the US Navy and and was a 2021–2022 Congressional Fellow representing the American Statistical Association.
Acknowledgements
This course is the result of the work of the Wolfram U and Algorithms R&D teams. I would like to thank Devendra Kapadia, Brett Champion, Joaquin Orozco, Anisha Basil, Joyce Tracewell, Abrita Chakravarty, Arben Kalziqi, Luke Titus, Matt Coleman, Mariah Laugesen, Laura Crawford and Marco Saragnese for all the work they put into getting this course up and running.
| Register for one of Wolfram U’s Daily Study Groups. |



The transcripts do not appear to be listed with the lessons right now. I used the transcripts when studying the EIWL course. That course had a “transcripts” tab for each lesson. Is this course set up differently?
I believe 9 hours is hopelessly optimistic for students taking this course. The Daily Study Group ran for 15 hours. Those sessions were efficient, but they didn’t include any work on exercises. I audited the Daily Study Group; I plan to go through all the videos and perform the exercises. I am estimating ~27 hours for completing the course. I’ll provide feedback here when I’m done (and hopefully pass the quizzes and final).
Very interesting, instructive and beautiful!