Two years ago we released Version 12.0 of the Wolfram Language. Here are the updates in geography since then, including the latest features in 13.0. The contents of this post are compiled from Stephen Wolfram’s Release Announcements for 12.1, 12.2, 12.3 and 13.0.

Geo-everything (March 2020)

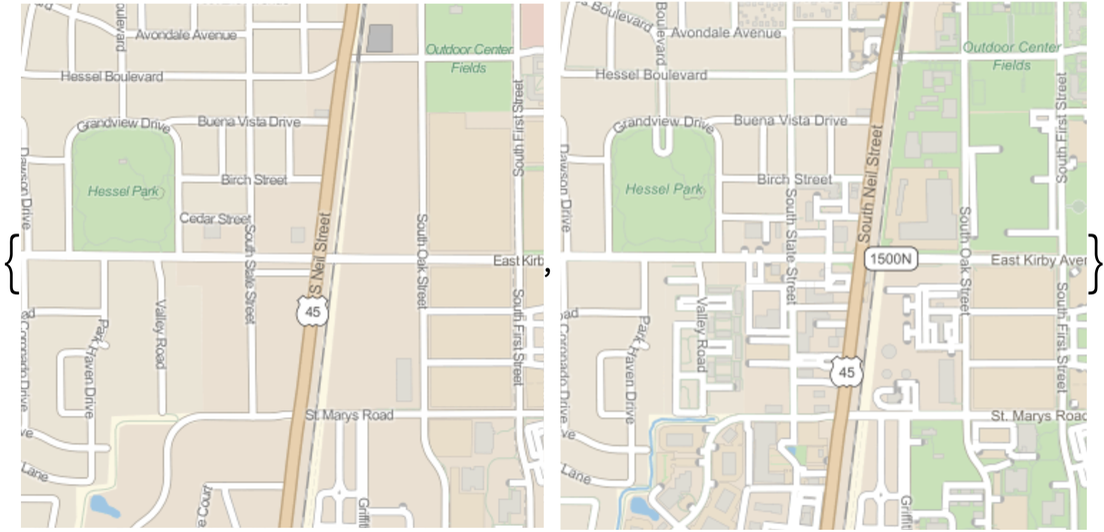
The Wolfram Language knows about many things. One of them is geography. And in Version 12.1 we’ve substantially updated and expanded our sources of geographic data (as well as upgrading our server-based algorithms). So, for example, the level of detail available in typical maps has increased substantially:

For many years now we’ve had outstanding geodetic computation in the Wolfram Language. And we also have excellent computational geometry for doing all sorts of computations on regions in Euclidean space. But of course the Earth is not flat, and one of the achievements of Version 12.1 is to bring our region-computation capabilities to the geo domain, handling non-flat regions.

It’s an interesting exercise in geometry. We have things like the polygon of the United States defined in geo coordinates—as a lat-long region on the Earth. But to use our computational geometry capabilities we need to make it something purely Euclidean. But we can do that by using our geodesy capabilities to embed it in full 3D space.

So now we can just compute the centroid of the region that is the US:

&#10005 RegionCentroid[Polygon[Entity["Country", "UnitedStates"]]]

That third element in the geo position is a depth (in meters), and reflects the curvature of the US polygon. And, actually, we can see this directly too:

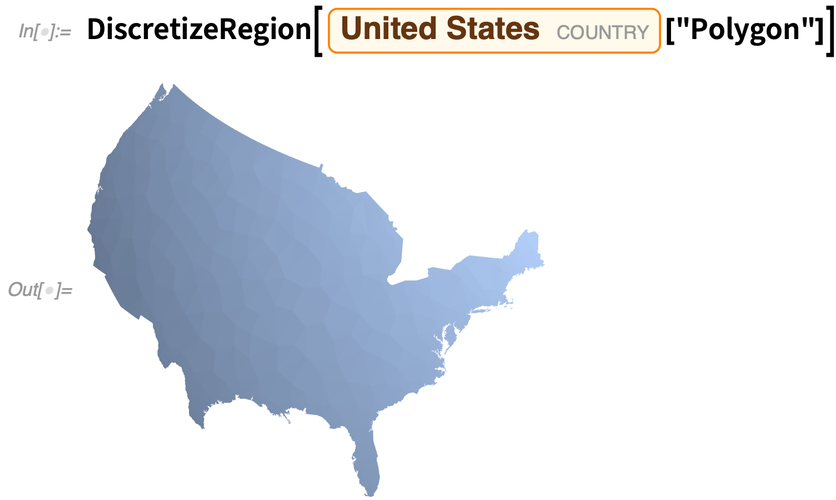
&#10005 DiscretizeRegion[Entity["Country", "UnitedStates"]["Polygon"]]

This is a 3D object, so we can rotate it to see the curvature more clearly:

We can also work the other way around: taking geo regions and projecting them onto a flat map, then computing with them. One knows that Greenland looks very different sizes with different map projections. Here’s its “map area” in the Mercator projection (in units of degrees-squared):

&#10005 Area[GeoGridPosition[Entity["Country", "Greenland"]["Polygon"], "Mercator"]]

But here it is (also in degrees-squared) in an area-preserving projection:

&#10005 Area[GeoGridPosition[Entity["Country", "Greenland"]["Polygon"], "CylindricalEqualArea"]]

And as part of the effort to make “geo everything”, Version 12.1 also includes GeoDensityPlot and GeoContourPlot.

New in Geo (December 2020)

Want to analyze a document that’s in PDF? We’ve been able to extract basic content from PDF files for well over a decade. But PDF is a highly complex (and evolving) format, and many documents “in the wild” have complicated structures. In Version 12.2, however, we’ve dramatically expanded our PDF import capabilities, so that it becomes realistic to, for example, take a random paper from arXiv, and import it:

&#10005 Import["https://arxiv.org/pdf/2011.12174.pdf"]

By default, what you’ll get is a high-resolution image for each page (in this particular case, all 100 pages).

If you want the text, you can import that with "Plaintext":

&#10005 Import["https://arxiv.org/pdf/2011.12174.pdf", "Plaintext"]

Now you can immediately make a word cloud of the words in the paper:

&#10005 WordCloud[%]

This picks out all the images from the paper, and makes a collage of them:

&#10005 ImageCollage[Import["https://arxiv.org/pdf/2011.12174.pdf", "Images"]]

You can get the URLs from each page:

&#10005 Import["https://arxiv.org/pdf/2011.12174.pdf", "URLs"]

Now pick off the last two, and get images of those webpages:

&#10005 WebImage /@ Take[Flatten[Values[%]], -2]

Depending on how they’re produced, PDFs can have all sorts of structure. "ContentsGraph" gives a graph representing the overall structure detected for a document:

&#10005 Import["https://arxiv.org/pdf/2011.12174.pdf", "ContentsGraph"]

And, yes, it really is a graph:

&#10005 Graph[EdgeList[%]]

For PDFs that are fillable forms, there’s more structure to import. Here I grabbed a random unfilled government form from the web. Import gives an association whose keys are the names of the fields—and if the form had been filled in, it would have given their values too, so you could immediately do analysis on them:

&#10005 Import["https://www.fws.gov/forms/3-200-41.pdf", "FormFieldRules"]

New, Crisper Geographic Maps (December 2021)

Maps involve a lot of data, and efficiently delivering them and rendering them (in appropriate projections, etc.) is a difficult matter. In Version 13.0 we’re greatly “crispening” maps, by using vector fonts for all labeling:

&#10005

At least for right now, by default the background is still a bitmap. You can use “crispened” vector graphics for the background as well—but it will take longer to render:

&#10005

One advantage of using vector labels is that they can work in all geo projections (note that in Version 13 if you don’t specify the region for GeoGraphics, it’ll default to the whole world):

&#10005

Another addition in Version 13 is the ability to mix multiple background layers. Here’s an example that includes a street map with a translucent relief map on top (and labels on top of that):

&#10005