The sparse ruler problem has been famously worked on by Paul Erdős, Marcel J. E. Golay, John Leech, Alfréd Rényi, László Rédei and Solomon W. Golomb, among many others. The problem is this: what is the smallest subset of so that the unsigned pairwise differences of give all values from 1 to ? One way to look at this is to imagine a blank yardstick. At what positions on the yardstick would you add 10 marks, so that you can measure any number of inches up to 36?

Another simple example is of size 3, which has differences , and . The sets of size 2 have only one difference. The minimal subset is not unique; the differences of also give .

Part of what makes the sparse ruler problem so compelling is its embodiment in an object inside every schoolchild’s desk—and its enduring appeal lies in its deceptive simplicity. Read on to see precisely just how complicated rulers, marks and recipes can be.

Some History

First, let’s review the rules and terminology used in the sparse ruler problem. A subset of a set covers if .

For example, what is the smallest subset of that covers the set ? The greatest number of differences for a subset of size 5 is , which is not enough to get 13 values. But a subset of size 6, with differences, is large enough. In this case, the subset covers , and so the size of the smallest covering subset of is at most 6.

Here are the differences using only :

Engage with the code in this post by downloading the Wolfram Notebook

&#10005 {1, 13, 9, 13, 6, 6, 13, 9, 9, 11, 11, 13, 13} - {0, 11, 6, 9, 1, 0, 6, 1, 0, 1, 0, 1, 0}

Of the 15 differences, two are achieved twice: and . Here is a way to list the pairs explicitly:

&#10005 Column[SplitBy[ SortBy[Subsets[{0, 1, 6, 9, 11, 13}, {2}], Differences], Differences]]

Let’s try another way to calculate the set of differences:

&#10005 Union@Abs@ Flatten@Outer[Subtract, {0, 1, 6, 9, 11, 13}, {0, 1, 6, 9, 11, 13}]

Of the subsets that cover , let be the size of a smallest subset (there may be more than one).

The following table summarizes the values of for . Both and of size 3 cover ; note that after sorting:

&#10005 Text@Grid[Prepend[Table[With[{ruler = SplitToRuler[sparsedata[[n]]]}, {ruler, Row[{"[", n, "]"}], Length[ruler]}], {n, 1, 12}], {"a smallest\n subset\n", "differences [n]", Row[{" the smallest\nsubset size ", Style[Subscript["M", "n"], Italic], "\n"}]}]]

In 1956, John Leech wrote “On the Representation of 1, 2, …, n by Differences,” which proved the bounds .
There are a few terms and “rules” to keep in mind when discussing the sparse ruler problem:

• A subset of containing 0 and is called an -length ruler, and its elements are called marks. (The length can be dropped when it is understood.)
• An -length ruler is complete if the distances between marks cover .
• A sparse ruler (or minimal complete ruler) is a length- complete ruler such that no length- ruler with fewer marks exists. An example of a sparse ruler is .
• An optimal ruler is a sparse ruler where there is no longer sparse ruler with the same number of marks. An example is . No longer sparse ruler with five marks exists.
• A perfect ruler is a sparse ruler where a longer sparse ruler with fewer marks does not exist. All sparse rulers of length less than 135 are perfect.
• A nonperfect ruler is a sparse ruler where a longer sparse ruler with fewer marks does exist.

This length-135 sparse ruler is nonperfect:

&#10005 Length@{0, 1, 2, 3, 4, 5, 6, 65, 68, 71, 74, 81, 88, 95, 102, 109, 116, 123, 127, 131, 135}

This length-138 sparse ruler is optimal:

&#10005 Length@{0, 1, 2, 3, 7, 14, 21, 28, 43, 58, 73, 88, 103, 111, 119, 127, 135, 136, 137, 138}

Here is an optimal length-50 sparse ruler with 12 marks (i.e. ). The list of positions of the marks is the ruler form:

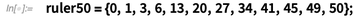
&#10005 ruler50 = {0, 1, 3, 6, 13, 20, 27, 34, 41, 45, 49, 50};

This visualizes the marks:

&#10005 Graphics[{ Thickness[.005], Line[{{#, 1}, {#, 1.5}}] & /@ Range@50, Line[{{#, 1}, {#, 5}}] & /@ ruler50 }, Axes -> {True, False}, Ticks -> {ruler50, None}, ImageSize -> 520]

Let the differences between the marks be the diff form. Here is the diff form for ruler50:

&#10005 Differences[ruler50]

In 1963, B. Wichmann wrote “A Note on Restricted Difference Bases,” in which he constructed many sparse rulers. The following code has his original recipe and a function to read the recipe:

&#10005 originalwichmannrecipe = { {1, 1 + r, 1 + 2 r, 3 + 4 r, 2 + 2 r, 1}, {r, 1, r, s, 1 + r, r}};

&#10005 WichmannRuler[recipe_, {x_, y_}] := Transpose[ Select[Transpose[recipe /. Thread[{r, s} -> {x, y}]], Min[#] > 0 &]]

With that, we can set up function for Wichmann recipe #1:

&#10005 Subscript[W, 1][r_, s_] := WichmannRuler[originalwichmannrecipe, {r, s}];

There are thousands of Wichmann recipes. Here’s the second:

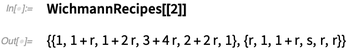
&#10005 WichmannRecipes[[2]]

Here’s a function for Wichmann recipe #2:

&#10005 Subscript[W, 2][r_, s_] := WichmannRuler[WichmannRecipes[[2]], {r, s}];

Here, and in the recipes are replaced by 1 and 5, respectively. These representations are examples of the split form of a sparse ruler:

&#10005 Column[{Subscript[W, 1][1, 5], Subscript[W, 2][1, 5]}]

We can use these functions to convert among the three forms of sparse ruler:

&#10005 DiffToRuler[diff_] := FoldList[Plus, 0, diff]

&#10005 DiffToSplit[diff_] := {First /@ Split[diff], Length /@ Split[diff]}

&#10005 SplitToDiff[split_] := Flatten[Table[#[[1]], {#[[2]]}] & /@ Transpose[split]]

&#10005 SplitToRuler[split_] := DiffToRuler[SplitToDiff[split]]

&#10005 RulerToSplit[ruler_] := DiffToSplit[Differences[ruler]]

Here are the diff forms for both and ruler50 from above; we can see from their identical outputs that they are in fact the same ruler:

&#10005 SplitToDiff[Subscript[W, 1][1, 5]]

&#10005 Differences[ruler50]

The diff form can be used to remake the ruler:

&#10005 DiffToRuler[%]

Here is the split form again:

&#10005 Subscript[W, 1][1, 5]

The split form can be written compactly and compared to Wichmann’s recipe with :

&#10005 TraditionalForm@ Grid[{HoldForm[#1^#2] & @@@ First@*Tally /@ Split@Differences[ruler50], HoldForm[#1^#2] & @@@ Transpose[originalwichmannrecipe]}, Frame -> All]

This Wichmann ruler is one of an infinite list of Wichmann rulers. The length-57 sparse rulers show two examples for :

&#10005 Text@Grid[{{"length", "marks", "recipe", Style["r", Italic], Style["s", Italic]}, {50, 12, "\!\(\*SuperscriptBox[\(1\), \(1\)]\) \!\(\*SuperscriptBox[\(2\), \ \(1\)]\) \!\(\*SuperscriptBox[\(3\), \(1\)]\) \ \!\(\*SuperscriptBox[\(7\), \(5\)]\) \!\(\*SuperscriptBox[\(4\), \ \(2\)]\) \!\(\*SuperscriptBox[\(1\), \(1\)]\)", 1, 5}, {57, 13, "\!\(\*SuperscriptBox[\(1\), \(1\)]\) \!\(\*SuperscriptBox[\(2\), \ \(1\)]\) \!\(\*SuperscriptBox[\(3\), \(1\)]\) \ \!\(\*SuperscriptBox[\(7\), \(6\)]\) \!\(\*SuperscriptBox[\(4\), \ \(2\)]\) \!\(\*SuperscriptBox[\(1\), \(1\)]\)", 1, 6}, {57, 13, "\!\(\*SuperscriptBox[\(1\), \(2\)]\) \!\(\*SuperscriptBox[\(3\), \ \(1\)]\) \!\(\*SuperscriptBox[\(5\), \(2\)]\) \ \!\(\*SuperscriptBox[\(11\), \(2\)]\) \!\(\*SuperscriptBox[\(6\), \(3\ \)]\) \!\(\*SuperscriptBox[\(1\), \(2\)]\)", 2, 2}, {90, 16, "\!\(\*SuperscriptBox[\(1\), \(2\)]\) \!\(\*SuperscriptBox[\(3\), \ \(1\)]\) \!\(\*SuperscriptBox[\(5\), \(2\)]\) \ \!\(\*SuperscriptBox[\(11\), \(5\)]\) \!\(\*SuperscriptBox[\(6\), \(3\ \)]\) \!\(\*SuperscriptBox[\(1\), \(2\)]\)", 2, 5}, {93, 17, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(2\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 2}, {101, 17, "\!\(\*SuperscriptBox[\(1\), \(2\)]\) \!\(\*SuperscriptBox[\(3\), \ \(1\)]\) \!\(\*SuperscriptBox[\(5\), \(2\)]\) \ \!\(\*SuperscriptBox[\(11\), \(6\)]\) \!\(\*SuperscriptBox[\(6\), \(3\ \)]\) \!\(\*SuperscriptBox[\(1\), \(2\)]\)", 2, 6}, {108, 18, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(3\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 3}, {112, 18, "\!\(\*SuperscriptBox[\(1\), \(2\)]\) \!\(\*SuperscriptBox[\(3\), \ \(1\)]\) \!\(\*SuperscriptBox[\(5\), \(2\)]\) \ \!\(\*SuperscriptBox[\(11\), \(7\)]\) \!\(\*SuperscriptBox[\(6\), \(3\ \)]\) \!\(\*SuperscriptBox[\(1\), \(2\)]\)", 2, 7}, {123, 19, "\!\(\*SuperscriptBox[\(1\), \(2\)]\) \!\(\*SuperscriptBox[\(3\), \ \(1\)]\) \!\(\*SuperscriptBox[\(5\), \(2\)]\) \ \!\(\*SuperscriptBox[\(11\), \(8\)]\) \!\(\*SuperscriptBox[\(6\), \(3\ \)]\) \!\(\*SuperscriptBox[\(1\), \(2\)]\)", 2, 8}, {123, 19, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(4\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 4}, {138, 20, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(5\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 5}, {153, 21, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(6\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 6}, {168, 22, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(7\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 7}, {183, 23, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(8\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 8}, {198, 24, "\!\(\*SuperscriptBox[\(1\), \(3\)]\) \!\(\*SuperscriptBox[\(4\), \ \(1\)]\) \!\(\*SuperscriptBox[\(7\), \(3\)]\) \ \!\(\*SuperscriptBox[\(15\), \(9\)]\) \!\(\*SuperscriptBox[\(8\), \(4\ \)]\) \!\(\*SuperscriptBox[\(1\), \(3\)]\)", 3, 9}, {213, 25, "\!\(\*SuperscriptBox[\(1\), \(4\)]\) \!\(\*SuperscriptBox[\(5\), \ \(1\)]\) \!\(\*SuperscriptBox[\(9\), \(4\)]\) \ \!\(\*SuperscriptBox[\(19\), \(6\)]\) \!\(\*SuperscriptBox[\(10\), \ \(5\)]\) \!\(\*SuperscriptBox[\(1\), \(4\)]\)", 4, 6}}]

Next is the length-58 optimal ruler showing that . Using brute force, is provable. In 2011, Peter Luschny conjectured that the optimal ruler is the largest optimal ruler that does not use Wichmann’s recipe.

&#10005 Text@Grid[Transpose[{{"split", "diff", "ruler", "\!\(\* StyleBox[SubscriptBox[\"M\", \"n\"],\nFontSlant->\"Italic\"]\)"}, {#, SplitToDiff[#], SplitToRuler[#], Length[SplitToRuler[#]]} &@sparsedata[[58]]}], Frame -> All]

In 2014, Arch D. Robison wrote “Parallel Computation of Sparse Rulers,” where months of computer time was spent on 256 Intel cores to calculate 106,535 sparse rulers up to length 213. Part of this run proved the existence of a length-135 nonperfect ruler.

So while we have identified all the sparse rulers up to length 213, we only have candidates beyond length 213. For the rest of this blog post, “conjectured sparse ruler” means a complete ruler with length greater than 213 and the minimal known number of marks. Above length 213, no sparse rulers have been proven minimal. Length 214 has the first conjectured sparse ruler:

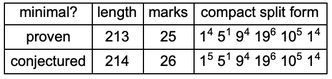
&#10005 Text@Grid[{{"minimal?", "length", "marks", "compact split form"}, {"proven", 213, 25, "\!\(\*SuperscriptBox[\(1\), \(4\)]\) \!\(\*SuperscriptBox[\(5\), \ \(1\)]\) \!\(\*SuperscriptBox[\(9\), \(4\)]\) \ \!\(\*SuperscriptBox[\(19\), \(6\)]\) \!\(\*SuperscriptBox[\(10\), \ \(5\)]\) \!\(\*SuperscriptBox[\(1\), \(4\)]\)"}, {"conjectured", 214, 26, "\!\(\*SuperscriptBox[\(1\), \(5\)]\) \ \!\(\*SuperscriptBox[\(5\), \(1\)]\) \!\(\*SuperscriptBox[\(9\), \ \(4\)]\) \!\(\*SuperscriptBox[\(19\), \(6\)]\) \ \!\(\*SuperscriptBox[\(10\), \(5\)]\) \!\(\*SuperscriptBox[\(1\), \(4\ \)]\)"}}, Frame -> All]

Robison’s run required 1.5 computer years to verify . Computationally verifying would require 3 computer years using current methods. Adding a single mark doubles the computational difficulty of verifying minimality with currently known methods.

You may have heard of sparse rulers, Golomb rulers and difference sets. How do these relate to each other?

• In a sparse ruler, all differences must be covered, but they can be repeated.
• In a Golomb ruler, differences can be missed, but none can be repeated.
• In a difference set, all modular distances must be covered, and none can be repeated.
• In 1967, Robinson and Bernstein predicted the best 24-mark Golomb ruler.
• In 1984, Atkinson and Hassenklover made predictions of the best Golomb rulers with under 100 marks.
• In 2014, distributed.net proved that the predicted Golomb rulers with 24 to 27 marks were indeed correct using thousands of years of computer time. The Robison run verified that predicted behavior for optimal rulers was correct up to 25 marks.
• In 2016, Rokicki and Dogon made predictions of the best Golomb rulers with under 40000 marks.

New Discoveries

In 2019, I devised a formula that expresses the excess of a complete ruler in terms of the length and the number of minimal marks ; here, is the rounding function:

.

For the first 50 lengths, . Then , so .

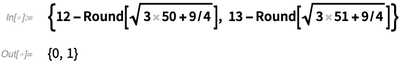
&#10005 {12 - Round[Sqrt[3 50 + 9/4]], 13 - Round[Sqrt[3 51 + 9/4]]}

The excess formula produces the exact number of minimal marks for sparse rulers up to length 213, with two lines of code. In the On-Line Encyclopedia of Integer Sequences (OEIS), this list of the number of minimal marks for a sparse ruler is sequence A046693:

&#10005 A308766[n_] := If[MemberQ[{51, 59, 69, 113, 124, 125, 135, 136, 139, 149, 150, 151, 164, 165, 166, 179, 180, 181, 195, 196, 199, 209, 210, 211}, n], 1, 0]; A046693 = Table[Round[Sqrt[3 n + 9/4]] + A308766[n], {n, 213}]

Based on the sparse rulers and conjectured sparse rulers to length 2020, the excess seems to be a chaotic sequence of 0s and 1s:

&#10005 ListPlot[Take[rulerexcess, 2020], Joined -> True, AspectRatio -> 1/30, Axes -> False, ImageSize -> 520]

If Luschny’s conjecture is correct, then the lowest possible excess is 0 and all conjectured sparse rulers are minimal.

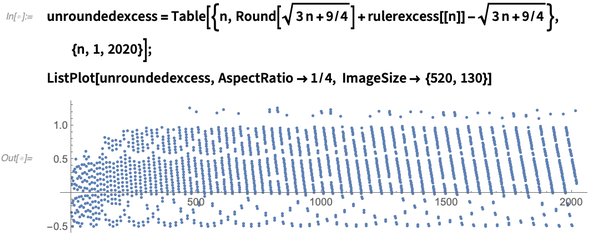
Without rounding, a plot of the best-known number of minimal marks minus shows some distinct patterns up to length 2020. Some points, such as seem to float above and break the pattern, which makes their minimality questionable:

&#10005 unroundedexcess = Table[{n, Round[Sqrt[3 n + 9/4]] + rulerexcess[[n]] - Sqrt[3 n + 9/4]}, {n, 1, 2020}]; ListPlot[unroundedexcess, AspectRatio -> 1/4, ImageSize -> {520, 130}]

Here are lengths of currently conjectured sparse rulers that break the pattern:

&#10005 First /@ Select[unroundedexcess, #[[2]] > 1 &]

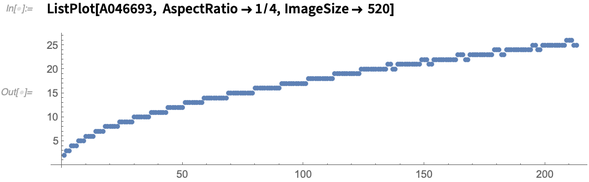
Here is a plot of the verified number of minimal marks to :

&#10005 ListPlot[A046693, AspectRatio -> 1/4, ImageSize -> 520]

Robison discovered that the sequence is not strictly increasing, as seen by the dips. Where do these dips occur?

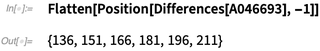
&#10005 Flatten[Position[Differences[A046693], -1]]

How are they spaced?

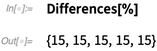
&#10005 Differences[%]

In the previous table, the last six listed Wichmann rulers had these lengths:

&#10005 {138, 153, 168, 183, 198, 213};

These coincide with the positions of the dips:

&#10005 {136, 151, 166, 181, 196, 211} + 2

We can plot and compare Leech’s bounds for the number of minimal marks to the actual number of minimal marks:

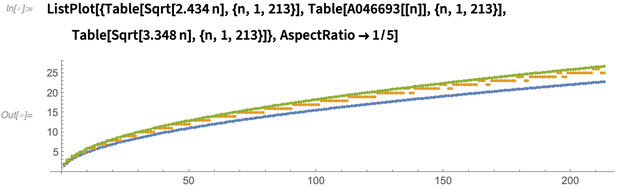
&#10005 ListPlot[{Table[Sqrt[2.434 n], {n, 1, 213}], Table[A046693[[n]], {n, 1, 213}], Table[Sqrt[3.348 n], {n, 1, 213}]}, AspectRatio -> 1/5]

The furthest values in the lines of dots are almost always lengths of optimal Wichmann rulers, with the last known exception being . We saw that some of the lengths of optimal Wichmann rulers were . Let us call these Wichmann values. These lengths (A289761) are given by:

&#10005 WichmannValues = Table[(n^2 - (Mod[n, 6] - 3)^2)/3 + n, {n, 1, 24}]

Here I arrange numbers to 213 so that the bottom of each column is a Wichmann value. Under the blue line is the number of marks associated with the column. This is a numeric representation of the excess pattern:

values are gray.

 values are bold black.

&#10005 Grid[Append[ Transpose[Table[PadLeft[Take[Style[If[rulerexcess[[#]] == 1, Style[#, Black, Bold, 16], Style[#, Gray, 14]]] & /@ Range[213], {WichmannValues[[n]] + 1, WichmannValues[[n + 1]]}], 15, ""], {n, 24 - 1}]], Range[3, 25]], Spacings -> {.2, .2}, Dividers -> {False, -2 -> Blue}]

For convenience, I’ll use various terms relating to the excess pattern:

• A column is a column in the excess pattern
• is the column for rulers with marks
• The height is the placement within a column; Wichmann values have height 0
• The rise is the number of entries in a column; has 15 entries
• The excess coordinate is for length within the excess pattern
• The excess fraction (a normalized form) is for length
• A window is a contiguous set of rulers within a column
• A mullion is a contiguous set of rulers within a column (a space between windows is a mullion)

A few sample values for rulers in columns 19 and 25:

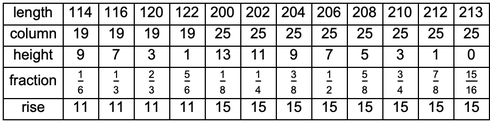
&#10005 Text@Grid[ Transpose[ Prepend[Flatten[{#, ExcessCoordinates[#]}] & /@ {114, 116, 120, 122, 200, 202, 204, 206, 208, 210, 212, 213}, {"length", "column", "height", "fraction", "rise"}]], Frame -> All]

Here is the excess pattern of the best-known excess values for lengths up to 10501. is gray, is black. This is a pixel representation of the excess pattern:

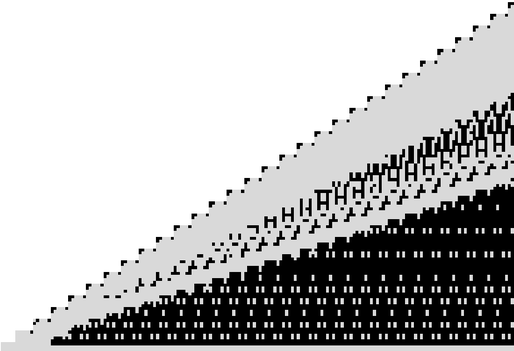
&#10005 ArrayPlot[Transpose[Table[ PadLeft[ First /@ Take[Transpose[{Take[rulerexcess, 10501], Range[10501]}], {WichmannValues[[n]] + 1, WichmannValues[[n + 1]]}], 119, 2], {n, 1, 175}]], ColorRules -> {0 -> LightGray, 1 -> Black, 2 -> White}, PixelConstrained -> 3, Frame -> False]

The creator of OEIS, N. J. A. Sloane, describes this pattern as “Dark Satanic Mills on a Cloudy Day.” This unique description refers to the solid black part of the pattern with many windows, dark mills and the irregular patches above, the clouds.

We calculate these coordinates for various lengths:

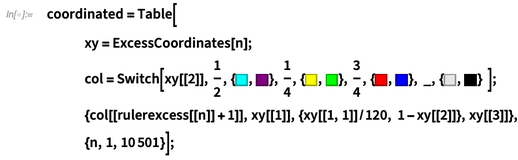
&#10005 coordinated = Table[ xy = ExcessCoordinates[n]; col = Switch[xy[[2]], 1/ 2, {RGBColor[0, 1, 1], RGBColor[0.5, 0, 0.5]}, 1/ 4, {RGBColor[1, 1, 0], RGBColor[0, 1, 0]}, 3/ 4, {RGBColor[1, 0, 0], RGBColor[0, 0, 1]}, _, {GrayLevel[0.9], GrayLevel[0]} ]; {col[[rulerexcess[[n]] + 1]], xy[[1]], {xy[[1, 1]]/120, 1 - xy[[2]]}, xy[[3]]}, {n, 1, 10501}];

Here is the excess pattern of the best-known excess values for lengths up to 10501.
.
Some colors have exact excess fractions: :

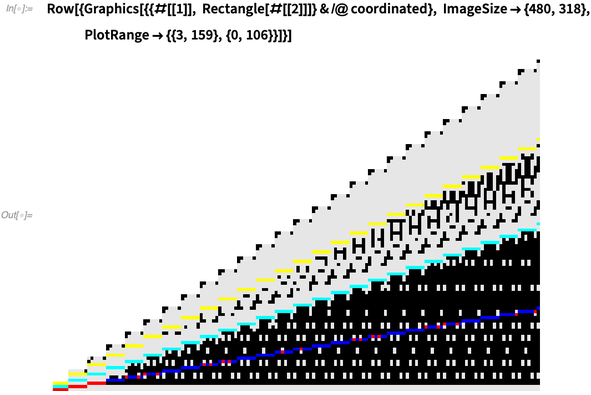
&#10005 Row[{Graphics[{{#[[1]], Rectangle[#[[2]]]} & /@ coordinated}, ImageSize -> {480, 318}, PlotRange -> {{3, 159}, {0, 106}}]}]

This plots the excess fractions. The excess fractions , and occur in each column; they are the colored horizontal lines:

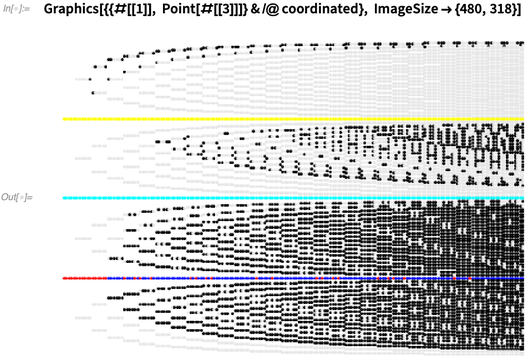
&#10005 Graphics[{{#[[1]], Point[#[[3]]]} & /@ coordinated}, ImageSize -> {480, 318}]

Here’s a version of the excess pattern where the excess fraction 1/2 makes a horizontal line. A crushed version of the normalized excess fraction pattern is shown on the right.

Some colors have exact excess fractions as before: :

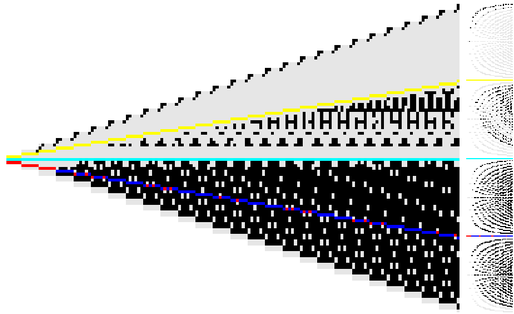
&#10005 Row[{Graphics[{{#[[1]], Rectangle[#[[2]] + {0, 53 - Round[#[[4]]/2]}]} & /@ coordinated}, ImageSize -> {480, 318}, PlotRange -> {{3, 159}, {0, 106}}], Graphics[{AbsolutePointSize[.1], {#[[1]], Point[#[[3]]/{10, 1}]} & /@ coordinated}, ImageSize -> {Automatic, 320}]}]

For the following diagram, on the left are columns C₆₈ to C₇₃ with cells representing lengths 1516 to 1797.

On the right is the normalized excess fraction:

&#10005 farey = Select[FareySequence[24], MemberQ[{1, 2, 3, 4, 6, 8, 12, 24}, Denominator[#]] &]; took = Take[coordinated, 8479]; Row[{Graphics[{EdgeForm[Black], Table[ Tooltip[{coordinated[[k, 1]], Rectangle[coordinated[[k, 2]]]}, {k, coordinated[[k, 2]], sparsedata[[k]]}], {k, 1516, 1797}], Arrowheads[Medium], Arrow[{{73, 46} + {5, 1/2}, {73, 46} + {1/2, 1/2}}], Text[Row[{"Top of column ", Subscript[Style["C", Italic], "73"], " with 73 marks, length 1751"}], {73, 46} + {5, 1/2}, {Left, Center}], Arrow[{{73, 0} + {5, 1/2}, {73, 0} + {1/2, 1/2}}], Text[Row[{"Bottom of column ", Subscript[Style["C", Italic], "73"], " with 73 marks, length 1797"}], {73, 0} + {5, 1/2}, {Left, Center}], Arrow[{{71, 17} + {5, 1/2}, {71, 17} + {1/2, 1/2}}], Text[Row[{"Window in column ", Subscript[Style["C", Italic], "71"], ", 1686 and 1687"}], {71, 17} + {5, 1/2}, {Left, Center}], Line[{{73, 24} + {3, 1/2}, {73, 24} + {5, 1/2}}], Arrow[{{73, 24} + {3, 1/2}, {73, 27} + {1/2, 1/2}}], Arrow[{{73, 24} + {3, 1/2}, {73, 21} + {1/2, 1/2}}], Text[Row[{"Window in column ", Subscript[Style["C", Italic], "73"], ", 1770 to 1776"}], {73, 24} + {5, 1/2}, {Left, Center}], Line[{{73, 12} + {3, 1/2}, {73, 12} + {5, 1/2}}], Arrow[{{73, 12} + {3, 1/2}, {73, 20} + {1/2, 1/2}}], Arrow[{{73, 12} + {3, 1/2}, {73, 2} + {1/2, 1/2}}], Text[Row[{"Mullion in column ", Subscript[Style["C", Italic], "73"], ", 1777 to 1795"}], {73, 12} + {5, 1/2}, {Left, Center}] }, ImageSize -> {380, 420}], Graphics[{AbsolutePointSize[.01], {#[[1]], Point[#[[3]]/{10, 1}]} & /@ coordinated, Style[ Text[Row[{Numerator[#], "/", Denominator[#]}], {-.03, 1 - #}], 10] & /@ farey}, AspectRatio -> 4, ImageSize -> {115, 420}]}, Alignment -> {Bottom, Bottom}]

In the normalized excess pattern:

• 0 to 1/4 has mostly excess 0
• 1/4 to 1/2 has a chaotic pattern
• 1/2 to 1 has mostly excess 1

Various sequences from OEIS:


A004137: maximal number of edges in a graceful graph on nodes

A046693: minimal marks for a sparse ruler of length 

A103300: number of perfect rulers with length 

A289761: maximum length of an optimal Wichmann ruler with marks
A308766: lengths of sparse rulers with excess 1
A309407: round(sqrt(3* + 9/4))

A326499: excess of a length- sparse ruler

You can also check out the “Sparse Rulers” Demonstration, which has thousands of these sparse rulers:

Producing two million sparse rulers required over two thousand Wichmann-like rulers, construction recipes that all work with arbitrarily large values. Substituting and values into a Wichmann recipe is computationally easy:

Proof That E ≤ 1

The excess of a length- sparse ruler with minimal number of marks is .

Sparse ruler conjecture: E = 0 or 1 for all sparse rulers.

Part 1, L > 257 992

Finding sparse rulers satisfying for all lengths under 257992 is difficult and likely couldn’t have been done without current-era computers. Finding longer-length sparse rulers turns out to be easy and could have been done back in 1963 with the following simple proof.

is the split form of Wichmann recipe 1, or .

is , , : or in the diff form.

is an extension. A sparse ruler starting with 1s in the diff form can be extended by up to 1s with an extra mark at the end. This new ruler looks like . The new lengths above are handled by differences , and . Note that is not a sparse ruler since the length cannot be expressed as a difference.

The “Wichmann Columns” Demonstration generates a column in the excess pattern by using only sparse rulers made by the first two Wichmann recipes, W₁ and W₂, and extensions of these rulers.

indicates that a sparse ruler cannot be generated by W₁, W₂ or by extending them.
indicates a generated sparse ruler with excess 0.
indicates a generated sparse ruler with excess 1.

We can see in the following Manipulate that length cannot be covered by this method in the excess pattern column representing sparse rulers with 236 marks. Adjust the slider or hover over a value to get a Tooltip with the generated sparse ruler:

Red pixels show where extensions don’t solve in the excess pattern:

&#10005 pixels = Table[ Reverse[PadRight[Switch[#[[2]], RGBColor[0, 0, 1], 1, RGBColor[0, Rational[2, 3], 0], 2, RGBColor[1, 0, 0], 3] & /@ Reverse[First /@ WichmannColumn[k][[1, 1, 1]]], 600]], {k, 2, 895}]; ArrayPlot[Transpose[Drop[pixels, 363]], PixelConstrained -> 1, Frame -> False, ColorRules -> {0 -> White, 1 -> LightGray, 2 -> Gray, 3 -> Red}]

Lengths of sparse rulers generated by and are generated by order-2 polynomials differing by 1. The behavior of values generated by these polynomials is completely predictable and ultimately generates two weird sequences: sixsev and sixfiv:

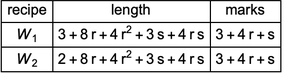
&#10005 Text@Grid[Prepend[{Subscript[Style["W", Italic], #], WichmannLength[WichmannRecipes[[#]]], WichmannMarks[WichmannRecipes[[#]]]} & /@ {1, 2}, {"recipe", "length", "marks"}], Frame -> All]

Sequence sixsev consists of infinite 6s and 7s. Similarly, the sequence sixfiv consists entirely of 6s and 5s:

&#10005 cutoff = 15; (*raise the cutoff to go farther*) sixsev = Drop[ Flatten[Table[Table[{Table[6, {n}], 7}, {6}], {n, 0, cutoff}]], 1]; sixfiv = Drop[ Flatten[Table[Table[{Table[6, {n}], 5}, {6}], {n, 0, cutoff}]], 2];

&#10005 Column[{Take[sixsev, 80], Take[sixfiv, 80]}]

What are the values for the and recipe in column 236 with ? What are the Wichmann recipe column zeros (WRCZ)? Code for WRCZ, based on sixsev and sixfiv, is shown in the initialization section in the downloadable notebook. Column 236 in the excess pattern has seven sets of values. The height of a column is roughly (2/3)*column, 159 in this case. The average possible extension is roughly a quarter of the column height:

&#10005 WRCZ[236]

In the excess pattern, each column divides into quarter sections with the same size as the extension lengths of and . If we can show that eventually there are at least four reasonably spaced and zeros in each column, we’re done:

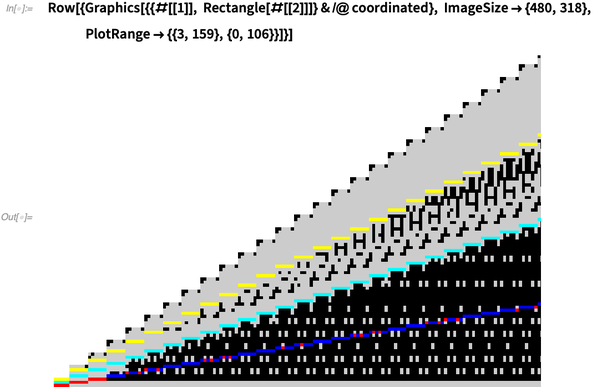
&#10005 Row[{Graphics[{{#[[1]], Rectangle[#[[2]]]} & /@ coordinated}, ImageSize -> {480, 318}, PlotRange -> {{3, 159}, {0, 106}}]}]

The last column in the excess pattern without four reasonably spaced and zeros is column 880:

&#10005 WRCZ[880]

Here are the lengths generated by these pairs:

&#10005 zero880 = (3 + 8 r + 4 r^2 + 3 s + 4 r s) /. {r -> #[[1]], s -> #[[2]]} & /@ WRCZ[880]

Notice how the generated lengths for this column are palindromic, a worst-case scenario. Length 257992 isn’t covered by the zeros here and is out of reach of the last zero in the previous column, .

The acceleration of change between values generated by is a constant –24. The spacing between zeros is predictable:

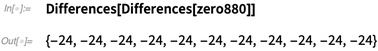
&#10005 Differences[Differences[zero880]]

Only four reasonably spaced zeros are needed per column. The polynomial inexorably offers more and more zeros. Column 880 is the last column where extensions can fail:

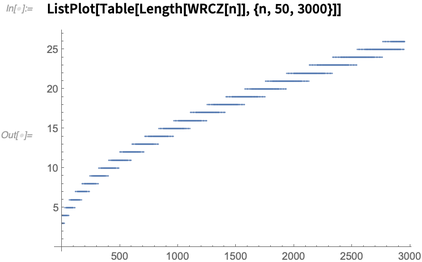
&#10005 ListPlot[Table[Length[WRCZ[n]], {n, 50, 3000}]]

Another plot showing that extensions overwhelm the differences:

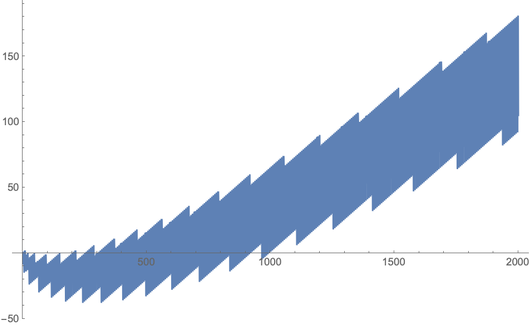
&#10005 ListPlot[Table[(WRCZ[k][[1, 1]] + 2) - Max[ Differences[ Union[3 + 8 r + 4 r^2 + 3 s + 4 r s /. Thread[{r, s} -> #] & /@ WRCZ[k]]]] , {k, 50, 2050}], Joined -> True]

All integer lengths greater than 257992 (corresponding to 880 marks) are excess-01 rulers made by extensions to Wichmann recipe 1.

All integer lengths greater than 119206 (corresponding to 598 marks) are excess-01 rulers made by extensions and double extensions to Wichmann recipe 1. Here’s an example double extension that covers length 257992:

&#10005 SplitExtensions[ Last[SplitExtensions[ WichmannRuler[WichmannRecipes[[1]], {146, 292}]]]][[6]]

&#10005 Dot @@ %

Part 2, L ≤ 257 992

We can programmatically verify the conjecture with precalculated rulers to length 2020, or to length 257992 with more running time. This tallies the number of 0s and 1s for the excess, up to length 2020:

&#10005 Tally[Sparseness[SplitToRuler[#]] & /@ Take[sparsedata, 2020]]

I knew Robison found rulers to length 213, so I wanted to show samples. But except for the counts, all the ruler data was lost. I rebuilt it, but without access to the Intel superclusters. This search started with trying to make an image showing a row of column-presented sparse rulers from length 1 to length 213.

First, here are sparse rulers up to length 36 with the mark positions converted into pixel positions. The gray rows indicate that the sparse ruler for that length is unique:

&#10005 Row[{Style[ Column[Table[SplitToRuler[sparsedata[[n]]], {n, 1, 36}], Alignment -> Right], 8], ArrayPlot[Table[PadRight[ReplacePart[Table[0, {n + 1}], ({# + 1} & /@ SplitToRuler[sparsedata[[n]]]) -> 1], 37] + If[counts[[n]] == 1, 2, 0], {n, 1, 36}], PixelConstrained -> 11, ColorRules -> {0 -> White, 1 -> Black, 2 -> GrayLevel[.9], 3 -> Black }, Frame -> False]}]

The following plot is a transpose of the previous plot, extended to a length of 213. Each column represents a sparse ruler, with gray columns indicating uniqueness. These columns line up with the log plot after the next paragraph:

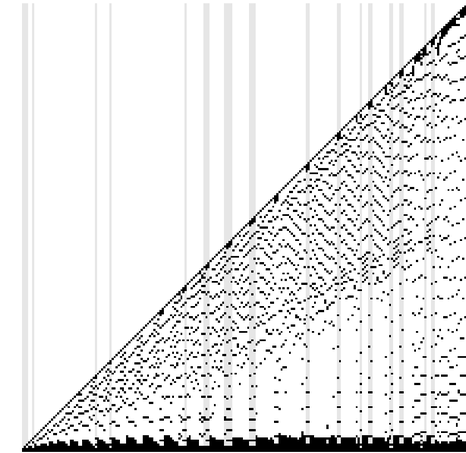
&#10005 Row[{Spacer[20], ArrayPlot[ Transpose[Reverse /@ Table[PadRight[ReplacePart[Table[0, {n + 1}], ({# + 1} & /@ SplitToRuler[sparsedata[[n]]]) -> 1], 215] + If[counts[[n]] == 1, 2, 0], {n, 1, 213}]], PixelConstrained -> 2, ColorRules -> {0 -> White, 1 -> Black, 2 -> GrayLevel[.9], 3 -> Black }, Frame -> False]}]

And here is a log plot of the number of distinct sparse rulers of length to length 213, which shows that there are usually fewer (blue) rulers and more (brown) rulers. Points on the bottom correspond to unique rulers (and a gray column in the previous image):

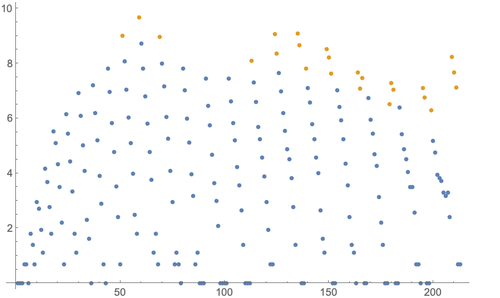
&#10005 ListPlot[Take[#, 2] & /@ # & /@ GatherBy[Transpose[{Range[213], Log /@ Take[counts, 213], Take[rulerexcess, 213]}], Last], ImageSize -> 450]

Length has 15990 distinct sparse rulers. These counts are sequence A103300. Out of the first 213 lengths, 31 of them have a unique sparse ruler. I suspect many lengths above 213 have unique or hard-to-find minimal representations.

The following log plot shows the number of distinct sparse rulers and conjectured sparse rulers of length to length 10501, found in the search that produced 2,016,735 sparse rulers and conjectured sparse rulers:

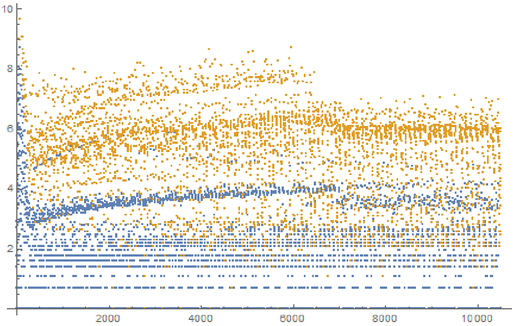
&#10005 ListPlot[Take[#, 2] & /@ # & /@ GatherBy[Transpose[{Range[10501], Log /@ Take[counts, 10501], Take[rulerexcess, 10501]}], Last]]

In the downloadable notebook I show many ways to use a sparse ruler to generate new sparse rulers, which can in turn make more sparse rulers. I call this process recursion. Processing shorter-length rulers gave better results and needed less time, so rulers of a length above 4000 were initially not used to produce more rulers. After cracking the particularly hard length 1792, I extended the new ruler processing to length 7000 in hopes of finding an example of length 5657. After checking to 10501, I temporarily stopped the search.

Various regularities and patterns can be seen, but part of the change in pattern is due to arbitrary cutoffs in processing at 4000 and 7000. One curious case is , with 363 rulers. Nearby is , with 3619 rulers. If an sparse ruler exists, the first clue will likely be an length with an unusually high count of examples.

An infinite number of complete rulers with can be made using all 2069 Wichmann-like recipes. How well does the catalog of Wichmann recipes work? To find out, I tried the following overnight run:

&#10005 addedrulers=Table[With[{wich=FindWichmann[hh][[1,1]]}, WichmannRuler[WichmannRecipes[[wich[[1]]]], wich[[3]]]], {hh,10520,17553}]

How do these 7033 new complete rulers match up with the pattern? About 6448 rulers match the previous pattern well. About 587 rulers appear to be violations:

&#10005 ArrayPlot[ Transpose[Drop[Table[PadLeft[Take[Take[oldrulerexcess, 17553], {WichmannValues[[n]] + 1, WichmannValues[[n + 1]]}], 151, 6], {n, 1, 227}], 92]], ColorRules -> {0 -> LightGray, 1 -> Black, 6 -> White, 2 -> Green, 3 -> Brown, 4 -> Red, 5 -> Yellow }, PixelConstrained -> 4, Frame -> False]

Adding an extension is the simplest way to make new complete rulers. Let us try that. This code (which will also require a long running time) finds 586 lengths that can be improved this simple way:

&#10005 oldsparsedata=CloudGet["https://wolfr.am/KeKbjOBs"]; rulerexcess = oldrulerexcess; newrulers = First /@ SplitBy[ Sort[{Last[#], Length[#], RulerToSplit[#]} & /@ Complement[Union[SparseCheckImprove /@ Flatten[ Table[With[{ruler = SplitToRuler[#]}, Append[ruler, Last[ruler] + n]], {n, 1, 40}] & /@ Drop[oldsparsedata, 10501], 1]], {False}]], First]; Do[length = newrulers[[index, 1]]; rulerexcess[[length]] = newrulers[[index, 2]] - Round[Sqrt[3 length + 9/4]]; sparsedata[[length]] = newrulers[[index, 3]], {index, 1, Length[newrulers]}];

After that trial, a single exception to the sparse ruler conjecture remains in this range, at . The pattern cleaned up nicely:

&#10005 ArrayPlot[ Transpose[ Drop[Table[ PadLeft[Take[ReplacePart[Take[rulerexcess, 17553], 16617 -> 2], {WichmannValues[[n]] + 1, WichmannValues[[n + 1]]}], 151, 6], {n, 1, 227}], 92]], ColorRules -> {0 -> LightGray, 1 -> Black, 6 -> White, 2 -> Green, 3 -> Brown, 4 -> Red, 5 -> Yellow }, PixelConstrained -> 4, Frame -> False]

I did not expect this trial to work so well.

I had to find an example for . The tools in this notebook gave me an example in a few hours. The sparse ruler conjecture is true to at least 17553:

&#10005 sparse16617 = {{1, 75, 1, 75, 149, 74, 42, 1, 19, 1}, {32, 1, 4, 37, 73, 37, 1, 32, 2, 4}}; temp = SplitToRuler[sparse16617]; {Last[temp], Length[temp], Sparseness[temp]}

Length 16617 is the final difficult value for . All lengths 16618 to 257992 can be solved with the 2069 known Wichmann recipes or extensions.

After the initialization section in the notebook is ReasonableRuler, which will find a ruler with excess 0 or 1 for any given positive integer length. Here’s a ruler for length 100000:

&#10005 ReasonableRuler[100000]

The function generates example sparse rulers with E = 0 or 1 for all lengths up to 257992 within a few minutes.

QED.

Conjectures and Wrap-Up

The Leech bounds can be improved. The Leech upper and lower bounds drift far away from the best-known values for minimal marks :

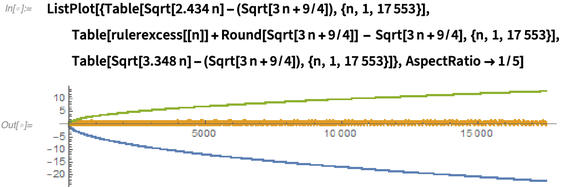
&#10005 ListPlot[{Table[Sqrt[2.434 n] - (Sqrt[3 n + 9/4]), {n, 1, 17553}], Table[rulerexcess[[n]] + Round[Sqrt[3 n + 9/4]] - Sqrt[3 n + 9/4], {n, 1, 17553}], Table[Sqrt[3.348 n] - (Sqrt[3 n + 9/4]), {n, 1, 17553}]}, AspectRatio -> 1/5]

I know of 11 rulers with the following properties:

1. and complete

2. Length greater than 213

3. Excess fraction ≥ 4/7

4. Not built with a Wichmann recipe

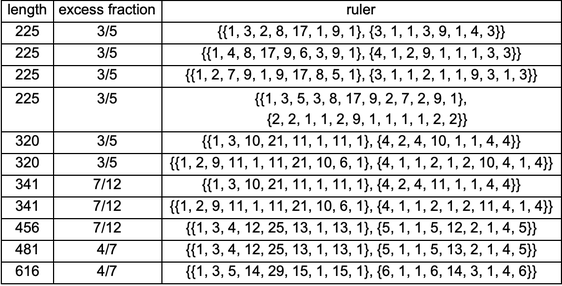
&#10005 highzero = {{{1, 3, 2, 8, 17, 1, 9, 1}, {3, 1, 1, 3, 9, 1, 4, 3}}, {{1, 4, 8, 17, 9, 6, 3, 9, 1}, {4, 1, 2, 9, 1, 1, 1, 3, 3}}, {{1, 2, 7, 9, 1, 9, 17, 8, 5, 1}, {3, 1, 1, 2, 1, 1, 9, 3, 1, 3}}, {{1, 3, 5, 3, 8, 17, 9, 2, 7, 2, 9, 1}, {2, 2, 1, 1, 2, 9, 1, 1, 1, 1, 2, 2}}, {{1, 3, 10, 21, 11, 1, 11, 1}, {4, 2, 4, 10, 1, 1, 4, 4}}, {{1, 2, 9, 11, 1, 11, 21, 10, 6, 1}, {4, 1, 1, 2, 1, 2, 10, 4, 1, 4}}, {{1, 3, 10, 21, 11, 1, 11, 1}, {4, 2, 4, 11, 1, 1, 4, 4}}, {{1, 2, 9, 11, 1, 11, 21, 10, 6, 1}, {4, 1, 1, 2, 1, 2, 11, 4, 1, 4}}, {{1, 3, 4, 12, 25, 13, 1, 13, 1}, {5, 1, 1, 5, 12, 2, 1, 4, 5}}, {{1, 3, 4, 12, 25, 13, 1, 13, 1}, {5, 1, 1, 5, 13, 2, 1, 4, 5}}, {{1, 3, 5, 14, 29, 15, 1, 15, 1}, {6, 1, 1, 6, 14, 3, 1, 4, 6}}}; Text@Grid[Prepend[{Dot @@ #, Row[{ToString[Numerator[#]], "/", ToString[Denominator[#]]}] &@ ExcessCoordinates[Dot @@ #][[2]], #} & /@ highzero, {"length", "excess fraction", "ruler"}], Frame -> All]

Conjectures

1. Peter Luschny’s optimal ruler conjecture is true; is the last non-Wichmann optimal sparse ruler

2. The lower bound for is 

3. The list of 11 rulers immediately above is complete

I’ve shown how approaching the problem computationally with the Wolfram Language can help not only to solve but also construct a proof for the sparse rulers problem that has historically fascinated so many. Make your own mark—to continue exploring, be sure to download this post’s notebook, which features lots of additional code, the connection between sparse rulers and graceful graphs, and a longer discussion for finding sparse rulers. Can any of the current excess values be improved? Are there more excellent Wichmann-like recipes? I would love to know—submit your recipes in the comments or to Wolfram Community!

Many thanks to T. Sirgedas, A. Robison, G. Beck and N. J. A. Sloane for help with this search.

References

Leech, J. “On the Representation of 1, 2, …, n by Differences.” Journal of the London Mathematical
  Society s1–31.2 (1956): 160–169.

Luschny, P. “The Optimal Ruler Conjecture.” The On-Line Encyclopedia of Integer Sequences.

Pegg, E. “Sparse Ruler Conjecture.” Wolfram Community.

Rédei, L. and A. Rényi. “On the Representation of the Numbers 1, 2, …, n by Means of Differences.”
  Matematicheskii Sbornik 24(66), no. 3 (1949): 385–389.

Robison, A. D. “Parallel Computation of Sparse Rulers.” Intel Developer Zone.

Rokicki, T. and G. Dogon. “Golomb Rulers: Pushing the Limits.” cube20.org.

Wichmann, B. “A Note on Restricted Difference Bases.” Journal of the London Mathematical Society
  s1–38.1 (1963): 465–466. doi:10.1112/jlms/s1-38.1.465.

Wikipedia Contributors. “Sparse Ruler.” Wikipedia, the Free Encyclopedia.