The Data Science of MathOverflow
New Archive Conversion Utility in Version 12
Soon there will be 100,000 questions on MathOverflow.net, a question-and-answer site for professional mathematicians! To celebrate this event, I have been working on a Wolfram Language utility package to convert archives of Stack Exchange network websites into Wolfram Language entity stores.
The archives are hosted on the Internet Archive and are updated every few months. The package, although not yet publicly available, will be released in the coming weeks as part of Version 12 of the Wolfram Language—so keep watching this space for more news about the release!
Although some data analysis can be done with tools such as the Stack Exchange Data Explorer, queries are usually limited in size or computation time, as well as to text-only formats. Additionally, they require some knowledge of SQL. But with a local copy of the data, much more can be done, including images, plots and graphs.
With the utility package operating on a local archive, it’s easy to perform much deeper data analysis using all of the built-in tools in the Wolfram Language. In particular, Version 12 of the Wolfram Language adds support for RDF and SPARQL queries, as well as useful constructs such as FilteredEntityClass and SortedEntityClass.
For professional mathematicians who already use Mathematica and the Wolfram Language, this utility allows for seamless investigation into the data on MathOverflow.net or any Stack Exchange network site. Feel free to follow along with me as I do some of this investigation by running the code in a notebook, or just sit back and enjoy the ride as we explore MathOverflow.net with the Wolfram Language!
Importing a MathOverflow EntityStore
The entity stores created by the utility package allow for quick access to the data in a format that’s easy for Wolfram Language processing, such as queries using the Entity framework, machine learning functionality, visualization, etc.
Let’s start by downloading a pre-generated EntityStore from the Wolfram Cloud to the notebook’s directory:
 Engage with the code in this post by downloading the Wolfram Notebook
Engage with the code in this post by downloading the Wolfram Notebook

✕
downloadedFile=URLDownload[CloudObject["StackExchange2EntityStore/mathoverflow.net.mx"],NotebookDirectory[]] |
Import the EntityStore from the downloaded file:
|
✕
store=Import[downloadedFile]; |
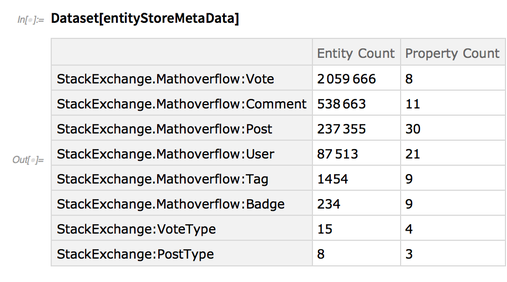
The store is quite large, consisting of nearly three million entities in several entity types:

✕
entityStoreMetaData=AssociationMap[<|"Entity Count"->Length[store[#,"Entities"]],"Property Count"->Length[store[#,"Properties"]]|>&,store[]]//ReverseSortBy[Lookup["Entity Count"]]; |
✕
Dataset[entityStoreMetaData] |
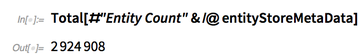
✕
Total[#"Entity Count"&/@entityStoreMetaData] |
Lastly, we need to register the EntityStore for use in the current session:
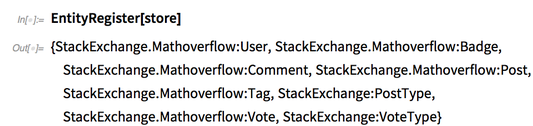
This returns a list of all of the new entity types from the EntityStore that are now available through EntityValue (you can access them by registering the EntityStore via EntityRegister).
For those who are familiar with the Stack Exchange network, these types may be very familiar. But for those who are not, or if you just need a refresher, here’s a basic rundown of a few of the different types:
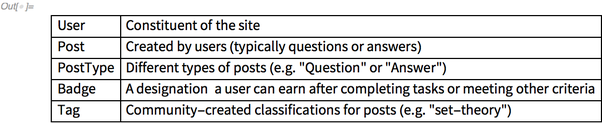
The remaining types not listed are beyond the scope of my post, but you can learn more about them in the README on the archives, or by visiting the frequently asked questions on any Stack Exchange network site.
Accessing MathOverflow.net Posts
Now that the EntityStore is loaded, we can access it through the Entity framework.
Let’s look at some random posts:

✕
RandomEntity["StackExchange.Mathoverflow:Post",3] |
The “Post” entities are formatted with the post type (Q for question, A for answer), the user who authored the post in square brackets, a short snippet of the post and a hyperlink (the blue ») to the original post on the web.
Many of the other entity types format similarly—this is to give proper context, allow for manual exploration on the site itself and give attribution to the original authors (they created the content on the site, after all).
Taking just one of these posts, we can find a lot of information about it with a property association:

✕
Entity["StackExchange.Mathoverflow:Post", "272527"][{accepted answer,answer count,body,closed date,comment count,comments,community owned date,creation date,duplicate posts,favorite count,id,last activity date,last edit date,last editor,linked posts,owner,post type,score,tags,title,URL,view count},"PropertyAssociation"]
|
For example, one may be interested in the posts for a given tag, such as set theory.
We can find how many set theory questions have been asked:
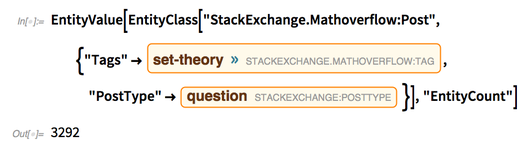
✕
EntityValue[EntityClass["StackExchange.Mathoverflow:Post",{"Tags"->Entity["StackExchange.Mathoverflow:Tag", "SetTheory"],"PostType"->Entity["StackExchange:PostType", "1"] }],"EntityCount"]
|
We can even see the intersections of different tags, such as set theory and plane geometry:

✕
EntityValue[EntityClass["StackExchange.Mathoverflow:Post",{"Tags"->ContainsAll[{Entity["StackExchange.Mathoverflow:Tag", "SetTheory"],Entity["StackExchange.Mathoverflow:Tag", "PlaneGeometry"]}],"PostType"->Entity["StackExchange:PostType", "1"] }],"Entities"]
|
It’s important to note that as of this writing, the archives have not been updated to include the 100,000th question, so we can see that there are only 98,165 questions as of December 2, 2018:

✕
EntityClass["StackExchange.Mathoverflow:Post","PostType"->Entity["StackExchange:PostType", "1"]]["EntityCount"] |

✕
EntityValue[Entity["StackExchange.Mathoverflow:Post"],"LastPostTime"] |
Of course, there is a seemingly endless number of queries one can make on this dataset.
A few ideas that I had were to find and analyze:
- The distribution of post scores (specifically the (nearly) 100k questions)
- Word distributions and frequencies (e.g.
 -grams)
-grams) - “Post Thread” networks
![]() snippets (
snippets (![]() being the language frequently used on Stack Exchange to format equations and other relations)
being the language frequently used on Stack Exchange to format equations and other relations)- Mathematical propositions (e.g. theorems, lemmas, axioms) mentioned in posts
- Famous mathematicians and propositions that are named after them
Let’s tackle these one at a time.
Analyzing Posts
Post Score Distributions
Since there are over 237,000 posts on MathOverflow in total, the distribution of their scores must be very large.
Let’s look at this distribution, noting that some post scores can be negative if they are downvoted by users in the community:

✕
allScores=EntityValue["StackExchange.Mathoverflow:Post",EntityProperty["StackExchange.Mathoverflow:Post", "Score"]]; |
|
✕
postScoreDistribution=Tally[allScores]; |
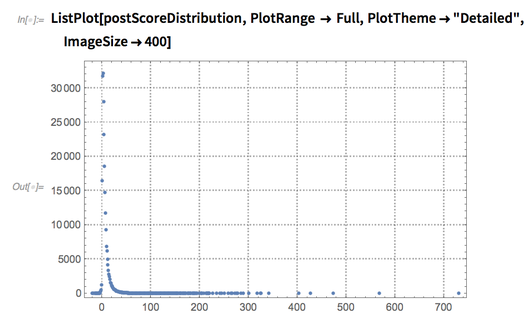
✕
ListPlot[postScoreDistribution,PlotRange -> Full,PlotTheme->"Detailed",ImageSize->400] |
That’s hard to read—it looks better on a log-log scale, and it becomes mostly straight beyond the first several points:
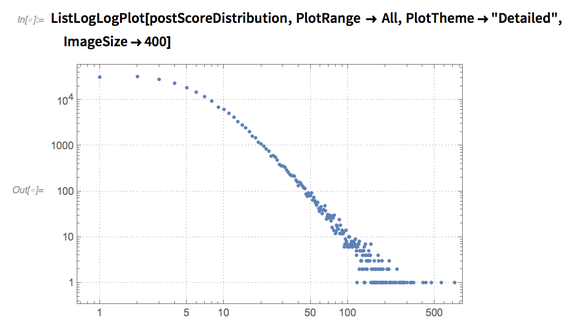
✕
ListLogLogPlot[postScoreDistribution,PlotRange -> All,PlotTheme->"Detailed",ImageSize->400] |
Let’s focus on the positive post scores below 50:

✕
scoresBelowFifty=EntityValue[EntityClass["StackExchange.Mathoverflow:Post","Score"->Between[{1,50}]],"Score"];
|
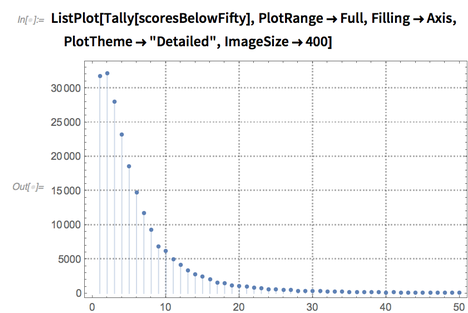
✕
ListPlot[Tally[scoresBelowFifty],PlotRange->Full,Filling->Axis,PlotTheme->"Detailed",ImageSize->400] |
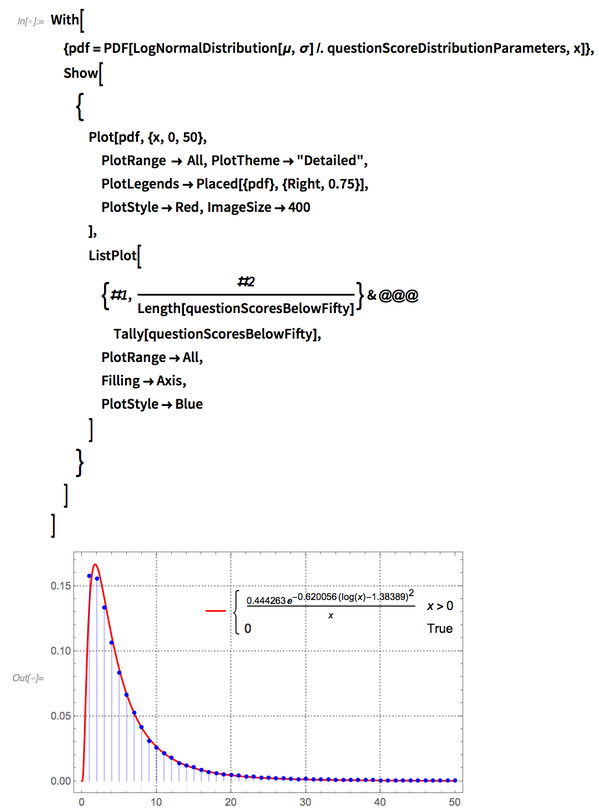
It looks like it might be a log-normal distribution, so let’s find the fitting parameters for it:

✕
distributionParameters=FindDistributionParameters[scoresBelowFifty,LogNormalDistribution[μ,σ]] |
Plotting both on the same (normalized) scale shows they agree quite well:
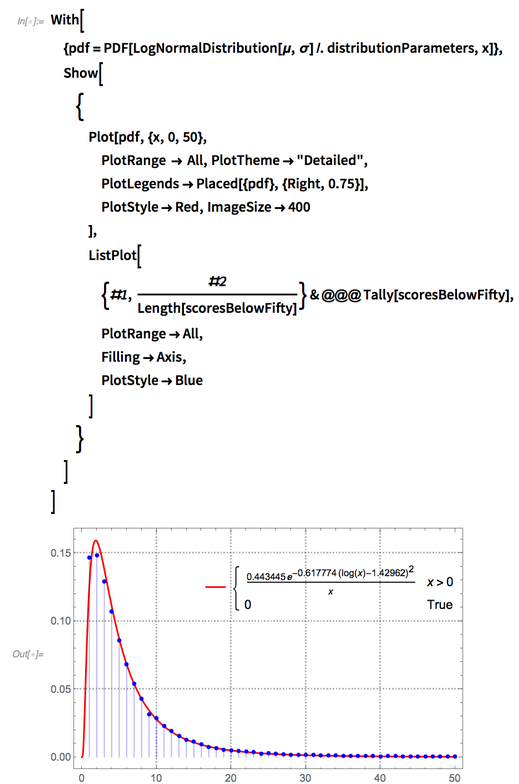
✕
With[
{pdf=PDF[LogNormalDistribution[μ,σ]/.distributionParameters,x]},
Show[
{
Plot[pdf,{x,0,50},
PlotRange -> All,PlotTheme->"Detailed",
PlotLegends->Placed[{pdf},{Right,0.75}],
PlotStyle->Red,ImageSize->400
],
ListPlot[
{#1,#2/Length[scoresBelowFifty]}&@@@Tally[scoresBelowFifty],
PlotRange->All,
Filling->Axis,
PlotStyle->Blue
]
}
]
]
|
We can repeat this analysis on the (almost) 100k questions:
✕
allQuestionScores=EntityValue[EntityClass["StackExchange.Mathoverflow:Post","PostType"->Entity["StackExchange:PostType", "1"]],EntityProperty["StackExchange.Mathoverflow:Post", "Score"]]; |

✕
allQuestionScores//Length |
|
✕
questionScoreDistribution=Tally[allQuestionScores]; |
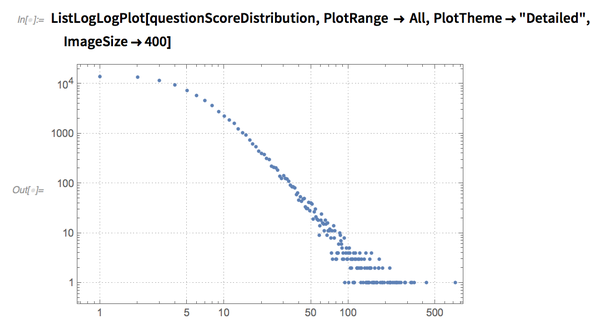
✕
ListLogLogPlot[questionScoreDistribution,PlotRange -> All,PlotTheme->"Detailed",ImageSize->400] |
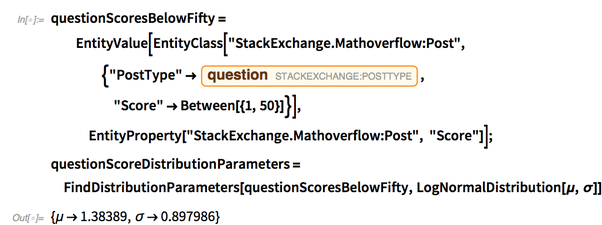
✕
questionScoresBelowFifty=EntityValue[EntityClass["StackExchange.Mathoverflow:Post",{"PostType"->Entity["StackExchange:PostType", "1"],"Score"->Between[{1,50}]}],EntityProperty["StackExchange.Mathoverflow:Post", "Score"]];
questionScoreDistributionParameters=FindDistributionParameters[questionScoresBelowFifty,LogNormalDistribution[μ,σ]]
|
✕
With[
{pdf=PDF[LogNormalDistribution[μ,σ]/.questionScoreDistributionParameters,x]},
Show[
{
Plot[pdf,{x,0,50},
PlotRange -> All,PlotTheme->"Detailed",
PlotLegends->Placed[{pdf},{Right,0.75}],
PlotStyle->Red,ImageSize->400
],
ListPlot[
{#1,#2/Length[questionScoresBelowFifty]}&@@@Tally[questionScoresBelowFifty],
PlotRange->All,
Filling->Axis,
PlotStyle->Blue
]
}
]
]
|
Words Much More Common in Mathematics Than Normal Language
There are many words that appear in mathematics that are not found in typical English. Some examples include names of mathematicians (e.g. Riemann, Euler, etc.) or words that have special meanings (integral, matrix, group, ring, etc.).
We can start to investigate these words by gathering all of the post bodies:
|
✕
postBodies=EntityValue["StackExchange.Mathoverflow:Post","Body"]; |
We’ll need to create functions to normalize strings (normalizeString) and extract sentences (extractSentences), removing HTML tags and replacing any equations with “![]() ”:
”:

✕
normalizeString=StringReplace[
{
Shortest["$$"~~__~~"$$"]:>"\[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH]",
Shortest["$"~~__~~"$"]->"\[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH]",
Shortest["\\begin{equation*}"~~__~~"\\end{equation*}"]->"\[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH]",
Shortest["\\begin{align}"~~__~~"\\end{align}"]->"\[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH]",
Shortest[""]->"",
Shortest["
|
We’ll also need to extract, count up and sort the words from all of the post bodies:

✕
wordToCount=postBodies//RightComposition[ extractSentences, Flatten/*StringSplit/*ToLowerCase, Flatten, Counts/*ReverseSort ]; |
This gives a list of almost 400k words:

✕
wordToCount//Length |
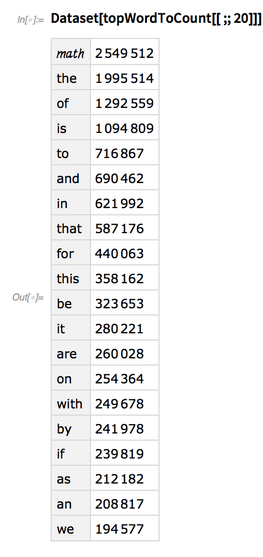
We can trim it down to just the top 500 words, being careful to remove some extra noise with websites, equations, inequalities and single letters:

✕
topWordToCount=KeySelect[ wordToCount[[;;1000]], Not[StringMatchQ[#, "*'*"|"*=*"|"*<*"|"*www*"|"http"|"https"|"--"]]&&StringLength[#]>1& ]//Take[#,UpTo[500]]&; |
Note that “![]() ” is the most common word, since all equations were replaced with it:
” is the most common word, since all equations were replaced with it:
✕
Dataset[topWordToCount[[;;20]]] |
It’s useful to visualize it as a word cloud:

✕
WordCloud[topWordToCount] |
Removing “![]() ” and stopwords like “the”, “is” and “of” from the data will avoid some clutter:
” and stopwords like “the”, “is” and “of” from the data will avoid some clutter:

✕
topWordToCountNoStopwords=KeySelect[ wordToCount[[;;1000]], Not[StringMatchQ[#, "*'*"|"*=*"|"*<*"|"*www*"|"http"|"https"|"\[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH]"|"--"]]&&StringLength[#]>1& ]; topWordToCountNoStopwords=KeyTake[topWordToCountNoStopwords,topWordToCountNoStopwords//Keys//DeleteStopwords]//Take[#,UpTo[500]]&; |

✕
Dataset[topWordToCountNoStopwords[[;;20]]] |
Now the results are more interesting and meaningful:

✕
WordCloud[topWordToCountNoStopwords] |
Of course, we can take this analysis further. We can get the frequencies for the top words in usual English with WordFrequencyData:

✕
wordToEnglishFrequency=WordFrequencyData[Keys[topWordToCountNoStopwords]];//AbsoluteTiming |
Normalize the counts of the words on MathOverflow, and then join the two as coordinates in 2D frequency space:

✕
wordToMOFrequency=N[topWordToCountNoStopwords/Total[topWordToCountNoStopwords]]; |

✕
wordToFrequencyCoordinates={wordToEnglishFrequency,wordToMOFrequency}//Merge[Identity]//Select[FreeQ[_Missing]];
|

✕
wordToFrequencyCoordinates[[;;3]] |
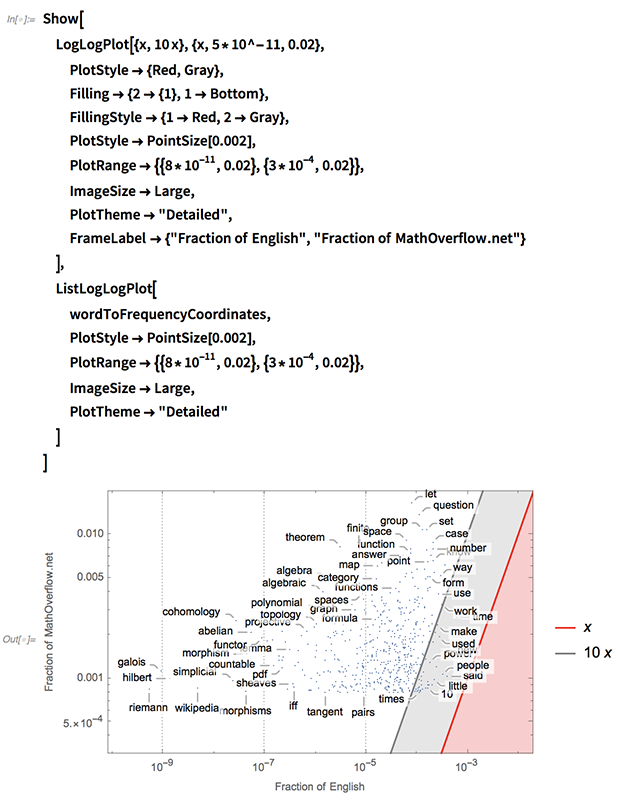
We can visualize these coordinates, adding a red region to the plot for words more commonly used in typical English than in MathOverflow posts (below  =
=  ), and a gray region for words that are more commonly used in MathOverflow posts by less than a factor of 10 (below
), and a gray region for words that are more commonly used in MathOverflow posts by less than a factor of 10 (below  = 10
= 10  ).
).
This arbitrary factor allows us to narrow down the words that are much more common to MathOverflow than typical English, which appear in the white region (above  = 10
= 10  ):
):
✕
Show[
LogLogPlot[{x,10x},{x,5*10^-11,0.02},
PlotStyle->{Red,Gray},
Filling->{2->{1},1->Bottom},
FillingStyle->{1->Red,2->Gray},
PlotStyle->PointSize[0.002],
PlotRange->{{8*10^-11,0.02},{3*10^-4,0.02}},
ImageSize->Large,
PlotTheme->"Detailed",
FrameLabel->{"Fraction of English","Fraction of MathOverflow.net"}
],
ListLogLogPlot[
wordToFrequencyCoordinates,
PlotStyle->PointSize[0.002],
PlotRange->{{8*10^-11,0.02},{3*10^-4,0.02}},
ImageSize->Large,
PlotTheme->"Detailed"
]
]
|
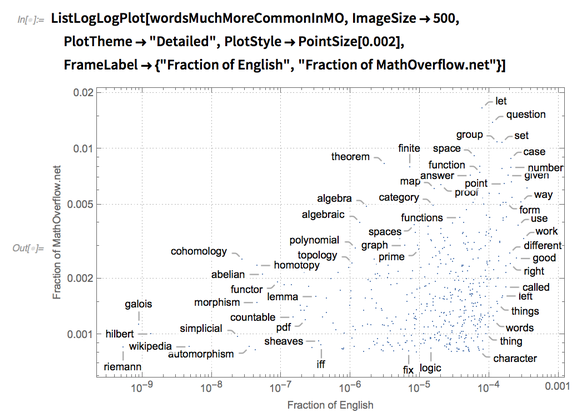
We can take this another step further by looking at the words in the white region that are much more likely to occur on MathOverflow than they are in typical English:

✕
wordsMuchMoreCommonInMO=wordToFrequencyCoordinates//Select[Apply[Divide]/*LessThan[1/10]]; wordsMuchMoreCommonInMO//Length |
✕
ListLogLogPlot[wordsMuchMoreCommonInMO,ImageSize->500,PlotTheme->"Detailed",PlotStyle->PointSize[0.002],FrameLabel->{"Fraction of English","Fraction of MathOverflow.net"}]
|
Of course, an easy way to visualize this data is in a word cloud, where the words are weighted by combining their frequency of use via Norm:

✕
WordCloud[Norm/@wordsMuchMoreCommonInMO,WordSpacings->2] |
Analysis of n-Grams
Of course, individual words are not the only way to analyze the MathOverflow corpus.
We can create a function to compute  -grams using Partition and recycling extractSentences from earlier:
-grams using Partition and recycling extractSentences from earlier:

✕
ClearAll[getNGrams]; getNGrams[n_Integer?Positive]:=RightComposition[ extractSentences, Map[ ToLowerCase/*StringSplit/*Map[Counts[Partition[#,n,1]]&]/*Merge[Total] ], Merge[Total], ReverseSort, (* Keep only the top 10,000 to save memory *) Take[#,UpTo[10000]]& ]; |
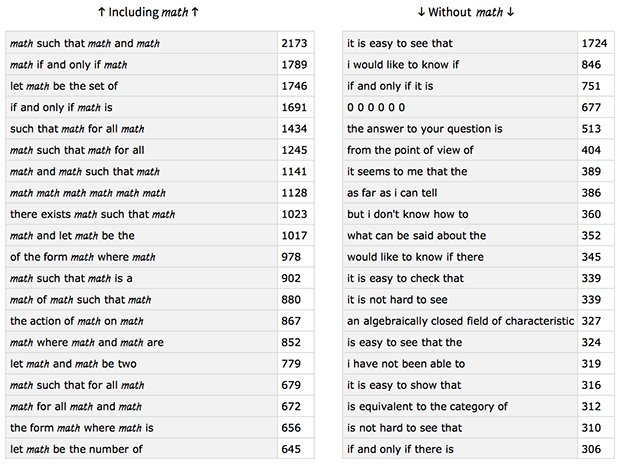
Next, we’ll need to build a function to show the  -grams in tables and word clouds, both with and without math (since putting them together would clutter the results a bit):
-grams in tables and word clouds, both with and without math (since putting them together would clutter the results a bit):
![ClearAll[showNGrams]; ClearAll[showNGrams];](https://content.wolfram.com/sites/39/2019/01/img117.png)
✕
ClearAll[showNGrams];
showNGrams[nGramToCount_Association]:=Module[
{phraseToCount,phraseToCountWithMath,phraseToCountWithoutMath},
phraseToCount=KeyMap[StringRiffle,nGramToCount];
phraseToCountWithMath=Take[phraseToCount,UpTo[200]]//Normal//Select[#,Not@StringFreeQ[#[[1]],"\[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH]"]&,50]&//Association;
phraseToCountWithoutMath=Take[phraseToCount,UpTo[200]]//Normal//Select[#,StringFreeQ[#[[1]],"\[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH]"]&,50]&//Association;
Print@WordCloud[Take[phraseToCountWithMath,UpTo[50]],ImageSize->500,WordSpacings->2];
Print[
Row[
{
Column[{Style["↑ Including \[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH] ↑",24,FontFamily->"Source Code Pro"],Dataset[Take[phraseToCountWithMath,UpTo[20]]]}],
Column[{Style["↓ Without \[ScriptCapitalM]\[ScriptCapitalA]\[ScriptCapitalT]\[ScriptCapitalH] ↓",24],Dataset[Take[phraseToCountWithoutMath,UpTo[20]]]}]
},
Spacer[20]
]
];
Print@WordCloud[Take[phraseToCountWithoutMath,UpTo[50]],ImageSize->500,WordSpacings->2];
];
|
3-grams
Looking at the 3-grams, there are lots of “The number of…”, “The set of…”, “is there a…” and more.
There are definitely signs of “if and only if,” but they’re not well captured here since we’re looking at 3-grams. They should show up later in the 4-grams, anyway.
There is a lot of of “Let ![]() be…”, “
be…”, “![]() is a,” and similar—it’s clear that MathOverflow users frequently use
is a,” and similar—it’s clear that MathOverflow users frequently use  for mathematical notation:
for mathematical notation:
|
✕
postBodies//getNGrams[3]//showNGrams |
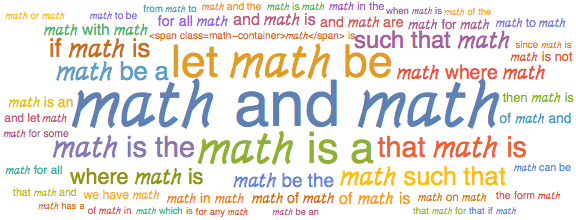


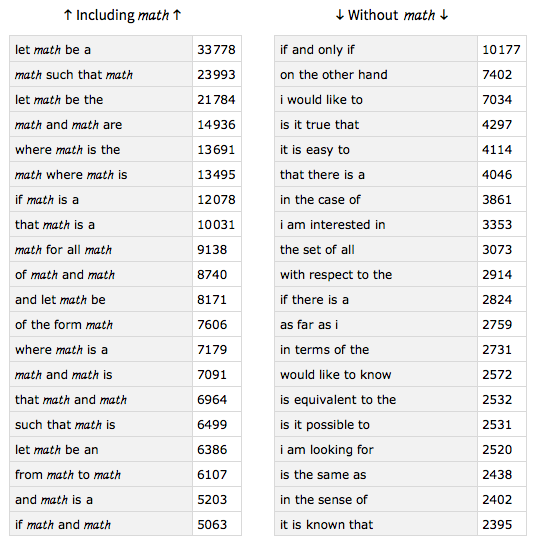
4-grams
Expanding on the 3-grams, the 4-grams give several mathy phrases like “if and only if,” “on the other hand,” “is it true that” and “the set of all.”
We also see more proof-like phrases like “Let ![]() be a,” “
be a,” “![]() such that
such that ![]() ” and similar.
” and similar.
It’s interesting how the two word clouds begin to show the split of “proof-like” phrases and “natural language” phrases:
|
✕
postBodies//getNGrams[4]//showNGrams |
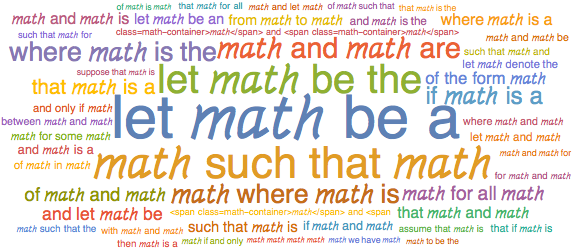

5-grams
We see similar trends with the 5- and 6-grams:
|
✕
postBodies//getNGrams[5]//showNGrams |
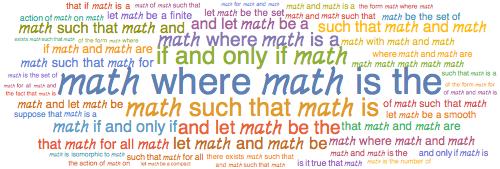


6-grams
|
✕
postBodies//getNGrams[6]//showNGrams |
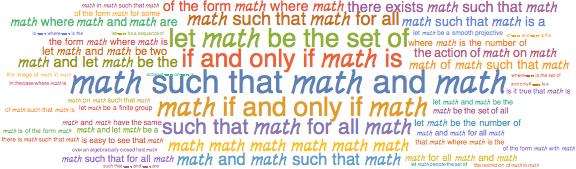

“Post Thread” Networks
Moving past natural language processing, another way to analyze the MathOverflow site is as a network.
We can create a network of MathOverflow users that communicate with each other. One way to do this is to connect two users if one user posts an answer to another user’s question. In this way, we can create a directed graph of MathOverflow users.
Although it’s possible to do this graph-like traversal and matching with the usual EntityValue syntax, it could get somewhat messy.
Questioner-Answerer Network
To start, we can write a symbolic representation of a SPARQL query to find all connections between question writers and the writers of answers, and then do some processing to turn it into a Graph:
|
✕
Needs["GraphStore`"] |

✕
questionerToAnswererGraph=Entity["StackExchange.Mathoverflow:Post"]//RightComposition[
SPARQLSelect[
{
RDFTriple[SPARQLVariable["post"],post type,Entity["StackExchange:PostType", "1"]],
SPARQLPropertyPath[SPARQLVariable["post"],{owner},SPARQLVariable["questioner"]],
SPARQLPropertyPath[SPARQLVariable["post"],{SPARQLInverseProperty[parent post],owner},SPARQLVariable["answerer"]]
}->{SPARQLVariable["questioner"],SPARQLVariable["answerer"]}
],
Lookup[#,{SPARQLVariable["answerer"],SPARQLVariable["questioner"]}]&,
Map[Apply[DirectedEdge]],
Graph
]
|

From the icon of the output, we can see it’s a very large directed multigraph. Networks of this size have very little hope of being visualized easily, so we should find a way to reduce the size of it.
Smaller Questioner-Answerer Network
We can trim down the size by writing a similar SPARQL query that limits us to posts with a few numerical mathematics post tags:

✕
questionerToAnswererGraphSmaller=Entity["StackExchange.Mathoverflow:Post"]//RightComposition[
SPARQLSelect[
{
RDFTriple[SPARQLVariable["post"],post type,Entity["StackExchange:PostType", "1"]],
Alternatives[
RDFTriple[SPARQLVariable["post"],tags,Entity["StackExchange.Mathoverflow:Tag", "NumericalLinearAlgebra"]],
RDFTriple[SPARQLVariable["post"],tags,Entity["StackExchange.Mathoverflow:Tag", "NumericalAnalysisOfPde"]],
RDFTriple[SPARQLVariable["post"],tags,Entity["StackExchange.Mathoverflow:Tag", "NumericalIntegration"]],
RDFTriple[SPARQLVariable["post"],tags,Entity["StackExchange.Mathoverflow:Tag", "RecreationalMathematics"]]
],
SPARQLPropertyPath[SPARQLVariable["post"],{owner},SPARQLVariable["questioner"]],
SPARQLPropertyPath[SPARQLVariable["post"],{SPARQLInverseProperty[parent post],owner},SPARQLVariable["answerer"]]
}->{SPARQLVariable["questioner"],SPARQLVariable["answerer"]}
],
Lookup[#,{SPARQLVariable["answerer"],SPARQLVariable["questioner"]}]&,
Map[Apply[DirectedEdge]],
Graph[#,GraphStyle->"LargeGraph"]&
]
|
This graph is much smaller and can be more reasonably visualized. For simplicity, let’s focus only on the largest (weakly) connected component:

✕
questionerToAnswererGraphSmallerConnected=First@WeaklyConnectedGraphComponents[questionerToAnswererGraphSmaller] |
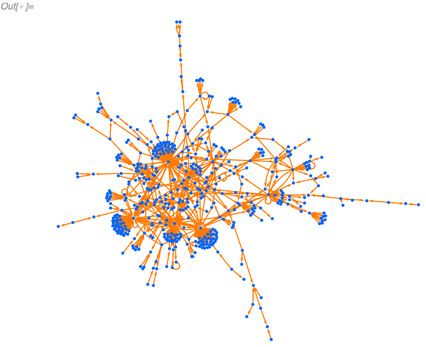
Questioner-Answerer Communities by Geographic Region
We can group the vertices of the graph (MathOverflow users) by geography by using the location information users have entered into their profiles.
Here, we can use Interpreter["Location"] to handle a variety of input forms, including countries, cities, administrative divisions (such as states) and universities:

✕
userToLocation=EntityValue[VertexList[questionerToAnswererGraphSmallerConnected],"Location","NonMissingEntityAssociation"]; userToLocation=AssociationThread[Keys[userToLocation],Interpreter["Location"]@RemoveDiacritics@Values[userToLocation]]; |
The results are pretty good, giving over 250 approximate locations:
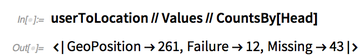
✕
userToLocation//Values//CountsBy[Head] |
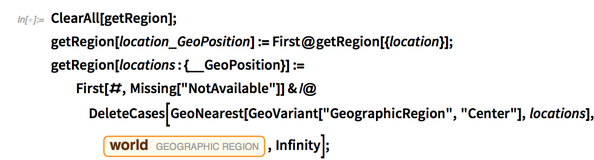
Of course, these individual locations are not that helpful, as they are very localized. We can use GeoNearest to find the nearest geographic region as a basis for determining groups for the users:
✕
ClearAll[getRegion];
getRegion[location_GeoPosition]:=First@getRegion[{location}];
getRegion[locations:{__GeoPosition}]:=First[#,Missing["NotAvailable"]]&/@DeleteCases[GeoNearest[GeoVariant["GeographicRegion","Center"],locations],Entity["GeographicRegion", "World"],Infinity];
|
Next, we group users into communities based on this geographic information:

✕
userToGeographicRegion=DeleteMissing@AssociationThread[Keys[#],getRegion@Values[#]]&[Select[userToLocation,MatchQ[_GeoPosition]]]; geographicRegionToUsers=GroupBy[userToGeographicRegion,Identity,Keys]; |

✕
Length/@geographicRegionToUsers |
Lastly, we can use CommunityGraphPlot to build a graphic that shows the geographic communities of the questioner-answerer network:

✕
regionToPointColor=Lookup[
<|
Entity["GeographicRegion", "Europe"]->Darker@,Entity["GeographicRegion", "NorthAmerica"]->Darker[Green,0.5],Entity["GeographicRegion", "Australia"]->Orange,Entity["GeographicRegion", "Asia"]->Purple,Entity["GeographicRegion", "SouthAmerica"]->Darker[Red,0.25]
|>,
#,Brown]&;
regionToLabelPlacement=Lookup[
<|
Entity["GeographicRegion", "Europe"]->Below,Entity["GeographicRegion", "NorthAmerica"]->After,Entity["GeographicRegion", "Asia"]->Below
|>,
#,Above]&;
regionToRotation=Lookup[<|Entity["GeographicRegion", "NorthAmerica"]->-(π/2)|>,#,0]&;
allRegionsToUsers=Append[geographicRegionToUsers,"???"->Complement[VertexList[questionerToAnswererGraphSmallerConnected],Flatten@Values[geographicRegionToUsers]]];
styledCommunities=KeyValueMap[
Function[
{region,users},
With[
{regionPointColor=regionToPointColor[region]},
Labeled[
Style[users,regionPointColor],
Rotate[
Style[
Framed[region,Background->regionPointColor,RoundingRadius->5,FrameMargins->Small],
FontColor->ResourceFunction["FontColorFromBackgroundColor"][regionPointColor],
FontSize->12
],
regionToRotation[region]
],
regionToLabelPlacement[region]
]
]
],
allRegionsToUsers
];
CommunityGraphPlot[questionerToAnswererGraphSmallerConnected,styledCommunities,
ImageSize->500,
Method->"Hierarchical",
EdgeStyle->Directive[Opacity[0.25,Black],Arrowheads[Tiny]],
VertexStyle->PointSize[Medium],
CommunityRegionStyle->(Opacity[0.1,regionToPointColor[#]]&/@Keys[allRegionsToUsers]),
CommunityBoundaryStyle->(Opacity[1,Black]&/@Keys[allRegionsToUsers])
]
|
Post Owner-Commenter Network
Of course, we could do a similar analysis on connections between post owners and their commenters for posts tagged with “linear-programming”:
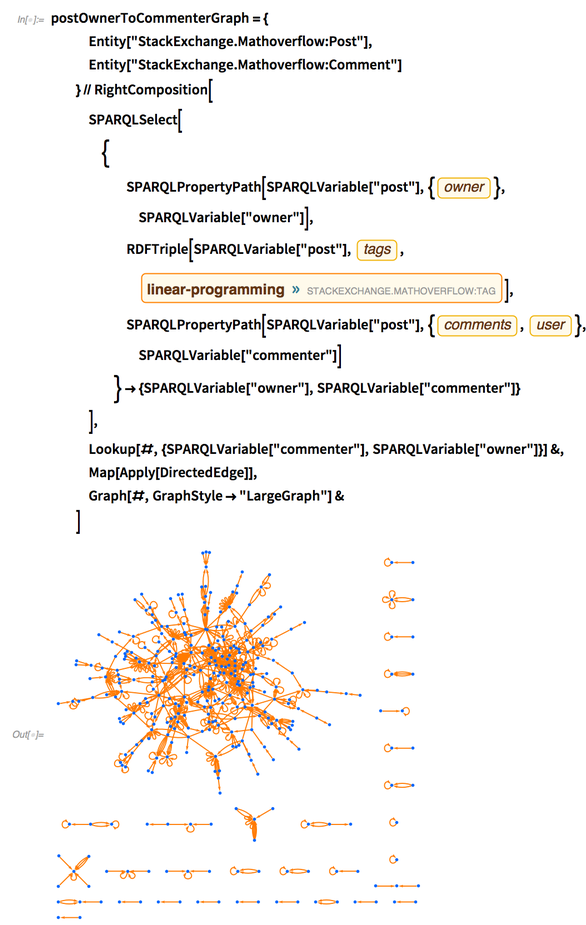
✕
postOwnerToCommenterGraph={
Entity["StackExchange.Mathoverflow:Post"],Entity["StackExchange.Mathoverflow:Comment"]
}//RightComposition[
SPARQLSelect[
{
SPARQLPropertyPath[SPARQLVariable["post"],{owner},SPARQLVariable["owner"]],
RDFTriple[SPARQLVariable["post"],tags,Entity["StackExchange.Mathoverflow:Tag", "LinearProgramming"]],
SPARQLPropertyPath[SPARQLVariable["post"],{comments,user},SPARQLVariable["commenter"]]
}->{SPARQLVariable["owner"],SPARQLVariable["commenter"]}
],
Lookup[#,{SPARQLVariable["commenter"],SPARQLVariable["owner"]}]&,
Map[Apply[DirectedEdge]],
Graph[#,GraphStyle->"LargeGraph"]&
]
|
However, further analysis on this network will be left as an exercise for the reader.
Analyzing TEX Snippets
![]() , in its various forms, has been around for over 40 years, and is widely used in math and science for typesetting.
, in its various forms, has been around for over 40 years, and is widely used in math and science for typesetting.
On MathOverflow, there are not many posts without it, so exploring ![]() snippets can give interesting insights into the content available on the site.
snippets can give interesting insights into the content available on the site.
Extract TEX Snippets
First, we need to extract the ![]() snippets from post bodies. Consider a simple example post:
snippets from post bodies. Consider a simple example post:

✕
Entity["StackExchange.Mathoverflow:Post", "40686"]["Body"] |
We can write a function to extract the 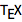 snippets in a string, noting the two main input forms ("
snippets in a string, noting the two main input forms ("

✕
ClearAll[extractTeXSnippets];
extractTeXSnippets[s_String] :=
Module[
{dd,d,o},
dd=StringCases[s,Shortest["$$"~~__~~"$$"]];
d=StringCases[StringReplace[s,Shortest["$$"~~__~~"$$"]:>""],Shortest["$"~~__~~"$"]];
o=StringCases[
s,
Alternatives[
Shortest["\\begin{equation*}"~~__~~"\\end{equation*}"],
Shortest["\\begin{align}"~~__~~"\\end{align}"]
]
];
StringReplace[Join[dd, d,o], {".$":>"$"}]
]
|
Testing this on the simple example gives the snippets wrapped in dollar signs:

✕
extractTeXSnippets[body] |
Format TEX Snippets
Of course, once we have ![]() snippets, it would be valuable to format them into actual typesetting that’s easier on the eyes than the raw
snippets, it would be valuable to format them into actual typesetting that’s easier on the eyes than the raw ![]() code.
code.
We can write a quick function to do this with proper formatting:

✕
blackboardBoldRules=character to double struck;
frakturGothicRules=character to gothic;
formatTeXSnippet[s_String] :=
Which[
StringMatchQ[s, "$\\mathbb{"~~ _ ~~ "}$"],
StringReplace[s,"$\\mathbb{"~~ a_ ~~ "}$":> a]/.blackboardBoldRules,
StringMatchQ[s, "$\\mathbb "~~ _ ~~ "$"],
StringReplace[s,"$\\mathbb "~~ a_ ~~ "$":> a]/.blackboardBoldRules,
StringMatchQ[s, "$\\mathfrak{"~~ _ ~~ "}$"],
StringReplace[s,"$\\mathfrak{"~~ a_ ~~ "}$":> a]/.frakturGothicRules,
StringMatchQ[s, "$\\mathfrak "~~ _ ~~ "$"],
StringReplace[s,"$\\mathfrak "~~ a_ ~~ "$":> a]/.frakturGothicRules,
StringMatchQ[s, "$\\mathcal{"~~ _ ~~ "}$"],
Style[StringReplace[s,"$\\mathcal{"~~ a_ ~~ "}$":>a],FontFamily->"Snell Roundhand"],
StringMatchQ[s, "$\\mathcal "~~ _ ~~ "$"],
Style[StringReplace[s,"$\\mathcal "~~ a_ ~~ "$":>a],FontFamily->"Snell Roundhand"],
True,
StringReplace[s,"␣"->"_"]//RightComposition[
ImportString[#,"TeX"]&,
FirstCase[#,c:Cell[_,"InlineFormula"|"NumberedEquation"]:>DisplayForm[c],Missing["NotAvailable"],∞]&
]
]
|
We can test the results on the previously extracted ![]() snippets:
snippets:

✕
AssociationMap[formatTeXSnippet,extractTeXSnippets[body]]//KeyValueMap[List]//Grid[#,Frame->All]& |
We can also test them on a completely different post:
![["Body"] // ["Body"] //](https://content.wolfram.com/sites/39/2019/01/img119.png)
✕
Entity["StackExchange.Mathoverflow:Post", "40686"]["Body"] //
extractTeXSnippets // AssociationMap[formatTeXSnippet] //
KeyValueMap[List] // Grid[#, Frame -> All, Alignment -> Left] &
|
Set Up TEX Snippets Property
This system works well, so we should make it easier to use. We can do this by hooking up these functions as a property for posts, keeping the formatting function separate so that analysis can still be done on the raw strings:

✕
EntityProperty["StackExchange.Mathoverflow:Post","TeXSnippets"]["Label"]="TEX snippets"; EntityProperty["StackExchange.Mathoverflow:Post","TeXSnippets"]["DefaultFunction"]=Function[entity, extractTeXSnippets[entity["Body"]] ]; |
Now we can just call the property on an entity instead:
!["TeXSnippets"] // Map[formatTeXSnippet] "TeXSnippets"] // Map[formatTeXSnippet]](https://content.wolfram.com/sites/39/2019/01/img120.png)
✕
Entity["StackExchange.Mathoverflow:Post", "67739"]["TeXSnippets"]//Map[formatTeXSnippet] |
From here, it should be easy to extract all of the ![]() fragments from all of the posts:
fragments from all of the posts:
|
✕
allTeXSnippets=EntityValue["StackExchange.Mathoverflow:Post","TeXSnippets"]; |
Create a TEX Word Cloud
A simple way to analyze the ![]() snippets is to count up the number of times each fragment is used:
snippets is to count up the number of times each fragment is used:
|
✕
teXToCount=allTeXSnippets//RightComposition[Flatten,Counts,ReverseSort]; |
There are almost one million unique ![]() snippets used in the post bodies on MathOverflow:
snippets used in the post bodies on MathOverflow:

✕
teXToCount//Length |
We can also make a simple word cloud from the top 100 snippets:
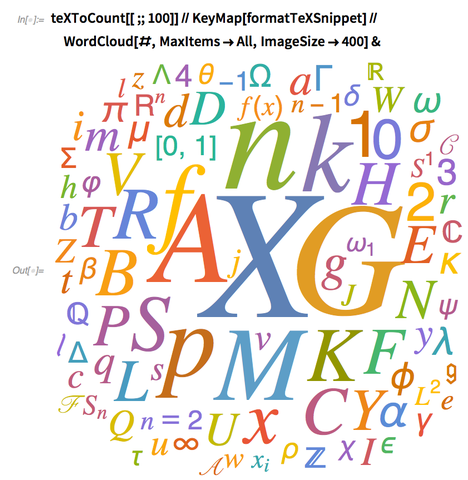
✕
teXToCount[[;;100]]//KeyMap[formatTeXSnippet]//WordCloud[#,MaxItems->All,ImageSize->400]& |
It’s easy to see that there are a lot of single-letter snippets. But there are a lot more interesting things hiding beyond these top 100. Let’s take a look at a few different cases!
Integrals
Integrals are fairly easy to find with some simple string pattern matching:

✕
integralToCount=KeySelect[teXToCount,StringMatchQ[("$"|"$$")~~(Whitespace|"")~~"\\int"~~__~~"$"]];
integralToCount//Length
|
Looking at the top 50 gives some interesting results—some very simple, and some rather complex:

✕
WordCloud[integralToCount[[;;50]]//KeyMap[formatTeXSnippet],ImageSize->400,WordSpacings->2] |
Analyze Equations
Another interesting subset of ![]() snippets to consider is equations. Again, we can find these with some string pattern matching that requires an equals sign:
snippets to consider is equations. Again, we can find these with some string pattern matching that requires an equals sign:

✕
equations=KeySelect[teXToCount,StringMatchQ[("$"|"$$")~~(Whitespace|"")~~__~~" = "~~__~~"$"]];
equations//Length
|
Visualizing the top 50 gives mostly single-letter variable assignments to numbers:

✕
WordCloud[equations[[;;50]]//KeyMap[formatTeXSnippet],ImageSize->400,WordSpacings->2] |
Equations of the Form <letter> = <number>
If we look at the single-letter variable assignments, we can find the minimum and maximum values of <number> for each <letter>.
Note that this includes a list of special ![]() characters, such as \alpha:
characters, such as \alpha:
|
✕
teXRepresentationToCharacter=TeX to character; |
|
✕
specialLettersPattern=Alternatives@@Keys[teXRepresentationToCharacter]; |

✕
variableEqualsNumberDistributions=equations//Keys//StringCases[("$$"|"$")~~lhs:(specialLettersPattern|LetterCharacter)~~(Whitespace|"")~~"="~~(Whitespace|"")~~rhs:NumberString~~(Whitespace|"")~~("$$"|"$"):>Rule[ToUpperCase[lhs/.teXRepresentationToCharacter],ToExpression[rhs]]]//Merge[Counts];
|

✕
KeySort[MinMax/@Keys/@variableEqualsNumberDistributions]//KeyValueMap[Prepend[N@#2,#1<>" | "<>ToLowerCase[#1]]&]//Grid[#,Frame->All]& |
It’s interesting to see that most letters are positive, but S is strangely very negative. It’s also interesting to note the very large scale of U, V and W. Perhaps not surprisingly, N is the most common letter, though its neighbor O is the least common:
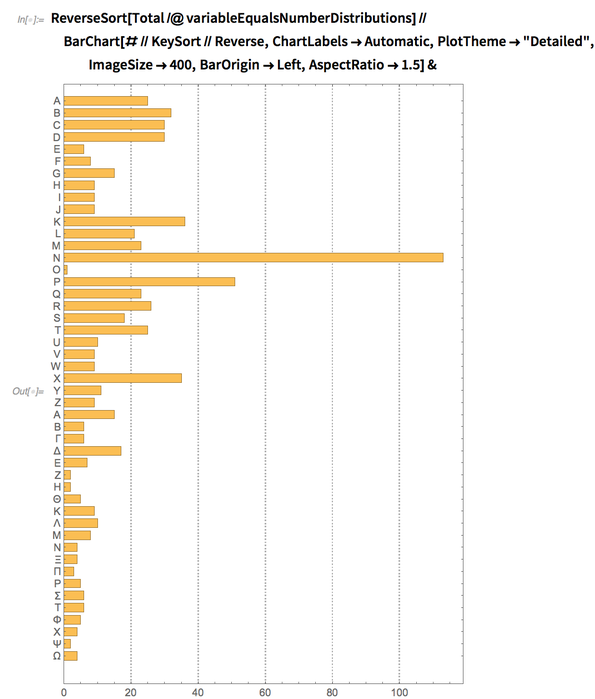
✕
ReverseSort[Total/@variableEqualsNumberDistributions]//BarChart[#//KeySort//Reverse,ChartLabels->Automatic,PlotTheme->"Detailed",ImageSize->400,BarOrigin->Left,AspectRatio->1.5]& |
Trimming these single-variable assignments out of the original equation word cloud makes the results a bit more diverse:

✕
WordCloud[
KeySelect[equations,StringMatchQ[("$$"|"$")~~(specialLettersPattern|LetterCharacter)~~(Whitespace|"")~~"="~~(Whitespace|"")~~NumberString~~(Whitespace|"")~~("$$"|"$")]/*Not][[;;50]]//KeyMap[formatTeXSnippet],
ImageSize->400,
WordSpacings->2
]
|
Equations of the Form <letter> = <letter>
It’s interesting to see that there are a lot of letters assigned to (or compared with) another letter. We can make a simple graph that connects two letters in these equations, again taking into account special characters like \alpha:

✕
letterGraph=Keys[equations]//StringCases[("$$"|"$")~~lhs:(specialLettersPattern|LetterCharacter)~~(Whitespace|"")~~"="~~(Whitespace|"")~~rhs:LetterCharacter~~(Whitespace|"")~~("$$"|"$"):>(DirectedEdge[lhs,rhs]/.teXRepresentationToCharacter)]//Flatten//Counts//KeySortBy[First];
|
The graph, without combining upper and lowercase letters, is quite messy:

✕
Graph[ Union@Cases[Keys[letterGraph],_String,Infinity], Keys[letterGraph], GraphLayout->"CircularEmbedding", EdgeWeight->Normal[letterGraph], EdgeStyle->Normal[Opacity[N@(#/Max[letterGraph])]&/@letterGraph], VertexLabels->Placed[Automatic,Center], VertexLabelStyle->Directive[Bold,Small], VertexSize->Large, PlotTheme->"Web", ImageSize->400 ] |
If we combine the upper and lowercase letters, the graph becomes a little bit cleaner:

✕
upperCaseLetterGraph=Merge[Normal[letterGraph]/.c_String:>ToUpperCase[c],Total]; Graph[ Union@Cases[Keys[upperCaseLetterGraph],_String,Infinity], Keys[upperCaseLetterGraph], GraphLayout->"CircularEmbedding", EdgeWeight->Normal[upperCaseLetterGraph], EdgeStyle->Normal[Opacity[N@(#/Max[letterGraph])]&/@upperCaseLetterGraph], VertexLabels->Placed[Automatic,Center], VertexLabelStyle->Bold, VertexSize->Large, PlotTheme->"Web", ImageSize->400 ] |
If we again remove these equation types, the word cloud becomes even cleaner:

✕
WordCloud[
KeySelect[equations,StringMatchQ[
Alternatives[
("$$"|"$")~~(specialLettersPattern|LetterCharacter)~~(Whitespace|"")~~"="~~(Whitespace|"")~~NumberString~~(Whitespace|"")~~("$$"|"$"),
("$$"|"$")~~(specialLettersPattern|LetterCharacter)~~(Whitespace|"")~~"="~~(Whitespace|"")~~LetterCharacter~~(Whitespace|"")~~("$$"|"$")
]
]/*Not][[;;50]]//KeyMap[formatTeXSnippet],
ImageSize->400,
WordSpacings->2
]
|
Functional Equations
Another interesting subset of equations to look into is functional equations. With a little bit of string pattern matching, we can find many examples:
✕
functionalEquations=KeySelect[equations,StringMatchQ[___~~(f:_)~~"("~~__~~")"~~__~~(f:_)~~"("~~__~~")"~~___]];
functionalEquations//Length
|

✕
functionalEquations[[;;16]]//Keys//Map[formatTeXSnippet]//Multicolumn[#,Frame->All]& |
By focusing on functional equations that have one function with arguments on the left side of an equals sign, we get fewer results:

✕
functionalEquations2=KeySelect[equations,StringMatchQ[("$$"|"$")~~(f:LetterCharacter)~~"("~~__~~")"~~(Whitespace|"")~~"="~~(Whitespace|"")~~__~~(f:_)~~"("~~__~~")"~~___~~("$$"|"$")]];
functionalEquations2//Length
|

✕
functionalEquations2[[;;16]]//Keys//Map[formatTeXSnippet]//Multicolumn[#,Frame->All]& |
However, we’ll need to go further to find equations that are easier to work with. Let’s limit ourselves to single-letter, single-argument functions:

✕
functionalEquations3=KeySelect[equations,StringMatchQ[("$$"|"$")~~(f:LetterCharacter)~~"("~~x:LetterCharacter~~")"~~(Whitespace|"")~~"="~~(Whitespace|"")~~__~~(f:_)~~"("~~x:_~~")"~~___~~("$$"|"$")]];
functionalEquations3//Length
|

✕
functionalEquations3[[;;16]]//Keys//Map[formatTeXSnippet]//Multicolumn[#,Frame->All]& |
This is much more pointed, but we can go further. If we limit ourselves to functional equations with only one equals sign with single, lowercased arguments that only consist of a single head and argument (modulo operators and parentheses), we find just six equations:

✕
functionalEquations4=KeySelect[
equations,
StringMatchQ[s:(("$$"|"$")~~(f:LetterCharacter)~~"("~~x:LetterCharacter?LowerCaseQ~~")"~~(Whitespace|"")~~"="~~(Whitespace|"")~~__~~(f:_)~~"("~~x:_~~")"~~___~~("$$"|"$"))/;(StringCount[s,"="]===1&&StringFreeQ[s,"\\"~~LetterCharacter..]&&Complement[Union[Characters[s]],{"$","^","(",")","-","+","=","{","}","."," ","0","1","2","3","4","5","6","7","8","9"}]===Sort[{f,x}])]
];
functionalEquations4//Length
|

✕
functionalEquations4//Keys//Map[formatTeXSnippet]//Column[#,Frame->All]& |
Interestingly, there are only two functionally unique equations in this list:
f(x) = 1 + x f(x)^2
f(x) = 1 + x^2 f(x)^2
If we clean up these functional equations, we can put them through Interpreter["TeXExpression"] to get actual Wolfram Language representations of them:

✕
interpretedFunctionalEquations=Interpreter["TeXExpression"][StringReplace[f:LetterCharacter~~"("~~x:LetterCharacter~~")^"~~("{"|"")~~n:DigitCharacter~~("}"|""):>"("<>f<>"("<>x<>")"<>")^"<>n]/@Keys[functionalEquations4]]/.C[x_]:>F[x]
|
Finally, we can solve these equations with RSolve:

✕
AssociationMap[ Replace[eqn:((f_)[x_]==rhs_):>RSolve[eqn,f[x],x]], interpretedFunctionalEquations ] |
Analyze “Big O” Notation Arguments
Moving past equations, another common notation among mathematicians is big O notation. Frequently used in computational complexity and numerical error scaling, this notation should surely appear somewhat frequently on MathOverflow.
Let’s take a look by finding ![]() snippets wrapped in O that consist of a single argument and have equal numbers of open-and-close parentheses:
snippets wrapped in O that consist of a single argument and have equal numbers of open-and-close parentheses:

✕
bigONotationArguments=StringCases[Keys[teXToCount],Shortest["O("~~args__~~")"]/;StringFreeQ[args,","|";"]&&StringCount[args,"("]===StringCount[args,")"]:>"$$"<>args<>"$$"]//Flatten//Counts//ReverseSort;
bigONotationArguments//Length
|
The results are varied:

✕
bigONotationArguments[[;;100]]//KeyMap[formatTeXSnippet]//WordCloud[#,WordSpacings->3]& |
One can note that many of these results are functionally equivalent—they differ only in the letter chosen for the variable.
We can clean these cases up with a little bit of effort:

✕
normalizeBigOStrings=StringReplace[
{
(* Any constant number 1 *)
"$$"~~NumberString~~"$$"->"$$1$$",
"$$"~~LetterCharacter~~"$$"->"$$n$$",
"$$"~~LetterCharacter~~"^"~~exp:(DigitCharacter|("{"~~__~~"}"))~~"$$":>"$$n^"<>exp<>"$$",
"$$"~~LetterCharacter~~"\\log "~~LetterCharacter~~"$$":>"$$n\\log n$$",
"$$"~~b:DigitCharacter~~"^"~~x_~~"/"~~x_~~"$$":>"$$"<>b<>"^n/n$$",
"$$"~~numerator:DigitCharacter~~"/"~~LetterCharacter~~"$$":>"$$"<>numerator<>"/n$$",
"$$"~~factor:DigitCharacter~~LetterCharacter~~"$$":>"$$"<>factor<>"n$$",
"$$1/"~~LetterCharacter~~"^"~~exp:(DigitCharacter|("{"~~__~~"}"))~~"$$":>"$$1/n^"<>exp<>"$$",
"$$1/|"~~LetterCharacter~~"|^"~~exp:(DigitCharacter|("{"~~__~~"}"))~~"$$":>"$$1/|n|^"<>exp<>"$$",
"$$"~~LetterCharacter~~"^"~~exp:(DigitCharacter|("{"~~__~~"}"))~~"\\log "~~LetterCharacter~~"$$":>"$$n^"<>exp<>"\\log n$$",
"$$|"~~LetterCharacter~~"|^"~~exp:(DigitCharacter|("{"~~__~~"}"))~~"$$":>"$$|n|^"<>exp<>"$$",
"$$\\"~~op:("log"|"dot")~~Whitespace ~~LetterCharacter~~"$$":>"$$\\"<>op<>" n$$",
"$$\\log|"~~LetterCharacter~~"|$$"->"$$\\log|n|$$",
"$$\\sqrt{"~~LetterCharacter~~"}$$":>"$$\\sqrt{n}$$",
"$$"~~LetterCharacter~~"/\\log "~~LetterCharacter~~"$$":>"$$n/\\log n$$"
}/.LetterCharacter->(specialLettersPattern|LetterCharacter)
];
|

✕
normalizedBigOArguments=Normal[bigONotationArguments]//RightComposition[ GroupBy[#,First/*normalizeBigOStrings->Last,Total]&, ReverseSort ]; |
Now the data is much cleaner:
![normalizedBigOArguments[[;; 15]] normalizedBigOArguments[[;; 15]]](https://content.wolfram.com/sites/39/2019/01/7Janimg145.png)
✕
normalizedBigOArguments[[;;15]]//KeyMap[formatTeXSnippet]//Dataset |
![normalizedBigOArguments[[;; 100]] normalizedBigOArguments[[;; 100]]](https://content.wolfram.com/sites/39/2019/01/7Janimg146.png)
✕
normalizedBigOArguments[[;;100]]//Keys//Map[formatTeXSnippet]//Multicolumn |
And the word cloud looks much nicer:
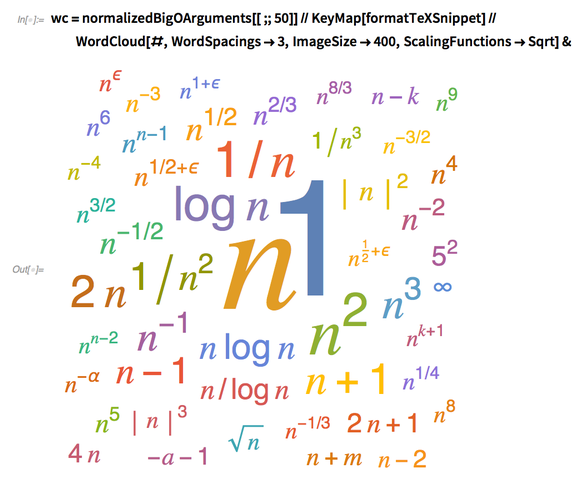
✕
wc=normalizedBigOArguments[[;;50]]//KeyMap[formatTeXSnippet]//WordCloud[#,WordSpacings->3,ImageSize->400,ScalingFunctions->Sqrt]& |
Lastly, since these are arguments to O, let’s set the word cloud as an argument of O to make a nice picture:
✕
Style[HoldForm[O][wc],90]//TraditionalForm |
Mentioned Propositions and Mathematicians
Another way to analyze MathOverflow is to look at the mathematical propositions and famous mathematicians that are mentioned in the post bodies.
An easy way to do this is to use more entity stores to keep track of the different types.
Mathematical Propositions: Build EntityStore
To begin, let’s set up an EntityStore for mathematical propositions and their types.
Specifically, we can set up "MathematicalPropositionType" for “base” words like “theorem,” “hypothesis” and “conjecture,” and "MathematicalProposition" for specific propositions like the “mean value theorem” and “Zorn’s lemma.”
The proposition types will serve as a means of programmatically finding the specific propositions, so we’ll need to pre-populate "MathematicalPropositionType" with entities, but we can leave it empty of entities for now—we’ll populate that type in the store by processing the post bodies, but we’ll do that next.
Note that I’ve added some properties to keep track of the propositions found in each post. Specifically, "Wordings" will hold an Association with strings for the keys and the counts of each of those strings for the values.
Additionally, we’ll set up "MentionedPostCount" to keep track of the number of times a post is mentioned:

✕
propositionStore=EntityStore[
{
"MathematicalPropositionType"-><|
"Entities"-><|
"Theorem"-><|"Label"->"theorem"|>,
"Hypothesis"-><|"Label"->"hypothesis"|>,
"Principle"-><|"Label"->"principle"|>,
"Conjecture"-><|"Label"->"conjecture"|>,
"Thesis"-><|"Label"->"thesis"|>,
"Lemma"-><|"Label"->"lemma"|>,
"Corollary"-><|"Label"->"corollary"|>,
"Axiom"-><|"Label"->"axiom"|>
|>,
"Properties"-><|
"Label"-><|"Label"->"label"|>
|>
|>,
"MathematicalProposition"-><|
"Entities"-><||>,
"Properties"-><|
"PropositionType"-><|
"Label"->"proposition type"
|>,
"Wordings"-><|
"Label"->"wordings",
"DefaultFunction"->Function[<||>],
"FormattingFunction"->ReverseSort
|>,
"Label"-><|
"Label"->"label",
"DefaultFunction"->Function[entity,entity["Wordings"]//Keys//First]
|>,
"MentionedPostCount"-><|
"Label"->"mentioned post count",
"DefaultFunction"->Function[0]
|>
|>
|>
}
];
EntityUnregister/@propositionStore[];
EntityRegister[propositionStore]
|
Populate
Now that the EntityStore is set up and registered, we can use the properties I set up in the store.
Let’s start with a list of theorems that don’t have names in them:

✕
$specialTheorems={"prime number theorem","central limit theorem","implicit function theorem","spectral theorem","incompleteness theorem","universal coefficient theorem","intermediate value theorem","mean value theorem","uniformization theorem","inverse function theorem","four color theorem","binomial theorem","index theorem","fundamental theorem of algebra","residue theorem","dominated convergence theorem","open mapping theorem","ergodic theorem","fundamental theorem of calculus","h-cobordism theorem","closed graph theorem","modularity theorem","adjoint functor theorem","geometrization theorem","primitive element theorem","fundamental theorem of arithmetic","fixed point theorem","4-color theorem","four colour theorem","isotopy extension theorem","proper base change theorem","well-ordering theorem","loop theorem","slice theorem","odd order theorem","isogeny theorem","group completion theorem","convolution theorem","reconstruction theorem","equidistribution theorem","contraction mapping theorem","principal ideal theorem","ergodic decomposition theorem","orbit-stabilizer theorem","4-colour theorem","tubular neighborhood theorem","three-squares theorem","martingale representation theorem","purity theorem","triangulation theorem","multinomial theorem","graph minor theorem","strong approximation theorem","universal coefficients theorem","localization theorem","positive mass theorem","identity theorem","cellular approximation theorem","transfer theorem","bounded convergence theorem","fundamental theorem of symmetric functions","subadditive ergodic theorem","annulus theorem","rank-nullity theorem","elliptization theorem"};
|
Next, we can build a function that will introduce new "MathematicalProposition" entities, keeping track of how often they are mentioned, their types and specific wordings for later use in cleaning things up.
Note that we strip off any possessives and remove special characters via RemoveDiacritics:

✕
ToCamelCase[s_String]:=First@ToCamelCase[{s}];
ToCamelCase[s:{__String}]:=StringSplit[RemoveDiacritics[s]]//Map[Capitalize/*StringJoin];
toStandardName=ToCamelCase[StringReplace[StringRiffle@StringTrim[StringSplit[#],"'s"],{"'"->"",Except[LetterCharacter|DigitCharacter]->" "}]]&;
With[
{propositionTypePattern=Alternatives@@EntityValue[EntityList["MathematicalPropositionType"],label]},
ClearAll[addPropositionEntity];
addPropositionEntity[proposition_String]:=With[
{
entity=Entity["MathematicalProposition",toStandardName[proposition]]
},
(* Keep track of mentions *)
entity["MentionedPostCount"]=Replace[entity["MentionedPostCount"],{i_Integer:>i+1,_->0}];
(* Keep track of specific wordings and their counts *)
entity["Wordings"]=Replace[Replace[entity["Wordings"],Except[_Association]-><||>],a_Association:>Append[a,proposition->Lookup[a,proposition,0]+1]];
(* Extract PropositionType *)
entity["PropositionType"]=StringCases[proposition,propositionTypePattern,IgnoreCase->True]//Replace[{{x_String,___}:>Entity["MathematicalPropositionType",Capitalize[ToLowerCase[x]]],_->Missing["NotAvailable"]}];
entity
]
];
|
Note that there are currently no proposition entities:
✕
EntityList["MathematicalProposition"] |
But if we run the list of special theorems through the function…
|
✕
addPropositionEntity/@$specialTheorems; |
… then there are proposition entities defined:

✕
EntityList["MathematicalProposition"]//Take[#,UpTo[5]]& |
We should reset counters for the introduced entities to keep things uniform (the list I provided was fabricated—those strings did not come from actual posts, so not resetting these values may throw off the numbers a bit):

✕
#["MentionedPostCount"]=0;&/@EntityList["MathematicalProposition"]; #["Wordings"]=Association[#["Label"]->1];&/@EntityList["MathematicalProposition"]; |
Of course, we can go further and detect other forms of propositions. Specifically, let’s look for propositions of the following forms:
- One of the special theorems we just introduced
- “<person name> theorem” (and similar)
- “theorem of <person name>” (and similar)
When we find these propositions, we can add them as entities to the proposition EntityStore (via addPropositionEntity), as well as store them with the posts so lookups are faster (as they will already be stored in memory through the EntityStore).
To start, we’ll need to do some normalization. Here’s a useful function that uses a list of words that should always be lowercased:

✕
$lowercaseWords= list of words that should be lowercased; lowerCaseSpecificWords= StringReplace[(#->ToLowerCase[#])&/@$lowercaseWords]; |
Additionally, here’s a list of ordinals and how to normalize them (including “Last”—for example, as in “Fermat’s last theorem”):

✕
$ordinalToWord=<|"1st"->"First","2nd"->"Second","3rd"->"Third","4th"->"Fourth","5th"->"Fifth","6th"->"Sixth","7th"->"Seventh","8th"->"Eighth","9th"->"Ninth","10th"->"Tenth","last"->"Last"|>;
$ordinals=Join[
Flatten[{ToLowerCase[#],#}&/@Values[$ordinalToWord]],
List@@Keys[$ordinalToWord]
]//ReverseSortBy[StringLength];
|
Now we can create a function to extract propositions from strings, normalize them with normalizeString from earlier and then create new "MathematicalProposition" entities using addPropositionEntity:

✕
With[
{
propositionTypePattern=EntityList["MathematicalPropositionType"]//label//Join[#,Capitalize/@#]&//Apply[Alternatives],
upperCaseWordPattern=(WordBoundary|Whitespace ~~(_?UpperCaseQ ~~ (LetterCharacter| "-"|"'")..)~~WordBoundary|Whitespace),
anyCaseWordPattern=(WordBoundary|Whitespace ~~((Alternatives@@$ordinals)|( (LetterCharacter| "-"|"'")..))~~WordBoundary|Whitespace),
possibleOrdinalPattern=(Alternatives@@$ordinals~~Whitespace)|""
},
extractNamedPropositions=RightComposition[
normalizeString,
DeleteDuplicates@Join[
(* Case 1: E.g. "central limit theorem" *)
StringCases[#,Alternatives@@$specialTheorems,IgnoreCase->True],
StringCases[
#,
Alternatives[
(* Case 3: "(nth) Theorem of Something (Something (Something))" *)
Shortest[(WordBoundary|Whitespace)~~possibleOrdinalPattern~~propositionTypePattern ~~ Whitespace~~"of"~~Longest@Repeated[upperCaseWordPattern,3]],
(* Case 2: "Something (something (something)) Theorem" *)
Shortest[(WordBoundary|Whitespace)~~(x:upperCaseWordPattern)~~Longest@Repeated[anyCaseWordPattern,2]~~propositionTypePattern]/;(Not@StringMatchQ[StringTrim[x],"The"|"A"|"Use",IgnoreCase->True])
]
]
]&,
(* Remove cases with useless words in them *)
Select[
With[
(* Ignore "of" so that case #3 is allowed *)
{split=DeleteCases[StringSplit[ToLowerCase[#],Whitespace|"-"],"of"]},
split===DeleteCases[DeleteStopwords[split],"using"|"like"|"phd"|"understanding"|"finally"|"concerning"|"regarding"|"ℳℋ"|""|"satisfies"|"following"|"stated"|"usually"|"implies"|"hence"|"course"|"assuming"|"wikipedia"|"article"|"usual"|"actually"|"analysis"|"entitled"|"apply"]
]&
],
StringReplace[Normal@$ordinalToWord],
lowerCaseSpecificWords,
StringTrim,
DeleteDuplicates,
Map[addPropositionEntity]
]
];
|
Let’s try the function on a simple example:
![["Body"] // extractNamedPropositions ["Body"] // extractNamedPropositions](https://content.wolfram.com/sites/39/2019/01/img23.png)
✕
Entity["StackExchange.Mathoverflow:Post", "40686"]["Body"]//extractNamedPropositions |
We can see that an entity was added to the store:

✕
EntityList["MathematicalProposition"][[-3;;]] |
We can also see that its properties were populated:

✕
Entity["MathematicalProposition", "MartinAxiom"]["PropertyAssociation"] |
Of course, we can automate this a bit more by introducing this function as a property for MathOverflow posts that will store the results in the EntityStore itself:

✕
EntityProperty["StackExchange.Mathoverflow:Post","NamedPropositions"]["Label"]="named propositions"; EntityProperty["StackExchange.Mathoverflow:Post","NamedPropositions"]["DefaultFunction"]=Function[entity,entity["NamedPropositions"]=extractNamedPropositions[entity["Body"]]]; |
Let’s test out the property on the same Entity as before:

✕
Entity["StackExchange.Mathoverflow:Post", "40686"]["NamedPropositions"] |
We can see that the in-memory store has been populated:
![Entity["MathematicalProposition"] Entity["MathematicalProposition"]](https://content.wolfram.com/sites/39/2019/01/7Janimg164.png)
✕
Entity["MathematicalProposition"]["EntityStore"] |
Pro tip: in case you want to continue to work on an EntityStore you’ve been modifying in-memory in a future Wolfram Language session, you can Export Entity["type"]["EntityStore"] to an MX file and then Import it in the new session. Just don’t forget to register it with EntityRegister!
At this point, we can now gather propositions mentioned in all of the MathOverflow posts, taking care to reset the counters again to avoid contamination of the results:
![#["MentionedPostCount"] #["MentionedPostCount"]](https://content.wolfram.com/sites/39/2019/01/7Janimg165.png)
✕
(* Reset counters again to avoid contaminating the results *) #["MentionedPostCount"]=0;&/@EntityList["MathematicalProposition"]; #["Wordings"]=Association[#["Label"]->1];&/@EntityList["MathematicalProposition"]; |
Note that this will take a while to run (it took about 20 minutes on my machine), but it will allow for a very thorough analysis of the site’s content.
After processing all of the posts, there are now over 10k entities in the proposition EntityStore:

✕
postToNamedPropositions=EntityValue["StackExchange.Mathoverflow:Post","NamedPropositions","EntityAssociation"]; |

✕
EntityValue["MathematicalProposition","Entities"]//Length |
Data Cleanliness
Having kept track of the wordings for each proposition was a good choice—now we can see that proposition entities will format with the most commonly used wording. For example, look at Stokes’ theorem:

✕
Entity["MathematicalProposition", "StokesTheorem"]["Wordings"] |
It’s named after George Gabriel Stokes, and so the correct possessive form ends in “s’,” not “’s,” despite about 15 percent of mentions using the incorrect form.
I’ll admit that this normalization is not perfect—when someone removes the first “s” altogether, it is picked up in a different entity:

✕
Entity["MathematicalProposition", "StokeTheorem"]["Wordings"] |
Rather than spend a lot of time and effort to normalize these small issues, I’ll move on and work around these problems for now.
Proposition Analysis
Now that we have a lot of data on the propositions mentioned in the post bodies, we can visualize the most commonly mentioned propositions in a word cloud:

✕
topPropositionToCount=ReverseSort@EntityValue[EntityClass["MathematicalProposition",{"MentionedPostCount"->TakeLargest[100]}],"MentionedPostCount","EntityAssociation"];
|

✕
WordCloud[topPropositionToCount[[;;20]],ImageSize->400,WordOrientation->{{π/4,-(π/4)}}]
|
It seems that the prime number theorem is the most commonly mentioned:
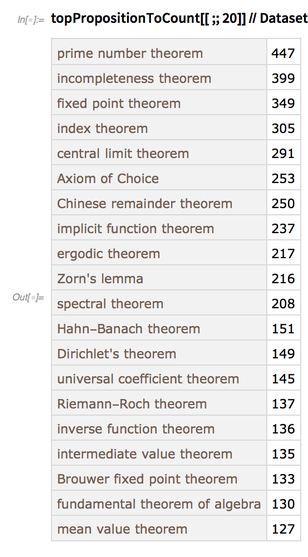
✕
topPropositionToCount[[;;20]]//Dataset |
We can also see that about two-thirds of all propositions are theorems:

✕
propositionTypeBreakdown=EntityValue["MathematicalProposition","PropositionType"]//Counts//ReverseSort |
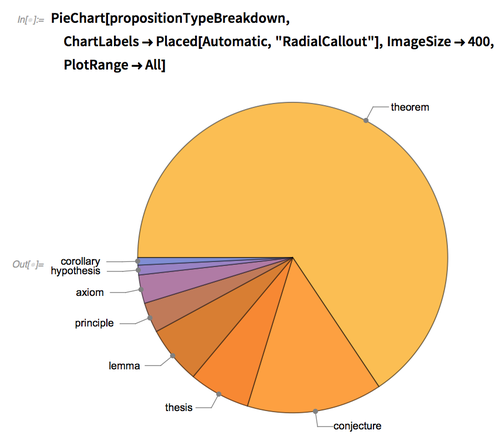
✕
PieChart[propositionTypeBreakdown,ChartLabels->Placed[Automatic,"RadialCallout"],ImageSize->400,PlotRange->All] |
Mathematicians
Now that we have the propositions, we can look for mathematician names in the propositions.
Build
To start, we can find all of the labels for the propositions:

✕
propositionToLabel=EntityValue["MathematicalProposition","Label","EntityAssociation"]; |
Next, we’ll need to find the words in the labels, drop proposition types and stopwords and count them up (taking care to not separate names that start with “de” or “von”):

✕
commonWordsInPropositions=propositionToLabel//RightComposition[
Values,
StringReplace[prefix:"Van der"|"de"|"De"|"von"|"Von"~~(Whitespace|"-")~~name:(_?UpperCaseQ~~LetterCharacter):>StringReplace[prefix,Whitespace->"_"]<>"_"<>name],
StringSplit/*Flatten/*DeleteStopwords,
Counts/*ReverseSort,
KeyDrop[Flatten@EntityValue[EntityClass["MathematicalPropositionType",All],{"CanonicalName","Label"}]]
];
|
Next, we can look for groups of mathematician names joined by dashes (taking care to remove words that are obviously not names):

✕
namePattern=((_?UpperCaseQ|("von"|"de"))~~(LetterCharacter|"_")..);
mathematiciansJoinedByDashes=Select[Keys[commonWordsInPropositions],StringMatchQ[namePattern~~Repeated["-"~~namePattern,{1,Infinity}]]]//StringSplit[#,"-"]&//Flatten//Union//StringReplace["_"->" "];
mathematiciansJoinedByDashes=DeleteCases[mathematiciansJoinedByDashes,"Anti"|"Foundation"|"Max"|"Flow"|"Min"|"Cut"];
mathematiciansJoinedByDashes//Length
|
Another source of names is possessive words, as in “Zorn’s lemma”:

✕
possesiveNames=Keys[commonWordsInPropositions]//Select[StringEndsQ["'s"|"s'"]]; possesiveNames//Length |
After some cleanup (e.g. removing inline ![]() snippets and references to the Clay Mathematics Institute’s Millennium Prize problems), most of these are likely last names for mathematicians:
snippets and references to the Clay Mathematics Institute’s Millennium Prize problems), most of these are likely last names for mathematicians:

✕
mathematicansByPossessives=StringTrim[possesiveNames,"'s"|"s'"]//RightComposition[ StringSplit[#,"-"]&, Flatten/*DeleteDuplicates, StringReplace["_"->" "], Select[StringMatchQ[#,_?UpperCaseQ~~(_?LowerCaseQ)~~___]&], Select[StringFreeQ["ℳℋ"]] ]; mathematicansByPossessives=DeleteCases[mathematicansByPossessives,"Clay"|"Millennium"]; mathematicansByPossessives//Length |
Combining these two lists should result in a fairly complete list of mathematician names:

✕
allMathematicians=Union[mathematiciansJoinedByDashes,mathematicansByPossessives]; allMathematicians//Length |
The results seem pretty decent:

✕
Multicolumn[RandomSample[allMathematicians,16]] |
Now we need to find possible ways to write down the names of each mathematician.
After looking through the data, I found a few cases that needed to be corrected manually. Specifically, a few names are written out for the famous Jacob Lurie and R. Ranga Rao, so they need to be corrected to clean up the results a bit:

✕
mathematicianToPossibleNames=GroupBy[allMathematicians,RemoveDiacritics/*StringReplace["_"->" "]/*toStandardName]; mathematicianToPossibleNames["Lurie"]=PrependTo[mathematicianToPossibleNames["Lurie"],"Jacob Lurie"]; mathematicianToPossibleNames["Ranga"]=PrependTo[mathematicianToPossibleNames["Ranga"],"Ranga Rao"]; |
Now, we need to construct an Association to point from individual name words to their mathematicians:

✕
possibleNameToMathematicians=mathematicianToPossibleNames//RightComposition[ KeyValueMap[Thread[Rule[##]]&], Flatten, GroupBy[Last->First], Map[Entity["Mathematician",#]&/@Flatten[#]&] ]; |
Note that these entities do not format—we’ll create the EntityStore for them soon:

✕
possibleNameToMathematicians[[;;10]] |
From here, we can break the proposition labels into words that we can use to look up mathematicians (taking care to fix a few cases that need special attention for full names written out):

✕
propositonToLabelWords=propositionToLabel//RightComposition[
Map[
StringReplace[prefix:("De"|"de"|"von"|"Von"|"Jacob"|"Alex"|"Yoon"|"Ranga")~~Whitespace|"-"~~name:(namePattern|"Ho"|"Lurie"|"Lee"|"Rao"):>prefix<>"_"<>name]/*(StringSplit[#,Whitespace|"-"]&)/*(StringTrim[#,"'s"|"s'"]&)/*StringReplace["_"->" "]
]
];
|

✕
propositionToMathematicians=DeleteDuplicates@Flatten@DeleteMissing@Lookup[possibleNameToMathematicians,#]&/@propositonToLabelWords; |
With this done, we can add this data to the proposition store as a new property:

✕
EntityProperty["MathematicalProposition","NamedMathematicians"]["Label"]="named mathematicians"; KeyValueMap[(#1["NamedMathematicians"]=#2)&,propositionToMathematicians]; |
And by rearranging the data, we can build the data to create an EntityStore for mathematicians:

✕
mathematicanToPropositions=propositionToMathematicians//RightComposition[ KeyValueMap[Thread[Rule[##]]&], Flatten, GroupBy[Last->First] ]; |

✕
KeyTake[mathematicanToPropositions,{Entity["Mathematician", "DeFinnetti"],Entity["Mathematician", "Lurie"],Entity["Mathematician", "Ranga"]}]
|
Populate
Using this data, we can now build an EntityStore for mathematicians, taking into account the data we’ve accumulated:

✕
mathematicanData=Association@KeyValueMap[ Rule[ #1, <| "Label"->First[#2], "PossibleNames"->#2, "NamedPropositions"->Lookup[mathematicanToPropositions,Entity["Mathematician",#1]] |> ]&, mathematicianToPossibleNames ]; |

✕
mathematicianStore=EntityStore[
{
"Mathematician"-><|
"Entities"->mathematicanData,
"Properties"-><|
"Label"-><|"Label"->"label"|>,
"PossibleNames"-><|"Label"->"possible names"|>,
"NamedPropositions"-><|"Label"->"named propositions"|>
|>
|>
}
];
EntityUnregister/@mathematicianStore[];
EntityRegister[mathematicianStore]
|
Now we can see the propositions named after a specific mathematician, such as Euler:

✕
EntityValue[Entity["Mathematician", "Euler"],"NamedPropositions"] |
Analysis
At this point, many interesting queries are possible.
As a start, let’s look at a network that connects two mathematicians if they appear in the same proposition name. It sounds somewhat similar to the Mathematics Genealogy Project.
An example might be the “Grothendieck–Tarski axiom”:

✕
Entity["MathematicalProposition", "GrothendieckTarskiAxiom"]["NamedMathematicians"] |
First, grab all of the named mathematicians for each proposition, taking only those that have at least two:

✕
groupedMathematicianData=Select[EntityValue["MathematicalProposition","NamedMathematicians","EntityAssociation"],Length[#]>=2&]; |

✕
groupedMathematicianData[[;;10]] |
With a little bit of analysis, we can see that the majority of propositions have two mathematicians, fewer have three, there are a few groups of four and there is only one group of five:

✕
groupedMathematicianData//Values//CountsBy[Length]//KeySort |
Here is the group of five, mentioned in this answer:

✕
TakeLargestBy[groupedMathematicianData,Length,1] |
Here are the top 25 results:
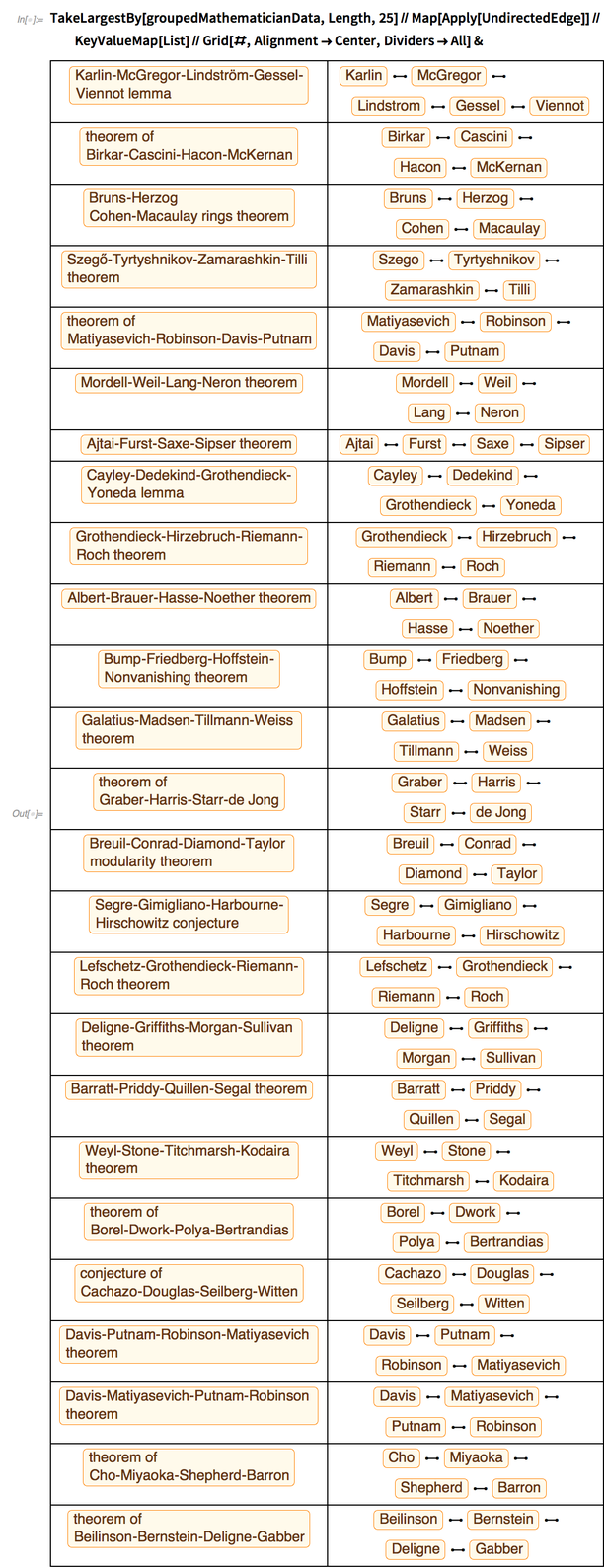
✕
TakeLargestBy[groupedMathematicianData,Length,25]//Map[Apply[UndirectedEdge]]//KeyValueMap[List]//Grid[#,Alignment->Center,Dividers->All]& |
We can complete our task by constructing a network of all grouped mathematicians:

✕
groupedMathematicianEdges=Flatten[(UndirectedEdge@@@Subsets[#,{2}])&/@Values[groupedMathematicianData]];
groupedMathematicianEdges//Length
|
The network is quite large and messy.
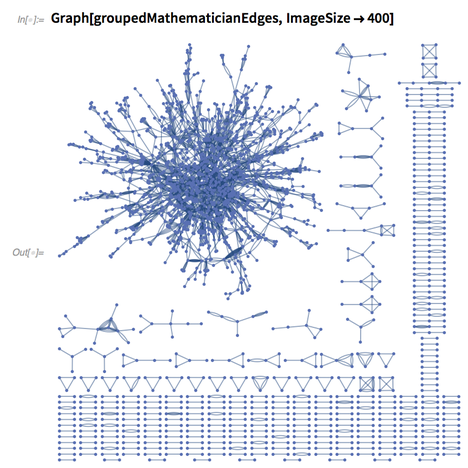
✕
Graph[groupedMathematicianEdges,ImageSize->400] |
With some more processing, we can add weights for repeated edges and use them to determine their opacity:
|
✕
weightedMathematicanEdges=ReverseSort[Counts[groupedMathematicianEdges]]; |
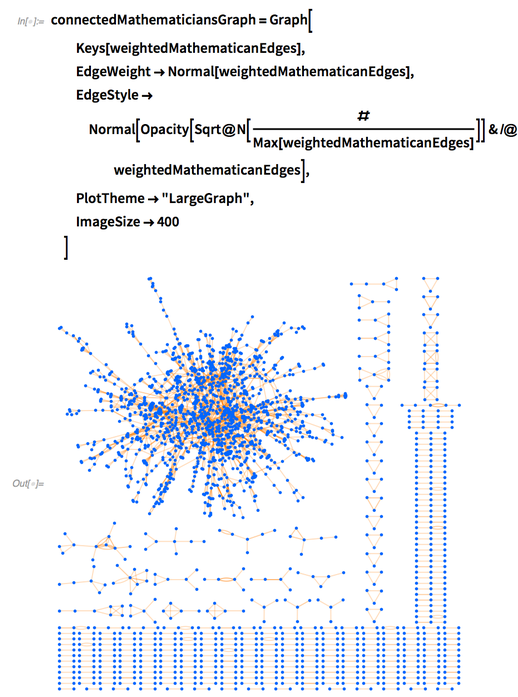
✕
connectedMathematiciansGraph=Graph[ Keys[weightedMathematicanEdges], EdgeWeight->Normal[weightedMathematicanEdges], EdgeStyle->Normal[Opacity[Sqrt@N[#/Max[weightedMathematicanEdges]]]&/@weightedMathematicanEdges], PlotTheme->"LargeGraph", ImageSize->400 ] |
Here are the most common pairings of mathematicians:

✕
weightedMathematicanEdges[[;;10]] |
And here’s an easy way to see who has the most propositions named after them, which can be done with SortedEntityClass, new in Mathematica 12:

✕
mathematicianToPropositions=EntityValue[ SortedEntityClass["Mathematician",EntityFunction[entity,Length[entity["NamedPropositions"]]]->"Descending"], "NamedPropositions", "EntityAssociation" ]; mathematicianToPropositions//Length |
Here are the top 25, along with the number of propositions in which they are mentioned on MathOverflow:

✕
Length/@mathematicianToPropositions[[;;25]] |
Despite his common appearance in theorems, Euler is surprisingly very low on this list at number 61:

✕
Position[Keys[mathematicianToPropositions],Entity["Mathematician", "Euler"]] |
And here’s the full distribution of mentions (on a log scale for easier viewing):
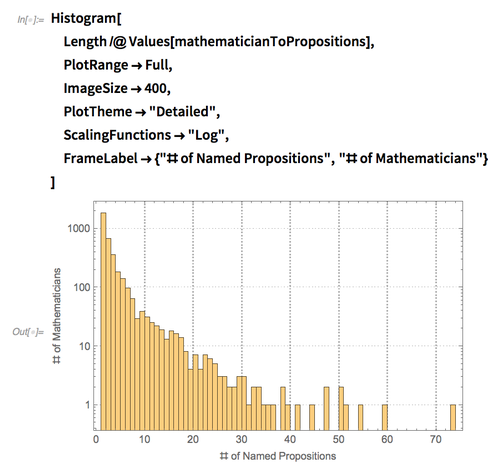
✕
Histogram[
Length/@Values[mathematicianToPropositions],
PlotRange->Full,
ImageSize->400,
PlotTheme->"Detailed",
ScalingFunctions->"Log",
FrameLabel->{"# of Named Propositions","# of Mathematicians"}
]
|
Do It Yourself
Be sure to explore further using the newest functions coming soon in Version 12 of the Wolfram Language!
Although I used a lot of Wolfram technology to explore the data on MathOverflow.net, here are some open areas that still remain to be explored:
- What fraction of all questions are unanswered?
- Which tags have the most answered or unanswered questions?
- Find named mathematical structures (e.g. integral, group, Riemann sum, etc.)
- Align entities to MathWorld for further investigation
- Investigate the time series ratio of user count to post count
In fact, you can download and register the entity stores used in this post here:
- Pre-generated, incomplete MathOverflow.net EntityStore
- Completed MathOverflow.net EntityStore
- Completed mathematical proposition EntityStore
- Completed mathematician EntityStore



Andrew
Thank you very much for providing such an interesting blog. A number of questions: Is it possible to get the notebook for this blog, rather than having to retype everything? Secondly how does this link in with the recent attempts by WRI and Eric from MathWorld to create an EntityStore on Algebraic Topology, which was covered in a number of WTC 2017 talks? Lastly, if it possible to create EntityStores from the Stack Exchange archives , is it also possible to create EntityStores on mathematical theorems from the corresponding Wikipedia articles using WikipediaSearch and WikipediaData ?
Thanks again for your blog and any responses to my questions
Michael
Thanks for reading! I’m glad you enjoyed it!
I am not familiar with the MathWorld EntityStore you’ve mentioned, but if anything, parts of this blog can used as a stepping stone to create your own EntityStores based on any data source.
Concerning EntityStores created from Wikipedia: I myself haven’t done this, but it sounds like an interesting project, and could probably be done without too much trouble. I’d be curious to see what results can be found from this data!
Well done Andrew!
Pretty impressive data processing functionalities of Version 12. I can’t wait to get a copy of it.
Love the wordsMuchMoreCommonInMO graphics.
(1) As useful to Mathematica users, perhaps, as MathOverflow.net, would be an entity store of https://mathematica.stackexchange.com.
(2) Is there a button somewhere that I’m missing to allow downloading this blog post as a notebook? Or at the very least, cause double clicking displayed code in this blog post to be copyable as text, so that it can be pasted into a notebook. Just having a bunch of .jpg’s showing code is very unhelpful!
Thanks for reading! I hope you enjoyed it!
(1) Yes, I have looked at and analyzed mathematica.stackexchange.com, as well as several other SE sites, and I have found some interesting things! I hope to do another blog post, and in particular, cover mathematica.stackexchange.com in greater detail in the near future.
(2) I certainly agree about the lack of a notebook and copyable code! Some functionality in the post requires the upcoming Version 12 (which, as of this writing, is unreleased). I didn’t want to give out the code as some would not work properly in older versions (e.g. the SPARQL query parts). Once Version 12 does is released, the notebook and copyable code will be available. Sorry for the inconvenience!
could we have https://gamedev.stackexchange.com as an entity store?
or maybe only https://gamedev.stackexchange.com/questions/tagged/unity
Thank you,
Hi Luc,
I made an EntityStore of gamedev.stackexchange.com with the current version of the utility and hosted it in the Wolfram Cloud.
You can get it with this WL code (it’s around 600 MB large):
gameDevSEStore = Import[CloudObject[“https://www.wolframcloud.com/objects/andrews/StackExchange2EntityStore/gamedev.stackexchange.com.mx”]];
Then, you can register it for use in EntityValue with this:
EntityRegister[gameDevSEStore]
The basic features in the store should still work in Mathematica 11.3, and I’ve made a notebook to show a few simple things I found in it, including all posts with the “unity” tag:
https://www.wolframcloud.com/objects/andrews/Published/gamedev.stackexchange.com
Let me know if you have any questions!
Thanks,
Andrew
Would be interesting to see if some statistics can be used to charactetize group/social dynamics at MO. I’d be particularly interested in seeing statistics of those who frequently vote to close questions. For example, it appears that some such voters actually ask few questions themselves or ask few highly favorited, or liked, or viewed questions. How are their statistics skewed from the general population of voters at given voting frequencies?