The upcoming August 21, 2017, total solar eclipse is a fascinating event in its own right. It’s also interesting to note that on April 8, 2024, there will be another total solar eclipse whose path will cut nearly perpendicular to the one this year.

With a bit of styling work and zooming in, you can see that the city of Carbondale, Illinois, is very close to this crossing point. If you live there, you will be able to see a total solar eclipse twice in only seven years.

Let’s aim for additional precision in our results and compute where the intersection of these two lines is. First, we request the two paths and remove the GeoPosition heads.

Then we can use RegionIntersection to find the intersection of the paths and convert the result to a GeoPosition.

By zooming in even further and getting rid of some of the style elements that are not useful at high zoom levels, we can try to pin down the crossing point of the two eclipse center paths.

It appears that the optimal place to be to see the longest eclipse for both locations would be just southwest of Carbondale, Illinois, near the east side of Cedar Lake along South Poplar Curve Road where it meets with Salem Road—although anywhere in the above image would see a total solar eclipse for both of the eclipses.

Because of this crossing point, I expect a lot of people will be planning to observe both the 2017 and 2024 solar eclipses. Don’t wait until the last minute to plan your trip!

So how often do eclipse paths intersect? We can find out with a little bit of data exploration. First, we need to get the dates, lines and types of all eclipses within a range of dates. Let’s limit ourselves to 40 years in the past to 40 years in the future for a total of about 80 years.

Keep only the eclipses for which path data is available.

Generate a set of all pairs of eclipses.

Now we define a function to test if a given pair of eclipse paths intersect.

Finally, we apply that function to all pairs of eclipses and keep only those for which an intersection occurs.

It turns out that there are a little over one hundred eclipses that intersect during this timespan.

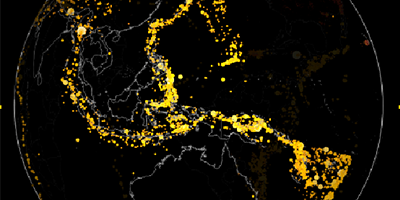
We can visualize the distribution of these eclipse paths to see that many occur over the oceans. The chances of an intersection being within driving distance of a given land location is far lower.

So take advantage of the 2017 and 2024 eclipses if you live near Carbondale, Illinois! It’s unlikely you will see such an occurrence anytime soon without making a lot more effort.